
Para dar um exemplo de análise de fatores usaremos o módulo factor_analyser do Python. Os dados usados são originados do Synthetic Aperture Personality Assessment (SAPA) que contém 25 questões de auto-avaliação pessoais disponíveis na web na página de Vincent Arel-Bundock, no Github.
A documentação do Factor Analyser pode ser lida nessa página.
SAPA e BFI
SAPA, Synthetic Aperture Personality Assessment, é um método usado para avaliar diferenças de personalidade individuais, muito utilizado para pesquisas online. O sujeito testado recebe um subconjunto aleatório dos itens em estudo com o objetivo de reunir grande volume de dados suficientes para a montagem de grandes matrizes de covariância (de relacionamento entre os dados verificados). O teste online foi desenvolvido por William Revelle e é mantido pela Northwestern University, Ilinois, EUA.
A1: Sou indiferente aos sentimentos das outras pessoas.
A2: Sempre pergunto sobre o bem-estar dos outros.
A3: Sei como confortar os outros.
A4: Adoro crianças.
A5: Faço as pessoas se sentirem à vontade.C1: Sou exigente no meu trabalho.
C2: Continuo minhas tarefas até que tudo esteja perfeito.
C3: Faço as coisas de acordo com um plano.
C4: Deixo tarefas semi-acabadas.
C5: Desperdiço meu tempo.E1: Não falo muito.
E2: Tenho dificuldades para abordar outras pessoas.
E3: Sei como cativar as pessoas.
E4: Faço amigos facilmente.
E5: Assumo o controle das situações.
N1: Fico com raiva facilmente.
N2: Irrito-me facilmente.
N3: Tenho alterações de humor frequentes.
N4: Muitas vezes me sinto triste.
N5: Entro em pânico facilmente.
O1: Sempre tenho muitas ideias.
O2: Evito leituras complexas.
O3: Procuro levar as conversas para um nível elevado.
O4: Passo algum tempo refletindo sobre as coisas.
O5: Nunca me detenho a avaliar um assunto profundamente.
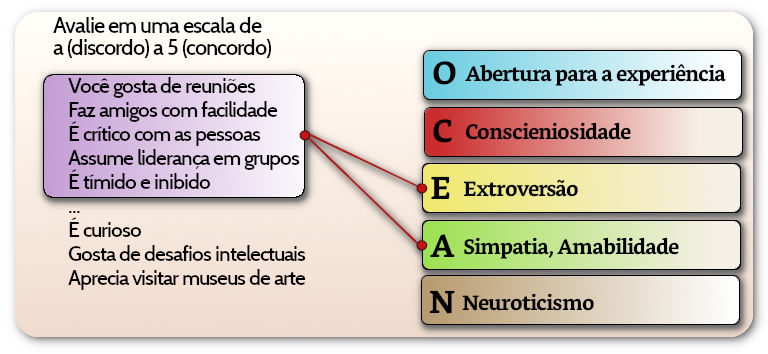
A escala usada para respostas usada foi:
1. Totalmente falso
2. Moderadamente falso
3. Um pouco falso
4. Um pouco correto
5. Moderadamente correto
6. Totalmente corretoIndicadores Demográficos:
estão codificados da seguinte forma:
Gênero:
1. Masculino,
2. Feminino.
Idade: a idade (em anos).
Educação:
1. Nível médio incompleto,
2. Nível médio completo,
3. Nível superior incompleto,
4. Nível superior completo,
5. Pós-graduação.Fatores esperados:
Os itens estão organizados por fatores esperados (a serem verificados pela análise):
Agreeableness, (Amabilidade),
Conscientiousness, (Conscienciosidade),
Extroversion, (Extroversão),
Neuroticism, (Neuroticismo) e
Opennness, (Abertura).
O arquivo de respostas disponível foi baixado como o nome bfi.csv e salvo na pasta do projeto, subpasta ./dbs. Esse arquivo contém dados no formato *.csv (valores separados por vírgula) relativos a 2800 sujeitos com 3 campos adicionais de dados demográficos: sexo, educação e idade.
Jupyter Notebook e convenções usadas

Jupyter Notebook é uma aplicação web e opensource que permite sessões colaborativas e documentos compartilhados contendo código que pode ser executado dentro da página, equações bem formatadas, visualização gráfica e texto narrativo que podem ser postas sob forma de apresentações ou usadas para desenvolvimento. Seu uso inclui tratamento, transformação e visualização de dados, simulações numéricas, modelagem estatística, machine learning entre outras aplicações.
O projeto será rodado em uma sessão do Jupyter Notebook. Nessa página usamos as seguintes convenções: células de código do Jupyter Notebook aparecem dentro de caixas como a exibida abaixo. Nos notebooks (como no Python) linhas iniciadas pelo sinal “#” são comentários. Apenas nessas páginas outputs simples e compactos podem aparecer como um comentário após o comando como mostrado abaixo (diferente do que ocorre nos notebooks). Outpus mais complexos aparecem em caixas separadas.
# Exemplo de exibição das células do Jupyter Notebook.
print('output simples') # Esse comando imprime 'output simples'
# Outpus mais complexos aparecem em caixas separadas:
print('Outputs do Jupyter Notebook, gráficos e dataframes exibidos aparecem como nesse quadro...')
Módulo Factor Analyser
Factor Analyser é um módulo desenvolvido em Python por Jeremy Biggs e Nitin Madnani, publicado em 2017 para realizar análise fatorial exploratória e confirmatória (AFE, AFC). As classes do pacote são compatíveis com a biblioteca scikit-learn. Partes do código são portadas da biblioteca psych do R.
Tratamento dos dados do bsi por meio do factor_analyser
Instalamos o módulo factor_analyzer dentro do Jupyter Notebook. Em seguida importamos as bibliotecas necessárias: além do próprio factor_analyzer usamos o pandas e numpy para as manipelações de dados e matplotlib para as visualizações.
# Instalação do factor_analyzer:
conda install -c ets factor_analyzer
# Importando bibliotecas (libraries) necessárias
import pandas as pd
import numpy as np
from factor_analyzer import FactorAnalyzer
import matplotlib.pyplot as plt
# A leitura do arquivo de dados para dentro de um dataframe (do pandas)
df = pd.read_csv('./dbs/bfi.csv')
# Renomear a primeira coluna (que está sem nome) para 'id'
df.rename(columns = {'Unnamed: 0':'id'}, inplace = True)
print('A tabela importada contém %d linhas, %d colunas' % df.shape)
print('contendo as seguintes colunas:\n', df.columns)
# Para visualizar a tabela importada:
df.head()
contendo as seguintes colunas:
Index([‘id’, ‘A1’, ‘A2’, ‘A3’, ‘A4’, ‘A5’, ‘C1’, ‘C2’, ‘C3’, ‘C4’, ‘C5’, ‘E1’,
‘E2’, ‘E3’, ‘E4’, ‘E5’, ‘N1’, ‘N2’, ‘N3’, ‘N4’, ‘N5’, ‘O1’, ‘O2’, ‘O3’,
‘O4’, ‘O5’, ‘gender’, ‘education’, ‘age’],
dtype=’object’)
| id | A1 | A2 | A3 | A4 | A5 | C1 | C2 | C3 | C4 | … | N4 | N5 | O1 | O2 | O3 | O4 | O5 | gender | education | age | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 61617 | 2.0 | 4.0 | 3.0 | 4.0 | 4.0 | 2.0 | 3.0 | 3.0 | 4.0 | … | 2.0 | 3.0 | 3.0 | 6 | 3.0 | 4.0 | 3.0 | 1 | NaN | 16 |
| 1 | 61618 | 2.0 | 4.0 | 5.0 | 2.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | … | 5.0 | 5.0 | 4.0 | 2 | 4.0 | 3.0 | 3.0 | 2 | NaN | 18 |
| 2 | 61620 | 5.0 | 4.0 | 5.0 | 4.0 | 4.0 | 4.0 | 5.0 | 4.0 | 2.0 | … | 2.0 | 3.0 | 4.0 | 2 | 5.0 | 5.0 | 2.0 | 2 | NaN | 17 |
| 3 | 61621 | 4.0 | 4.0 | 6.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | 5.0 | … | 4.0 | 1.0 | 3.0 | 3 | 4.0 | 3.0 | 5.0 | 2 | NaN | 17 |
| 4 | 61622 | 2.0 | 3.0 | 3.0 | 4.0 | 5.0 | 4.0 | 4.0 | 5.0 | 3.0 | … | 4.0 | 3.0 | 3.0 | 3 | 4.0 | 3.0 | 3.0 | 1 | NaN | 17 |
2800 rows × 29 columns
Como em qualquer outro uso de dados, principalmente quando importados de fontes externas, fazemos uma verificação de estrutura e completeza ou a existência de valores ausentes (NaN). Os dados demográficos são armazendos em outro dataframe enquanto a avaliação das questões em si são deixadas no dataframe df depois de eliminados os campos relativos a dados demográficos.
# Tabela dfDemografico armazena id, sexo, educação e idade dfDemografico = df[['id', 'gender', 'education', 'age']] # Colunas desnecessárias são eliminadas de df df.drop(['id', 'gender', 'education', 'age'],axis=1,inplace=True) # Possíveis dados ausentes são eliminados df.dropna(inplace=True) # Para verificar as colunas de df df.head(2)
| A1 | A2 | A3 | A4 | A5 | C1 | C2 | C3 | C4 | C5 | … | N1 | N2 | N3 | N4 | N5 | O1 | O2 | O3 | O4 | O5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2.0 | 4.0 | 3.0 | 4.0 | 4.0 | 2.0 | 3.0 | 3.0 | 4.0 | 4.0 | … | 3.0 | 4.0 | 2.0 | 2.0 | 3.0 | 3.0 | 6 | 3.0 | 4.0 | 3.0 |
| 1 | 2.0 | 4.0 | 5.0 | 2.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | 4.0 | … | 3.0 | 3.0 | 3.0 | 5.0 | 5.0 | 4.0 | 2 | 4.0 | 3.0 | 3.0 |
2 rows × 25 columns
# Uma visão geral dos dados no dataframe df pode ser vista: df.info()
Int64Index: 2436 entries, 0 to 2799
Data columns (total 25 columns):
# Column Non-Null Count Dtype
—————————————————————————————
0 A1 2436 non-null float64
1 A2 2436 non-null float64
2 A3 2436 non-null float64
3 A4 2436 non-null float64
4 A5 2436 non-null float64
… Grupos C, E, N omitidos
20 O1 2436 non-null float64
21 O2 2436 non-null int64
22 O3 2436 non-null float64
23 O4 2436 non-null float64
24 O5 2436 non-null float64
dtypes: float64(24), int64(1)
memory usage: 494.8 KB
Observamos que apenas o campo O2 tem tipo de variável int64. Apenas para ter todos os campos do mesmo tipo fazemos a conversão para float64.
# Converter o campo O2 em float df['O2'] = df['O2'].astype(np.float64) type(df['O2'][0]) # Agora o campo é do tipo numpy.float64
Considerando que em operações que faremos podemos perder o nome das colunas, vamos armazenar esses nomes em uma varável (que nesse caso é uma série).
itens=df.columns print(itens)
‘E3’, ‘E4’, ‘E5’, ‘N1’, ‘N2’, ‘N3’, ‘N4’, ‘N5’, ‘O1’, ‘O2’, ‘O3’, ‘O4’,
‘O5′],
dtype=’object’)
Matriz de Correlação

Estamos prontos para encontrar a matriz de correlação entre as variáveis. Cada célula dessa matriz mostra a correlação entre duas variáveis, listadas como labels das linhas e colunas. Por isso ele tem os valores da diagonal iguais a 1 (que é a correlação da variável consigo mesma). A matriz de correlação fornece uma visão geral de interrelacionamento dos dados e é usada como input para análises mais advançadas.
A correlação .corr é um método de dataframes do pandas. Por default o método corr usa os coeficientes de Pearson mas também pode usar os coeficientes Tau de Kendall ou coefficientes de Spearman.
# A matriz de correlação entre todas as respostas na tabela corrMatriz = df.corr() # Para ver apenas as correlações entre variáveis do grupo A corrMatriz[["A1", "A2","A3", "A4","A5"]].head(5)
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| A1 | 1.000000 | -0.350905 | -0.273636 | -0.156754 | -0.192698 |
| A2 | -0.350905 | 1.000000 | 0.503041 | 0.350856 | 0.397400 |
| A3 | -0.273636 | 0.503041 | 1.000000 | 0.384918 | 0.515679 |
| A4 | -0.156754 | 0.350856 | 0.384918 | 1.000000 | 0.325644 |
| A5 | -0.192698 | 0.397400 | 0.515679 | 0.325644 | 1.000000 |
Em seguida fazemos o gráfico de calor (heatmap) da matriz de correlação. Usamos a biblioteca seaborn para isso. Um heatmap associa uma cor a cada valor na matriz de correção. Tons mais escuros de azul (nesse caso) são valores mais perto de 1, tons mais claros são valores mais perto de -1.
import seaborn as sns
plt.figure(figsize=(12,12))
sns.set(font_scale=1)
sns.heatmap(corrMatriz, linewidths=.1, linecolor='#ffffff',
cmap='YlGnBu', xticklabels=1, yticklabels=1)
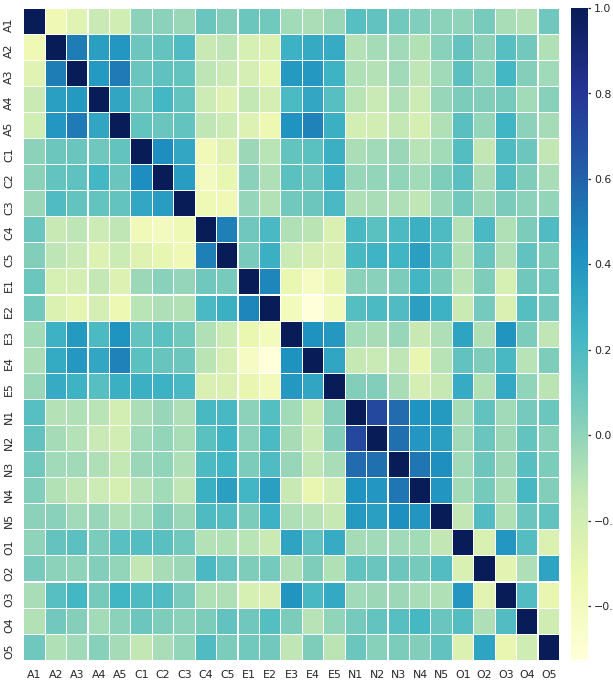

A mera análise do gráfico de calor permite que algumas características da pesquisa sejam visualmente reconhecidas. Duas variáveis diferentes com índice de correlação muito alto podem ser, na verdade, a mesma variável escrita de forma diversa. Nesse caso o pesquisador pode preferir retirar uma delas. Uma ou mais variáveis com nível de correlação muito baixo com todas as demais podem indicar a medida de elementos isolados e fora de contexto com o modelo explorado. Nesse caso vemos agrupamentos claros entre as variáveis A2, A3, A4, A5 e todas as do grupo N, só para citar alguns exemplos.
Análise Fatorial
Análise Fatorial Exploratória, AFE
Podemos agora dar início ao uso específico da Análise Fatorial, começando pela Análise Fatorial Exploratória, AFE, usando o módulo factor_analyzer. O primeiro passo para isso é a avaliação da fatorabilidade dos dados. Isso significa que os dados coletados podem ser agrupados em fatores, que são as nossas variáveis ocultas com o poder de sintetizar e melhor descrever o objeto estudado. Para isso o módulo factor_analyzer oferece dois testes: o Teste de Bartlett e o Teste de Kaiser-Meyer-Olkin.
Teste da esfericidade de Bartlett
O Teste da esfericidade de Bartlett verifica se as variáveis estão correlacionadas entre si, comparando a matriz de correlação com a matriz identidade (que representaria variáveis completamente não correlacionadas).
# Importa o módulo que realiza o teste de Bartlett
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
chi_square_value, p_value = calculate_bartlett_sphericity(df)
print('Teste da Esfericidade de Bartlett: chi² = %d, p_value = %d' % (chi_square_value, p_value))
No nosso caso o teste de Bartlett resulta em p-value = 0, o que indica que os dados podem ser fatorados e a matriz de correlação observada não é a identidade.
Teste de Kaiser-Meyer-Olkin
O Teste de Kaiser-Meyer-Olkin (KMO) fornece uma técnica de avaliação se os dados colhidos são apropriados para esta análise fatorial. Ele realiza um teste para cada variável observada e para o conjunto completo de variáveis. O resultado representa o grau em que cada variável observada pode ser predita, sem erros, pelas demais variáveis no conjunto de dados. KMO é uma estimativa da proporção de variância entre todas as variáveis. Os valores de KMO podem estar entre 0 e 1 e valores abaixo de 0.6 são consideredos inadequados.
# Importa calculate_kmo
from factor_analyzer.factor_analyzer import calculate_kmo
kmo_all,kmo_model = calculate_kmo(df)
print('Valores de kmo_all =\n', kmo_all, '\n')
print('KMO =', kmo_model)
[0.75391928 0.8363196 0.87010963 0.87795367 0.90348747 0.84325413
0.79568263 0.85186857 0.82647206 0.86401687 0.83801873 0.88380544
0.89697008 0.87731273 0.89332158 0.77933902 0.78025018 0.86229919
0.88518467 0.86014155 0.85858672 0.78019798 0.84434957 0.77003158
0.76144469]KMO = 0.848539722194922
Todos os valores de kmo_all são superiores a 0,7 e o KMO geral é KMO = 0.8485 o que são considerados valores muito favoráveis para a análise dos fatores.
Prosseguimos criando uma instância do objeto factor_analysis, tentativamente com 5 fatores
# Criamos objeto factor_analysis, sem rotação e usando 5 fatores (tentativamente)
fa = FactorAnalyzer(5, rotation=None)
# Aplicamos o método fit (ajuste) desse objeto no dataframe
fa.fit(df)
# Depois desse ajuste podemos coletar os autovetores e autovalores
ev, v = fa.get_eigenvalues()
print('São ' + str(len(ev)) + ' autovalores:\n', ev)
[5.13431118 2.75188667 2.14270195 1.85232761 1.54816285 1.07358247
0.83953893 0.79920618 0.71898919 0.68808879 0.67637336 0.65179984
0.62325295 0.59656284 0.56309083 0.54330533 0.51451752 0.49450315
0.48263952 0.448921 0.42336611 0.40067145 0.38780448 0.38185679
0.26253902]
Usando os autovalores calculados traçamos um Screeplot que é um gráfico que lista os autovalores em ordem decrescente, usado para determinar o número de fatores a serem retidos em uma análise fatorial exploratória. O teste, introduzido por R.B. Cattell em 1966, sugere manter tantos fatores quantos forem as autovalores anteriores a uma “dobra mais acentuada” ou “cotovelo” no gráfico. Também é sugerido manter o mesmo número de fatores quantos autovalores existirem maiores que 1.
from bokeh.plotting import figure, output_notebook, show
output_notebook()
eixoX = range(1, len(ev)+1) # de 1 0 26
eixoY = ev
p = figure(title="Scree Plot", x_axis_label='n-ésimo autovalor',y_axis_label='autovalor',
x_range=[0,25], y_range=(0, 6), plot_width=600, plot_height=400,
background_fill_color="#c9b2dd")
p.line(eixoX, eixoY, line_width=1, color = 'black')
p.circle(eixoX, eixoY, size=8, fill_color='red', color="black")
show(p)
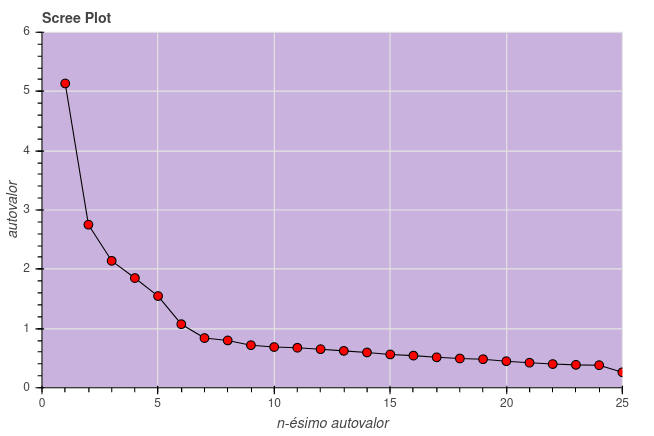
Algumas críticas são dirigidas ao teste feito dessa forma pois ele insere uma decisão pouco objetiva. Mais de um cotovelo podem aparecer no gráfico. De qualquer forma, como veremos no presente caso, o bom senso e a análise posterior dos agrupamentos de fatores podem sugerir uma alteração nesse número.
Cargas Fatoriais (factor loadings)
A carga fatorial é o coeficiente de correlação entre a variável e o fator. Ela mostra a variância explicada pela variável naquele fator em particular.
Prosseguimos criando um objeto FactorAnalyzer com 6 fatores (tentativamente) e usando o método de rotação varimax.
# 6 fatores fa = FactorAnalyzer( 6, rotation="varimax") # o objeto tem o método fit para análise do dataframe fa.fit(df) # Desse extraimos as cargas fatoriais (factor loadings) # Observe que fa.loadings_ é um numpy.array com shape (25,6). Usamos o método # do pandas pd.DataFrame.from_records para convertê-lo em um dataframe factorLoadings = pd.DataFrame.from_records(fa.loadings_) # Para ver a dataframe gerado: factorLoadings.head(4)
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0.095220 | 0.040783 | 0.048734 | -0.530987 | -0.113057 | 0.161216 |
| 1 | 0.033131 | 0.235538 | 0.133714 | 0.661141 | 0.063734 | -0.006244 |
| 2 | -0.009621 | 0.343008 | 0.121353 | 0.605933 | 0.033990 | 0.160106 |
| 3 | -0.081518 | 0.219717 | 0.235140 | 0.404594 | -0.125338 | 0.086356 |
Vemos que os nomes dos itens, de A1 até O5, foram perdidos no cálculo. Vamos renomear tanto esses itens quanto os nomes das colunas (que são os fatores) para ter uma visualização mais clara do que obtivemos até aqui:
# Substitue as linhas pelo nomes dos itens
factorLoadings.index=itens
# Renomeia as colunas
factorLoadings.rename(columns = {0:'Fator 1',
1:'Fator 2',
2:'Fator 3',
3:'Fator 4',
4:'Fator 5',
5:'Fator 6'}, inplace = True)
# Exibe o resultado
factorLoadings
| Fator 1 | Fator 2 | Fator 3 | Fator 4 | Fator 5 | Fator 6 | |
|---|---|---|---|---|---|---|
| A1 | 0.095220 | 0.040783 | 0.048734 | -0.530987 | -0.113057 | 0.161216 |
| A2 | 0.033131 | 0.235538 | 0.133714 | 0.661141 | 0.063734 | -0.006244 |
| A3 | -0.009621 | 0.343008 | 0.121353 | 0.605933 | 0.033990 | 0.160106 |
| A4 | -0.081518 | 0.219717 | 0.235140 | 0.404594 | -0.125338 | 0.086356 |
| A5 | -0.149616 | 0.414458 | 0.106382 | 0.469698 | 0.030977 | 0.236519 |
| C1 | -0.004358 | 0.077248 | 0.554582 | 0.007511 | 0.190124 | 0.095035 |
| C2 | 0.068330 | 0.038370 | 0.674545 | 0.057055 | 0.087593 | 0.152775 |
| C3 | -0.039994 | 0.031867 | 0.551164 | 0.101282 | -0.011338 | 0.008996 |
| C4 | 0.216283 | -0.066241 | -0.638475 | -0.102617 | -0.143846 | 0.318359 |
| C5 | 0.284187 | -0.180812 | -0.544838 | -0.059955 | 0.025837 | 0.132423 |
| E1 | 0.022280 | -0.590451 | 0.053915 | -0.130851 | -0.071205 | 0.156583 |
| E2 | 0.233624 | -0.684578 | -0.088497 | -0.116716 | -0.045561 | 0.115065 |
| E3 | -0.000895 | 0.556774 | 0.103390 | 0.179396 | 0.241180 | 0.267291 |
| E4 | -0.136788 | 0.658395 | 0.113798 | 0.241143 | -0.107808 | 0.158513 |
| E5 | 0.034490 | 0.507535 | 0.309813 | 0.078804 | 0.200821 | 0.008747 |
| N1 | 0.805806 | 0.068011 | -0.051264 | -0.174849 | -0.074977 | -0.096266 |
| N2 | 0.789832 | 0.022958 | -0.037477 | -0.141134 | 0.006726 | -0.139823 |
| N3 | 0.725081 | -0.065687 | -0.059039 | -0.019184 | -0.010664 | 0.062495 |
| N4 | 0.578319 | -0.345072 | -0.162174 | 0.000403 | 0.062916 | 0.147551 |
| N5 | 0.523097 | -0.161675 | -0.025305 | 0.090125 | -0.161892 | 0.120049 |
| O1 | -0.020004 | 0.225339 | 0.133201 | 0.005178 | 0.479477 | 0.218690 |
| O2 | 0.156230 | -0.001982 | -0.086047 | 0.043989 | -0.496640 | 0.134693 |
| O3 | 0.011851 | 0.325954 | 0.093880 | 0.076642 | 0.566128 | 0.210777 |
| O4 | 0.207281 | -0.177746 | -0.005671 | 0.133656 | 0.349227 | 0.178068 |
| O5 | 0.063234 | -0.014221 | -0.047059 | -0.057561 | -0.576743 | 0.135936 |
Vamos montar mais um heatmap com essa tabela.
# A bibioteca seaborn já foi importada como sns plt.figure(figsize=(8,6)) sns.set(font_scale=.9) sns.heatmap(factorLoadings, linewidths=1, linecolor='#ffffff', cmap="YlGnBu", xticklabels=1, yticklabels=1)
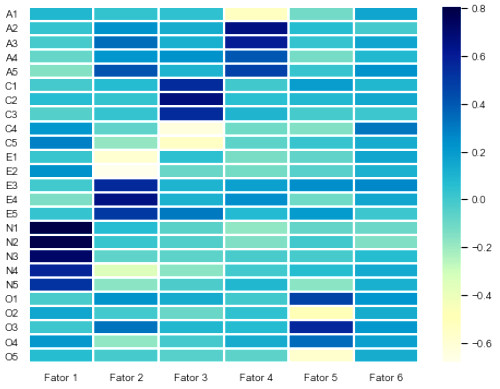
Lembrando que as cores mais escuras indicam correlação direta e as mais claras correlação inversa, percebemos que existem cargas mais fortes entre os itens N1, N2, N3, N4 e N5 com o fator 1, E1 até E5 no fator 2, etc. Nenhum dos itens, no entanto, tem carga relevante no sexto fator. Isso indica que podemos refazer o cálculo de cargas fatoriais com apenas 5 fatores.
# Refazendo o cáculo com 5 fatores apenas
# Apaga a variável fa
del fa
fa = FactorAnalyzer( 5, rotation="varimax")
fa.fit(df)
factorLoadings = pd.DataFrame.from_records(fa.loadings_)
# Renomeia itens
factorLoadings.index=itens
# Renomeia as colunas (fatores)
factorLoadings.rename(columns = {0:'Fator 1',
1:'Fator 2',
2:'Fator 3',
3:'Fator 4',
4:'Fator 5'}, inplace = True)
# Exibe o resultado
factorLoadings
| Fator 1 | Fator 2 | Fator 3 | Fator 4 | Fator 5 | |
|---|---|---|---|---|---|
| A1 | 0.111126 | 0.040465 | 0.022798 | -0.428166 | -0.077931 |
| A2 | 0.029588 | 0.213716 | 0.139037 | 0.626946 | 0.062139 |
| A3 | 0.009357 | 0.317848 | 0.109331 | 0.650743 | 0.056196 |
| A4 | -0.066476 | 0.204566 | 0.230584 | 0.435624 | -0.112700 |
| A5 | -0.122113 | 0.393034 | 0.087869 | 0.537087 | 0.066708 |
| C1 | 0.010416 | 0.070184 | 0.545824 | 0.038878 | 0.209584 |
| C2 | 0.089574 | 0.033270 | 0.648731 | 0.102782 | 0.115434 |
| C3 | -0.030855 | 0.023907 | 0.557036 | 0.111578 | -0.005183 |
| C4 | 0.240410 | -0.064984 | -0.633806 | -0.037498 | -0.107535 |
| C5 | 0.290318 | -0.176395 | -0.562467 | -0.047525 | 0.036822 |
| E1 | 0.042819 | -0.574835 | 0.033144 | -0.104813 | -0.058795 |
| E2 | 0.244743 | -0.678731 | -0.102483 | -0.112517 | -0.042010 |
| E3 | 0.024180 | 0.536816 | 0.083010 | 0.257906 | 0.280877 |
| E4 | -0.115614 | 0.646833 | 0.102023 | 0.306101 | -0.073422 |
| E5 | 0.036145 | 0.504069 | 0.312899 | 0.090354 | 0.213739 |
| N1 | 0.786807 | 0.078923 | -0.045997 | -0.216363 | -0.084704 |
| N2 | 0.754109 | 0.027301 | -0.030568 | -0.193744 | -0.010304 |
| N3 | 0.731721 | -0.061430 | -0.067084 | -0.027712 | -0.004217 |
| N4 | 0.590602 | -0.345388 | -0.178902 | 0.005886 | 0.075225 |
| N5 | 0.537858 | -0.161291 | -0.037309 | 0.100931 | -0.149769 |
| O1 | -0.002224 | 0.213005 | 0.115080 | 0.061550 | 0.504907 |
| O2 | 0.175788 | 0.004560 | -0.099729 | 0.081809 | -0.468925 |
| O3 | 0.026736 | 0.310956 | 0.076873 | 0.126889 | 0.596007 |
| O4 | 0.220582 | -0.191196 | -0.021906 | 0.155475 | 0.369012 |
| O5 | 0.085401 | -0.005347 | -0.062730 | -0.010384 | -0.533778 |
Construimos o heatmap com essa tabela de 5 fatores.
plt.figure(figsize=(8,6)) sns.set(font_scale=.9) sns.heatmap(factorLoadings, linewidths=1, linecolor='#ffffff', cmap="YlGnBu", xticklabels=1, yticklabels=1)
preta indicando grupos
de correlação foram
acrescentados manualmente.

Pelo heatmap percebemos que o grupo de itens N está associado ao fator 1 (Neuroticismo), E ao fator 2 (Extroversão), C ao fator 3 (Conscienciosidade), A ao fator 4 (Amabilidade) e O ao fator 5 (Abertura), previamente identificados. É claro que essa identificação do fator foi realizada pelos pesquisadores no caso dessa pesquisa em particular. Para uma pesquisa nova seria necessário um estudo para o entendimento da natureza de cada fator.
Observe ainda que correlação negativa é correlação. É o que ocorre, por exemplo entre os itens A1 (Sou indiferente aos sentimentos das outras pessoas) e A2 (Sempre pergunto sobre o bem-estar dos outros). A correlação entre eles pode ser obtida da matriz de correlação, corrMatriz['A1']['A2'] = -0.35091.
Observamos que existem as seguintes correspondências entre os grupos de questões e os fatores propostos:
| Fator | Grupo | Descrição |
|---|---|---|
| 1 | N | Neuroticismo |
| 2 | E | Extroversão |
| 3 | C | Conscienciosidade |
| 4 | A | Amabilidade |
| 5 | O | Abertura |
Vamos, portanto, renomear as colunas de nossa matriz de cargas fatoriais para refletir esse entendimento:
# Renomeia as colunas (fatores)
factorLoadings.rename(columns = {'Fator 1':'Neuroticismo',
'Fator 2':'Extroversão',
'Fator 3':'Conscienciosidade',
'Fator 4':'Amabilidade',
'Fator 5':'Abertura'}, inplace = True)
# Exibe o resultado (só duas linhas)
factorLoadings.head(2)
| Neuroticismo | Extroversão | Conscienciosidade | Amabilidade | Abertura | |
|---|---|---|---|---|---|
| A1 | 0.111126 | 0.040465 | 0.022798 | -0.428166 | -0.077931 |
| A2 | 0.029588 | 0.213716 | 0.139037 | 0.626946 | 0.062139 |
Comunalidades
Comunalidades são a soma das cargas fatoriais ao quadrado de cada variável medida. Denotando por \(l_{ij}\) os elementos da matriz da cargas fatoriais a comunalidade da i-ésima variável é \(h_i^2\) dado por
$$
h_i^2 =\Sigma_{j=1}^n l_{ij}^2
$$
Por exemplo, a comunalidade relativa à questão A1 é a soma dos elementos (ao quadrado) da primeira linha da matriz de cargas fatoriais acima:
(0.111126)**2 + (0.040465)**2 + (0.022798)**2 + (-0.428166)**2 +(-0.077931)**2
As comunalidades relativas a todas as variáveis podem ser obtidas com get_communalities() que retorna um numpy.ndarray com dimensões (25,):
fa.get_communalities()
0.34839471, 0.45387181, 0.32428892, 0.47669926, 0.43538283,
0.34780933, 0.545502 , 0.44105495, 0.54125654, 0.40714621,
0.68139838, 0.60800298, 0.54447487, 0.50580328, 0.34931564,
0.31733902, 0.26745151, 0.47464268, 0.2460347 , 0.29628368])
A soma de todos os valores de comunalidade é o valor de comunalidade total:
fa.get_communalities().sum()
Para exibir uma tabela com os nomes da variáveis e suas respectivas comunalidades vamos construir um dataframe contendo esses dados. Lembrando que já temos a variável itens = ['A1', 'A2', ..., 'O4','O5']:
dfComunalidades = pd.DataFrame(comunalidades) dfComunalidades.index = itens
| Variável | Comunalidade |
|---|---|
| A1 | 0.203905 |
| A2 | 0.462803 |
| A3 | 0.539692 |
| A4 | 0.301905 |
| A5 | 0.470020 |
| C1 | 0.348395 |
| C2 | 0.453872 |
| C3 | 0.324289 |
| C4 | 0.476699 |
| C5 | 0.435383 |
| Variável | Comunalidade |
|---|---|
| E1 | 0.347809 |
| E2 | 0.545502 |
| E3 | 0.441055 |
| E4 | 0.541257 |
| E5 | 0.407146 |
| N1 | 0.681398 |
| N2 | 0.608003 |
| N3 | 0.544475 |
| N4 | 0.505803 |
| N5 | 0.349316 |
| Variável | Comunalidade |
|---|---|
| O1 | 0.317339 |
| O2 | 0.267452 |
| O3 | 0.474643 |
| O4 | 0.246035 |
| O5 | 0.296284 |
| Total | 10.5905 |
| Como temos 25 fatores: | |
| Total/25 | 0.4236 |
Podemos pensar na comunalidade de uma variável como a proporção de variação nessa variável explicada pelos fatores propostos no modelo. Por exemplo, a variável N1 tem a maior comunalidade (0.681398) nesse modelo, indicando que aproximadamente 69% da variação nas respostas para “N1: Fico com raiva facilmente” é explicada pelo modelo de 5 fatores proposto enquanto esse valor é de apenas 20% para “A1: Sou indiferente aos sentimentos das outras pessoas”.
Comunalidades servem para avaliar o desempenho do modelo. Valores mais próximos de um indicam que o modelo explica a maior parte da variação para essas variáveis. Nesse caso o modelo está melhor ajustado para as variáveis do grupo N (neuroticismo) e menos eficiente para as variáveis do grupo O (abertura).
A Comunalidade total é de 10.5905 que, dividido entre as 25 variáveis indica uma média de 10.5905/25 = 0.4236 geral para o modelo, ou seja, uma eficiência média de 42% do modelo em explicar a variação de cada variável do teste.
Bibliografia
- Goldberg, L. R.: A broad-bandwidth, public domain, personality inventory measuring the lower-level facets of several five-factor models. In I. Mervielde, I. Deary, F. De Fruyt, & F. Ostendorf (Eds.), Personality Psychology in Europe, Vol. 7 (pp. 7-28). Tilburg, The Netherlands: Tilburg University Press, 1999.
- Biggs, Jeremy: Factor Analyser Documentation, acessado em dezembro de 2020.
- Site Datacamp: Navlani, Avinash: Introduction to Factor Analysis in Python, abril de 2019, acessado em dezembro de 2020.






















 Em 1961 Frank Drake, um dos entusiastas do projeto SETI, sugeriu uma equação que resume os principais conceitos envolvidos na possibilidade de se encontrar uma civilização extraterrestre usando comunicação por ondas eletromagnéticas. Ela não é a representação de nenhum modelo sério de estudo mas uma tentativa de estimação probabilística da existência dessas civilizações. Drake não procurava alcançar um número preciso mas sim uma forma de estimular o diálogo científico sobre a busca por inteligência extraterrestre.
Em 1961 Frank Drake, um dos entusiastas do projeto SETI, sugeriu uma equação que resume os principais conceitos envolvidos na possibilidade de se encontrar uma civilização extraterrestre usando comunicação por ondas eletromagnéticas. Ela não é a representação de nenhum modelo sério de estudo mas uma tentativa de estimação probabilística da existência dessas civilizações. Drake não procurava alcançar um número preciso mas sim uma forma de estimular o diálogo científico sobre a busca por inteligência extraterrestre.






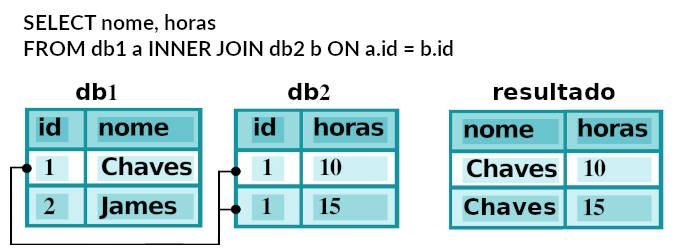
 GROUP BY id
GROUP BY id




 Em um experimento em psicologia social uma pessoa entra em uma sala de espera repleta de pessoas que se levantam toda a vez que soa um alarme. Sem saber que seus companheiros de espera são atores agindo sob combinação prévia com os experimentadores, essa pessoa estranha o fato mas passa a se levantar também. Aos poucos as pessoas vão sendo substituídas até que nenhum dos atores esteja mais na sala. Porém os que restam continuam se levantando, mesmo que, para eles, tal ato não tenha nenhum significado.
Em um experimento em psicologia social uma pessoa entra em uma sala de espera repleta de pessoas que se levantam toda a vez que soa um alarme. Sem saber que seus companheiros de espera são atores agindo sob combinação prévia com os experimentadores, essa pessoa estranha o fato mas passa a se levantar também. Aos poucos as pessoas vão sendo substituídas até que nenhum dos atores esteja mais na sala. Porém os que restam continuam se levantando, mesmo que, para eles, tal ato não tenha nenhum significado. rita pela ciência que justifique o efeito da posição de planetas na formação e condução em vida de um ser humano. Nenhuma das proposições apresentadas pelos praticantes para justificar o mecanismo de funcionamento da astrologia pode ser testada ou refutada.
rita pela ciência que justifique o efeito da posição de planetas na formação e condução em vida de um ser humano. Nenhuma das proposições apresentadas pelos praticantes para justificar o mecanismo de funcionamento da astrologia pode ser testada ou refutada.



 Vivemos em uma cultura que valoriza, por princípio, a fé das pessoas. Em certo sentido a fé pode ser vista como algo construtivo e bom, como a esperança de que poderemos superar os problemas atuais, individuais ou do grupo, e construir tempos melhores. Mas é praxe chamar de fé a confiança em coisas que não podem ser provadas ou verificadas. Não é necessário perguntar se alguém tem fé nas leis de Newton ou na Teoria da Relatividade de Einstein pois elas podem ser verificadas. Ou você conhece essas teorias ou as ignora. Fé é a confiança implícita, muitas vezes inconsciente, em instruções não processadas pelo senso crítico.
Vivemos em uma cultura que valoriza, por princípio, a fé das pessoas. Em certo sentido a fé pode ser vista como algo construtivo e bom, como a esperança de que poderemos superar os problemas atuais, individuais ou do grupo, e construir tempos melhores. Mas é praxe chamar de fé a confiança em coisas que não podem ser provadas ou verificadas. Não é necessário perguntar se alguém tem fé nas leis de Newton ou na Teoria da Relatividade de Einstein pois elas podem ser verificadas. Ou você conhece essas teorias ou as ignora. Fé é a confiança implícita, muitas vezes inconsciente, em instruções não processadas pelo senso crítico.




 Suponha que você acredita na existência de um fenômeno paranormal de qualquer natureza. Não é o objetivo dessa argumentação mostrar que você está errada(o), e muito menos propor outra visão mais “correta ou verdadeira”. Principalmente quando o debate envolve tema de foro muito íntimo, como a existência de (digamos) uma alma imortal, que existe independente do corpo, não deveria haver uma pessoa (ou várias) capazes de confirmar ou desmentir a sua visão. Então, neste caso, ceticismo significa que você deve analisar sua percepção das coisas e descobrir se você sabe algo a respeito ou apenas acredita. Ceticismo consiste em entender que suas crenças tem uma importância relativa e devem ser mantidas sob permanente escrutínio. E, caso você decida que sabe algo (novamente, digamos) sobre a existência da alma, e pode mostrar isso, então você tem um compromisso com a humanidade inteira, demonstrando do modo inequívoco a existência dessa entidade (a alma).
Suponha que você acredita na existência de um fenômeno paranormal de qualquer natureza. Não é o objetivo dessa argumentação mostrar que você está errada(o), e muito menos propor outra visão mais “correta ou verdadeira”. Principalmente quando o debate envolve tema de foro muito íntimo, como a existência de (digamos) uma alma imortal, que existe independente do corpo, não deveria haver uma pessoa (ou várias) capazes de confirmar ou desmentir a sua visão. Então, neste caso, ceticismo significa que você deve analisar sua percepção das coisas e descobrir se você sabe algo a respeito ou apenas acredita. Ceticismo consiste em entender que suas crenças tem uma importância relativa e devem ser mantidas sob permanente escrutínio. E, caso você decida que sabe algo (novamente, digamos) sobre a existência da alma, e pode mostrar isso, então você tem um compromisso com a humanidade inteira, demonstrando do modo inequívoco a existência dessa entidade (a alma).


 Mas, mesmo reconhecendo que nossos mecanismos de contato com o mundo foram finamente ajustados para a sobrevivência, temos muitas indicações de que nossos instrumentos sensoriais não são perfeitos para nos informar sobre o que existe no mundo. Eles podem falhar de maneiras e níveis diversos e nos iludir em várias situações. Por isso uma análise dessas falhas devem ser parte importante de qualquer tentativa de compreender, com algum grau de objetividade, o que está em nosso ambiente.
Mas, mesmo reconhecendo que nossos mecanismos de contato com o mundo foram finamente ajustados para a sobrevivência, temos muitas indicações de que nossos instrumentos sensoriais não são perfeitos para nos informar sobre o que existe no mundo. Eles podem falhar de maneiras e níveis diversos e nos iludir em várias situações. Por isso uma análise dessas falhas devem ser parte importante de qualquer tentativa de compreender, com algum grau de objetividade, o que está em nosso ambiente.
 Parte dessa ilusão se deve à lentidão de nossos sentido e da forma como eles devem se focar sobre o objeto considerado, desprezando a visão ampla do examinado. Quando assistimos a um filme, por exemplo, estamos expostos a uma sequência de imagens estáticas mas as interpretamos como estando em movimento contínuo. Um ponto de luz em rápido movimento circular (como uma brasa amarrada na ponta de uma corda sendo girada) se parece com uma circunferência pois pontos acessos na retina demoram a se apagar de forma que vemos um círculo inteiro quando apenas um ponto está iluminado.
Parte dessa ilusão se deve à lentidão de nossos sentido e da forma como eles devem se focar sobre o objeto considerado, desprezando a visão ampla do examinado. Quando assistimos a um filme, por exemplo, estamos expostos a uma sequência de imagens estáticas mas as interpretamos como estando em movimento contínuo. Um ponto de luz em rápido movimento circular (como uma brasa amarrada na ponta de uma corda sendo girada) se parece com uma circunferência pois pontos acessos na retina demoram a se apagar de forma que vemos um círculo inteiro quando apenas um ponto está iluminado.




 Além da faixa restrita de frequências de ondas que podemos captar, nossa visão só é nítida em uma região muito pequena do campo visual, e desfocada no entorno. Se você esticar o braço e levantar o polegar o tamanho da unha em seu polegar é aproximadamente o mesmo da região onde você enxerga claramente. A imagem periférica é borrada e imprecisa e a noção de que estamos olhando uma imagem ampla e detalhada é construída. (Experimente fixar os olhos em uma parte desse texto e ler as palavras que estão fora de seu olhar direto!) Quando você muda o foco de visão o ponto que recebe sua atenção se ilumina e se torna mais definido enquanto as demais partes da imagem são alimentados pelo cérebro usando a memória e cálculo.
Além da faixa restrita de frequências de ondas que podemos captar, nossa visão só é nítida em uma região muito pequena do campo visual, e desfocada no entorno. Se você esticar o braço e levantar o polegar o tamanho da unha em seu polegar é aproximadamente o mesmo da região onde você enxerga claramente. A imagem periférica é borrada e imprecisa e a noção de que estamos olhando uma imagem ampla e detalhada é construída. (Experimente fixar os olhos em uma parte desse texto e ler as palavras que estão fora de seu olhar direto!) Quando você muda o foco de visão o ponto que recebe sua atenção se ilumina e se torna mais definido enquanto as demais partes da imagem são alimentados pelo cérebro usando a memória e cálculo.
 A percepção do tempo não é linear e pode ser manipulada em experimentos. Qualquer coisa que aconteça e receba toda a nossa atenção parece fluir mais lentamente. Há um experimento que exibe para os sujeitos de teste uma série de imagens contendo discos de cores diferentes, a maioria deles com o mesmo tamanho na tela. Todas as imagens ficam visíveis pelo mesmo tempo. Quando os discos aumentam de tamanho os observadores têm a impressão de que eles ficam visíveis por tempo maior. Uma sugestão para entender isso é a de que os discos que crescem parecem se aproximar do observador e que, evolutivamente, objetos que se aproximam merecem atenção mais detalhada.
A percepção do tempo não é linear e pode ser manipulada em experimentos. Qualquer coisa que aconteça e receba toda a nossa atenção parece fluir mais lentamente. Há um experimento que exibe para os sujeitos de teste uma série de imagens contendo discos de cores diferentes, a maioria deles com o mesmo tamanho na tela. Todas as imagens ficam visíveis pelo mesmo tempo. Quando os discos aumentam de tamanho os observadores têm a impressão de que eles ficam visíveis por tempo maior. Uma sugestão para entender isso é a de que os discos que crescem parecem se aproximar do observador e que, evolutivamente, objetos que se aproximam merecem atenção mais detalhada. Da mesma forma chamamos cobra de cobra, mas isso nem de longe carrega todo o conteúdo que o animal, em si, possui. A palavra cobra não contém, por exemplo, a sequência de DNA necessária para formar o animal. Ela também não carrega o perigo e o medo que sentimos ao avistar uma verdadeira serpente.
Da mesma forma chamamos cobra de cobra, mas isso nem de longe carrega todo o conteúdo que o animal, em si, possui. A palavra cobra não contém, por exemplo, a sequência de DNA necessária para formar o animal. Ela também não carrega o perigo e o medo que sentimos ao avistar uma verdadeira serpente. 

 Na abertura da Copa do Mundo de futebol em 2014 um homem paraplégico se levantou e deu o primeiro chute na bola usando um exoesqueleto controlado por seu cérebro, como parte do Walk Again Project, um esforço colaborativo de 150 pesquisadores coordenados por Nicolelis.
Na abertura da Copa do Mundo de futebol em 2014 um homem paraplégico se levantou e deu o primeiro chute na bola usando um exoesqueleto controlado por seu cérebro, como parte do Walk Again Project, um esforço colaborativo de 150 pesquisadores coordenados por Nicolelis. A memória pessoal não é um fenômeno único mas sim um aglomerado de efeitos. Existe a memória de curta duração que mantemos ativa por alguns segundos, como a que usamos quando lemos um número de telefone em um anúncio e o discamos imediatamente. Também temos memória de longo prazo que são divididas em duas categorias: memória declarativa ou explícita e memória não declarativa ou implícita. Memórias não declarativas são responsáveis por hábitos e habilidades adquiridas, tais como saber manusear talheres, nadar ou andar de bicicleta. Com o uso essas habilidades se tornam automáticas e pode ser usadas com muito pouco esforço. A memoria declarativa é responsável pelo armazenamento de eventos que ocorreram em nossas vidas. Elas são também chamadas biográficas ou episódicas, contendo o conteúdo de nossas vivências e praticamente definem quem somos.
A memória pessoal não é um fenômeno único mas sim um aglomerado de efeitos. Existe a memória de curta duração que mantemos ativa por alguns segundos, como a que usamos quando lemos um número de telefone em um anúncio e o discamos imediatamente. Também temos memória de longo prazo que são divididas em duas categorias: memória declarativa ou explícita e memória não declarativa ou implícita. Memórias não declarativas são responsáveis por hábitos e habilidades adquiridas, tais como saber manusear talheres, nadar ou andar de bicicleta. Com o uso essas habilidades se tornam automáticas e pode ser usadas com muito pouco esforço. A memoria declarativa é responsável pelo armazenamento de eventos que ocorreram em nossas vidas. Elas são também chamadas biográficas ou episódicas, contendo o conteúdo de nossas vivências e praticamente definem quem somos. Os exemplos mostram que uma memória pode ser plantada com alguma antecedência ou até mesmo na hora em que se faz a pergunta. Além disso é possível termos falsas memórias, quando partes de uma memória verdadeira se conectam incorretamente, levantando um quadro falso do que aconteceu. É esse o caso quando você julga que foi o protagonista de uma evento que, na verdade, foi relatado por uma terceira pessoa.
Os exemplos mostram que uma memória pode ser plantada com alguma antecedência ou até mesmo na hora em que se faz a pergunta. Além disso é possível termos falsas memórias, quando partes de uma memória verdadeira se conectam incorretamente, levantando um quadro falso do que aconteceu. É esse o caso quando você julga que foi o protagonista de uma evento que, na verdade, foi relatado por uma terceira pessoa.


 O mecanismo tem uma influência forte em nossa vida social. O debate sobre a liberação de armas para a população, versus uma legislação que restringe a posse de armas, se tornou politicamente envolvente, dificultando muito o atingimento de posições racionais e desapaixonadas. Um defensor do desarmamento tende a buscar, ou a prestar mais atenção, nos casos em que a posse de armas resultou em tragédias e mortes. Alguém do lado oposto coleciona informações sobre eventos onde as armas foram úteis e salvaram vidas.
O mecanismo tem uma influência forte em nossa vida social. O debate sobre a liberação de armas para a população, versus uma legislação que restringe a posse de armas, se tornou politicamente envolvente, dificultando muito o atingimento de posições racionais e desapaixonadas. Um defensor do desarmamento tende a buscar, ou a prestar mais atenção, nos casos em que a posse de armas resultou em tragédias e mortes. Alguém do lado oposto coleciona informações sobre eventos onde as armas foram úteis e salvaram vidas.


 Em 1999 os psicólogos David Dunning e Justin Kruger identificaram o efeito, inicialmente através da consideração do caso de um assaltante de bancos que praticava assaltos com o rosto coberto por suco de limão, na expectativa de estar invisível para as câmeras de segurança. Sua crença se originou do uso de suco de limão como “tinta invisível”. Outros testes confirmaram a existência do efeito, inclusive por meio de experimentos onde pessoas eram treinadas para resolver problemas de lógica. Quanto mais treinadas melhor as pessoas conseguiam avaliar sua competência na solução dos desafios.
Em 1999 os psicólogos David Dunning e Justin Kruger identificaram o efeito, inicialmente através da consideração do caso de um assaltante de bancos que praticava assaltos com o rosto coberto por suco de limão, na expectativa de estar invisível para as câmeras de segurança. Sua crença se originou do uso de suco de limão como “tinta invisível”. Outros testes confirmaram a existência do efeito, inclusive por meio de experimentos onde pessoas eram treinadas para resolver problemas de lógica. Quanto mais treinadas melhor as pessoas conseguiam avaliar sua competência na solução dos desafios. O efeito não ocorre apenas em indivíduos com pouca formação, ignorantes no geral ou ingênuas, nem exclusivamente sobre temas técnicos-científicos. A maioria das pessoas possui pontos fracos em sua formação, à respeito de algum assunto. Por mais especializadas que elas possam ser em temas de seu domínio elas poderão exibir esse defeito de cognição. Uma forma relativamente simples de perceber o viés em grupos consiste em reunir pessoas de uma mesma comunidade, com uma base cultural comum e perguntá-los como se qualificam em relação a tópicos de interesse comum. A absoluta maioria delas se classifica como entre os 10 ou 15% dos melhores motoristas, melhores amigos, pessoas mais honestas, trabalhadores mais eficientes, etc, o que é matematicamente impossível.
O efeito não ocorre apenas em indivíduos com pouca formação, ignorantes no geral ou ingênuas, nem exclusivamente sobre temas técnicos-científicos. A maioria das pessoas possui pontos fracos em sua formação, à respeito de algum assunto. Por mais especializadas que elas possam ser em temas de seu domínio elas poderão exibir esse defeito de cognição. Uma forma relativamente simples de perceber o viés em grupos consiste em reunir pessoas de uma mesma comunidade, com uma base cultural comum e perguntá-los como se qualificam em relação a tópicos de interesse comum. A absoluta maioria delas se classifica como entre os 10 ou 15% dos melhores motoristas, melhores amigos, pessoas mais honestas, trabalhadores mais eficientes, etc, o que é matematicamente impossível. Na atualidade enfrentamos um desafio social gigantesco (e global) que consiste na radicalização de posições estimuladas pelas mídias sociais. As notícias hoje são dirigidas para o perfil esperado do consumidor da informação. Seu perfil é analisado pelos algoritmos de inteligência artificial e tudo o que você recebe está filtrado pelo que você (e seus amigos, em certa medida) escolheram ver anteriormente. Uma pessoa que gosta de armas verá notícias e propagandas sobre armas e será dirigido para o encontro com outros apreciadores de armas. Sua preferência por um político ou ideologia social será explorada ao máximo, até você achar que a maioria das pessoas concordam com você. Nesse sentido estamos todos sob um processo de manipulação muito mais poderoso do que já estivemos, em qualquer tempo passado.
Na atualidade enfrentamos um desafio social gigantesco (e global) que consiste na radicalização de posições estimuladas pelas mídias sociais. As notícias hoje são dirigidas para o perfil esperado do consumidor da informação. Seu perfil é analisado pelos algoritmos de inteligência artificial e tudo o que você recebe está filtrado pelo que você (e seus amigos, em certa medida) escolheram ver anteriormente. Uma pessoa que gosta de armas verá notícias e propagandas sobre armas e será dirigido para o encontro com outros apreciadores de armas. Sua preferência por um político ou ideologia social será explorada ao máximo, até você achar que a maioria das pessoas concordam com você. Nesse sentido estamos todos sob um processo de manipulação muito mais poderoso do que já estivemos, em qualquer tempo passado.





 Você já se perguntou a razão de as lojas colocarem preços fracionários em seus produtos. Que diferença faz um item de mercado a R$39,99 ou R$40,00? Em compras desse tipo quantas vezes você recebeu 1 centavo de troco? Ocorre que temos uma tendência de nos balizar pela análise do primeiro dígito à esquerda. Esse atalho, que economiza o cérebro de um processamento mais dispendioso, pode ser útil algumas vezes mas gera essa prática exploratória comum do consumidor, simples, ingênua mas efetiva, em alguns casos.
Você já se perguntou a razão de as lojas colocarem preços fracionários em seus produtos. Que diferença faz um item de mercado a R$39,99 ou R$40,00? Em compras desse tipo quantas vezes você recebeu 1 centavo de troco? Ocorre que temos uma tendência de nos balizar pela análise do primeiro dígito à esquerda. Esse atalho, que economiza o cérebro de um processamento mais dispendioso, pode ser útil algumas vezes mas gera essa prática exploratória comum do consumidor, simples, ingênua mas efetiva, em alguns casos.
 Há uma história clássica sobre esse efeito: você está na fila de um banco quando três pessoas encapuçadas entram, ordenam que todos deitem no chão e assaltam os caixas, fugindo em seguida. Após o evento todos, naturalmente nervosos, conversam entre si. E dizem: “você viu que tinha um homem barbudo, dando proteção aos assaltantes”. “Havia duas mulheres”. “Algumas pessoas na fila eram cúmplices”. Etc. Quando a polícia chega ouve relatos incongruentes, alguns contando com a presença de 20 ladrões fortemente armados e mal encarados…
Há uma história clássica sobre esse efeito: você está na fila de um banco quando três pessoas encapuçadas entram, ordenam que todos deitem no chão e assaltam os caixas, fugindo em seguida. Após o evento todos, naturalmente nervosos, conversam entre si. E dizem: “você viu que tinha um homem barbudo, dando proteção aos assaltantes”. “Havia duas mulheres”. “Algumas pessoas na fila eram cúmplices”. Etc. Quando a polícia chega ouve relatos incongruentes, alguns contando com a presença de 20 ladrões fortemente armados e mal encarados…





 Você participa de um experimento que sorteia 5 bolas pretas ou vermelhas, com igual probabilidade. Denotando preto por
Você participa de um experimento que sorteia 5 bolas pretas ou vermelhas, com igual probabilidade. Denotando preto por  William Poundstone, escritor de divulgação científica em seu livro Rock Breaks Scissors, explora algumas das ramificações das descobertas de Goodfellow: “Ele basicamente mostrou que muitas das nossas pequenas decisões cotidianas são incrivelmente previsíveis”. Com alguns dados e conhecimento é possível prever muitas atitudes e decisões das pessoas. Por exemplo, no jogo
William Poundstone, escritor de divulgação científica em seu livro Rock Breaks Scissors, explora algumas das ramificações das descobertas de Goodfellow: “Ele basicamente mostrou que muitas das nossas pequenas decisões cotidianas são incrivelmente previsíveis”. Com alguns dados e conhecimento é possível prever muitas atitudes e decisões das pessoas. Por exemplo, no jogo 







