Variáveis Complexas

Nestas notas apresentamos o estudo das variáveis complexas e algumas aplicações, incluindo alguns exercícios resolvidos e exercícios propostos. O resumo não é completo mas procura esclarecer apenas os aspectos da mais importantes da teoria. A leitura dos exercícios resolvidos e a solução dos exercícios propostos é essencial para a plena compreensão do assunto.

Números complexos, variáveis complexas e funções destas variáveis formam um parte da matemática extremamente importante devido à grande quantidade de suas aplicações e porque lançam um entendimento fundamental sobre a base da matemática e sobre o cálculo.

História das Variáveis Complexas

As equações do segundo grau apareceram na Matemática aproximadamente 1700 anos antes de Cristo e se encontram registradas nas tabuletas de argila da Suméria. Em alguns casos elas levavam a raízes de números negativos que, em geral, eram descartadas. O primeiro exemplo de raiz de número negativo foi encontrado em um texto atribuído a Heron de Alexandria, aproximadamente 75 d.C., em um cálculo sobre o desenho de uma pirâmide onde surge a necessidade de se calcular a raiz $\sqrt{84-100}$. Heron, no entanto, simplesmente substituiu este número por $\sqrt{100-84}$.

Em torno do ano de 275 d.C. Diofanto de Alexandria, resolvendo um problema geométrico, chegou à equação do segundo grau
$$
24x^2-172x+366=0
$$
cujas raízes são $x=(\pm 43\sqrt{-167})/12$. Diofanto, no entanto, prosseguiu sem dar maiores explicações sobre o significado da raiz de um número negativo. Por volta de 850 d.C. o matemático indiano Mahavira afirmou que … como na natureza das coisas um negativo não é um quadrado ele não tem, portanto, raiz quadrada. Deve-se a Bhaskara, que viveu aproximadamente de 1114 até 1185, a afirmação: O quadrado de um afirmativo é um afirmativo; e a raiz quadrada de um afirmativo é dupla: positiva e negativa. Não há raiz quadrada de um negativo pois ele não é um quadrado.

Um grande impulso para a descoberta e aprimoramento dos números complexos se deu no início do século XVI quando os algebristas italianos reconheceram a necessidade da adoção de raízes imaginárias, na época também chamadas de raízes impossíveis, para a solução de equações do terceiro grau dos seguintes tipos:
$$
x^{3}+ax=b,\;\; x^{3}=ax+b \;\;\text{ e }\;\; x^{3}+b=ax.
$$
Também as equações do segundo grau apresentavam desafios. Luca Paccioli (1445 – 1514) observou em uma publicação datada de 1494 que a equação $x^2+c=bx$ é solúvel se $b^2 \geq 4c$ enquanto o francês Nicola Chuquet (1445 – 1500) fez observações semelhantes sobre soluções impossíveis em uma publicação de 1484.

Em 1545 Gerônimo Cardano publicou uma fórmula para resolver equações do terceiro grau que ficou conhecida como Fórmula de Cardano embora se saiba que foi Tartaglia quem sugeriu a ele a solução para estas equações. Em seu livro Ars Magna Cardano apresentou o que se considera ser a primeira publicação do conceito de número complexo. Cardano fez a seguinte pergunta: Se alguém pede que você divida 10 em duas partes, que multiplicadas resultariam em 30 ou 40, é evidente que este problema não tem solução. Em seguida ele faz um comentário surpreendente: No entanto, resolveremos isto da seguinte maneira, … e prossegue encontrando as raízes $5+\sqrt{-15}$ e $5-\sqrt{-15}$ cuja soma é $10.$ Neste ponto ele afirmou que, … colocando de lado a tortura mental envolvida, multiplicando as duas raízes temos 25 — (–15). Portanto o produto é 40. Apesar das descobertas de Cardano mais de dois séculos se passaram até que os números complexos fossem aceitos como entidades matemáticas legítimas. Durante este intervalo muitos autores se recusaram a usar tais estranhas entidades.

Em 1572 Raphael Bombelli publicou um livro sobre o mesmo tema onde estudava as raízes da equação $x^{3}=15x+4,$ usando a fórmula de Cardano. Ele mostrou que esta equação, além de possuir uma raiz real $x=4,$ também admite uma raiz na forma de
$$
x=\sqrt[3]{2+\sqrt{-121}} + \sqrt[3]{2-\sqrt{-121}}
$$
que ele, assim como fez Cardano, chamou de um sofisma. Acredita-se que esta foi a primeira vez em que surgiu uma equação que admitia como solução um termo envolvendo raízes de números negativos, embora existisse também uma solução real. Motivado por este fato Bombelli procurou compreender melhor o que estava se passando, embora enfrentando grandes dificuldades, em particular devido a não possuir uma notação adequada. A partir do trabalho de Bombelli os números complexos passaram a ser usados como instrumentos auxiliares de cálculo, mesmo que se duvidasse de sua existência.

A primeira tentativa para atribuir um significado concreto aos números complexos por meio de uma interpretação geométrica é devida a John Wallis (1616 – 1703) em um trabalho onde se fazia analogias entre quantidades imaginárias e quantidades negativas, em seu livro De Algebra Tractatus.

Em 1702 Jean Bernoulli afirmou que um número e seu oposto ($a$ e $-a$ ) tem o mesmo logaritmo. Esse fato intrigou os matemáticos do início do século XVIII que não sabiam como atribuir um valor ao logaritmo de um número negativo. Coube a Euler explicar a questão em 1747, em uma carta dirigida a d’Alembert. Foi Euler quem empregou pela primeira vez a notação $i=$ $\sqrt{-1},$ embora o símbolo $\sqrt{-1}$ já tivesse sido usado Albert Girard em 1629.

Como se pronuncia de Moivre?

No século XVII Descartes percebeu a distinção entre raízes reais e imaginárias embora os principais progressos no estabelecimento da disciplina só foram obtidos no século XVIII, através dos trabalhos de Abraham de Moivre e Euler. Em 1707 de Moivre publicou a solução da equação de grau ímpar por um método análogo ao de Cardano. De Moivre publicou a fórmula que leva seu nome,
$$
(\cos \theta +i\text{sen }\theta )^{n}=\cos (n\theta )+i\text{sen }(n\theta ),
$$
em 1722, inicialmente apenas para alguns valores particulares do argumento $\theta$. Em 1748 Euler mostrou que a fórmula está correta para qualquer valor do argumento, permitindo com isto o cálculo de raízes de números complexos. Neste período começou a se consolidar a representação geométrica para os complexos, o que facilitou muito a sua aceitação por parte dos matemáticos da época e fez com que muitos deles se dedicassem a este tema e contribuíssem para este campo da matemática.

No século XVIII, Kuhn e Caspar Wessel apresentaram novos progressos na direção da teoria atualmente conhecida. Os escritos de Wessel foram publicados nos Anais da Academia de Copenhagen de 1799, sendo um texto extremamente claro e completo, mesmo em comparação com as obras modernas. Ele também considerou a esfera e apresentou uma teoria dos quatérnions a partir da qual desenvolveu um tratamento completo da trigonometria esférica. Em seu texto Wessel apresentou a representação geométrica para os complexos que usamos até os dias de hoje. Seu objetivo, além de justificar os complexos, era o de representar direções de forma analítica. Apesar de ter sido bem sucedido na representação geométrica dos complexos, de definir as operações de soma, subtração, multiplicação e divisão deste números, o artigo estava escrito em dinamarquês e não teve ampla divulgação nem se tornou conhecido dos matemáticos da época.

Em 1804 o abade Buée apresentou independentemente o mesmo conceito sugerido por Wallis, de que $\sqrt{-1}$ deveria ser representado em uma reta perpendicular ao eixo real. O artigo de Buée só foi publicado em 1806, no mesmo ano em Argand produziu um panfleto sobre o mesmo assunto. O trabalho de Argand foi reconhecido como o introdutor da representação geométrica e deu origem ao termo hoje usado, plano de Argand, para representar o plano complexo.

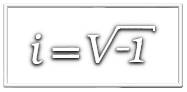
Euler foi o primeiro a usar, em 1777, o símbolo $i$ como a unidade imaginária, $i=\sqrt{-1}.$ Ele observou que $ii=-1$ o que leva à $1/i=-i$. O símbolo, no entanto, só apareceu em uma publicação no ano de 1794 em seu livro Institutionum Calculi Integralis e só foi amplamente divulgado se tornou de uso comum quando Gauss o adotou em 1801. Embora os termos real e imaginário já tivessem sido usados René Descartes em 1637, a expressão número complexo só foi introduzida por Gauss em 1832.

Quando Gauss se interessou pela teoria dos complexos, em 1831, ele a considerou bastante incompleta e trabalhou para aperfeiçoá-la e difundi-la entre os matemáticos da época. Gauss estava interessado em descobrir as propriedades geométricas de quantidades complexas. Assim como Wessel, ele procurava entidades análogas aos complexos que pudessem ser usadas na descrição de direções no espaço tri-dimensional.

A formalização completa dos números complexos como pares ordenados de números reais foi desenvolvida em 1833 por Hamilton e em 1847 por Cauchy. Também se deve mencionar que os esforços de Cauchy e Abel foram importantes para que a teoria fosse amplamente aceita e utilizada. Vários outros matemáticos fizeram contribuições importantes: Kummer (1844), Kronecker (1845), Scheffler (1845, 1851, 1880), Bellavitis (1835, 1852), Peacock (1845), e De Morgan (1849). Também se deve lembrar os artigos de Möbius sobre aplicações geométricas dos complexos, e Dirichlet pela expansão da teoria para envolver os primos, congruências ou reciprocidade, entre outros aspectos estudados.

Além da familiar forma dos complexos, $a+bi$, onde $i$ é a raiz de $x^{2}+1=0,$ outros estudos foram empreendidos. Eisenstein estudou números do tipo de $a+bj$, onde $j$ é a raiz complexa de $x^{3}-1=0$. Uma generalização devida em grande parte a Kummer estuda as raízes complexas derivadas de $x^{k}-1=0,$ onde $k$ é um primo. Galois estudou números complexos baseadas nas raízes imaginárias de uma congruência irredutível $F(x)\equiv 0 (\text{mod }p)$ onde $p$ é primo. Estudos mais recentes da teoria, após o ano de 1884, foram realizados por Weierstrass, Schwarz, Dedekind, Hölder, Berloty, Poincaré, Study e Macfarlane.

A terminologia atualmente empregada na matemática em relação aos complexos é principalmente devida a seus fundadores. Argand chamava $\cos \phi +i\text{sen }\phi $ de fator de direção, e $r=\sqrt{a^{2}+b^{2}}$ o módulo do complexo. Cauchy (1828) denominava $\cos \phi +i\text{sen }\phi $ a forma reduzida l’expression réduite); Gauss usou $i$ para denotar $\sqrt{-1}$, introduziu a expressão número complexo para se referir ao número da forma $a+bi$, com $a$ e $b$ reais, e chamou $a^{2}+b^{2}$ de a norma. A expressão coeficiente de direção, ainda hoje utilizada, é devida a Hankel (1867), e valor absoluto, para módulo, é devida a Weierstrass.

Phylos.net

Pensar e Imaginar

Variáveis Complexas

Variáveis Complexas

História das Variáveis Complexas

Lista de Capítulos

Variáveis Complexas

Leave a Reply Cancel reply