
Para dar um exemplo de análise de fatores usaremos o módulo factor_analyser do Python. Os dados usados são originados do Synthetic Aperture Personality Assessment (SAPA) que contém 25 questões de auto-avaliação pessoais disponíveis na web na página de Vincent Arel-Bundock, no Github.
A documentação do Factor Analyser pode ser lida nessa página.
SAPA e BFI
SAPA, Synthetic Aperture Personality Assessment, é um método usado para avaliar diferenças de personalidade individuais, muito utilizado para pesquisas online. O sujeito testado recebe um subconjunto aleatório dos itens em estudo com o objetivo de reunir grande volume de dados suficientes para a montagem de grandes matrizes de covariância (de relacionamento entre os dados verificados). O teste online foi desenvolvido por William Revelle e é mantido pela Northwestern University, Ilinois, EUA.
A1: Sou indiferente aos sentimentos das outras pessoas.
A2: Sempre pergunto sobre o bem-estar dos outros.
A3: Sei como confortar os outros.
A4: Adoro crianças.
A5: Faço as pessoas se sentirem à vontade.C1: Sou exigente no meu trabalho.
C2: Continuo minhas tarefas até que tudo esteja perfeito.
C3: Faço as coisas de acordo com um plano.
C4: Deixo tarefas semi-acabadas.
C5: Desperdiço meu tempo.E1: Não falo muito.
E2: Tenho dificuldades para abordar outras pessoas.
E3: Sei como cativar as pessoas.
E4: Faço amigos facilmente.
E5: Assumo o controle das situações.
N1: Fico com raiva facilmente.
N2: Irrito-me facilmente.
N3: Tenho alterações de humor frequentes.
N4: Muitas vezes me sinto triste.
N5: Entro em pânico facilmente.
O1: Sempre tenho muitas ideias.
O2: Evito leituras complexas.
O3: Procuro levar as conversas para um nível elevado.
O4: Passo algum tempo refletindo sobre as coisas.
O5: Nunca me detenho a avaliar um assunto profundamente.
A escala usada para respostas usada foi:
1. Totalmente falso
2. Moderadamente falso
3. Um pouco falso
4. Um pouco correto
5. Moderadamente correto
6. Totalmente corretoIndicadores Demográficos:
estão codificados da seguinte forma:
Gênero:
1. Masculino,
2. Feminino.
Idade: a idade (em anos).
Educação:
1. Nível médio incompleto,
2. Nível médio completo,
3. Nível superior incompleto,
4. Nível superior completo,
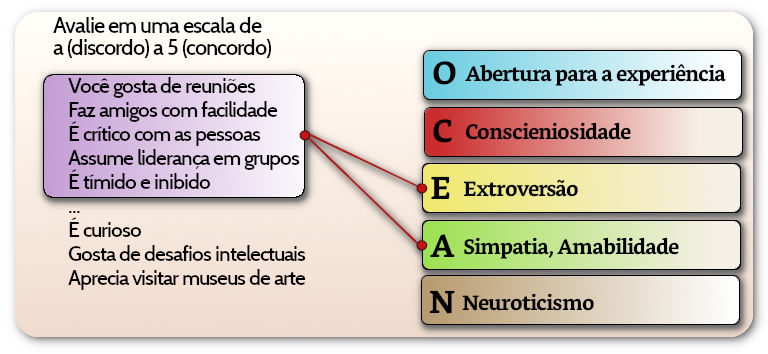
5. Pós-graduação.Fatores esperados:
Os itens estão organizados por fatores esperados (a serem verificados pela análise):
Agreeableness, (Amabilidade),
Conscientiousness, (Conscienciosidade),
Extroversion, (Extroversão),
Neuroticism, (Neuroticismo) e
Opennness, (Abertura).
O arquivo de respostas disponível foi baixado como o nome bfi.csv e salvo na pasta do projeto, subpasta ./dbs. Esse arquivo contém dados no formato *.csv (valores separados por vírgula) relativos a 2800 sujeitos com 3 campos adicionais de dados demográficos: sexo, educação e idade.
Jupyter Notebook e convenções usadas

Jupyter Notebook é uma aplicação web e opensource que permite sessões colaborativas e documentos compartilhados contendo código que pode ser executado dentro da página, equações bem formatadas, visualização gráfica e texto narrativo que podem ser postas sob forma de apresentações ou usadas para desenvolvimento. Seu uso inclui tratamento, transformação e visualização de dados, simulações numéricas, modelagem estatística, machine learning entre outras aplicações.
O projeto será rodado em uma sessão do Jupyter Notebook. Nessa página usamos as seguintes convenções: células de código do Jupyter Notebook aparecem dentro de caixas como a exibida abaixo. Nos notebooks (como no Python) linhas iniciadas pelo sinal “#” são comentários. Apenas nessas páginas outputs simples e compactos podem aparecer como um comentário após o comando como mostrado abaixo (diferente do que ocorre nos notebooks). Outpus mais complexos aparecem em caixas separadas.
# Exemplo de exibição das células do Jupyter Notebook.
print('output simples') # Esse comando imprime 'output simples'
# Outpus mais complexos aparecem em caixas separadas:
print('Outputs do Jupyter Notebook, gráficos e dataframes exibidos aparecem como nesse quadro...')
Módulo Factor Analyser
Factor Analyser é um módulo desenvolvido em Python por Jeremy Biggs e Nitin Madnani, publicado em 2017 para realizar análise fatorial exploratória e confirmatória (AFE, AFC). As classes do pacote são compatíveis com a biblioteca scikit-learn. Partes do código são portadas da biblioteca psych do R.
Tratamento dos dados do bsi por meio do factor_analyser
Instalamos o módulo factor_analyzer dentro do Jupyter Notebook. Em seguida importamos as bibliotecas necessárias: além do próprio factor_analyzer usamos o pandas e numpy para as manipelações de dados e matplotlib para as visualizações.
# Instalação do factor_analyzer:
conda install -c ets factor_analyzer
# Importando bibliotecas (libraries) necessárias
import pandas as pd
import numpy as np
from factor_analyzer import FactorAnalyzer
import matplotlib.pyplot as plt
# A leitura do arquivo de dados para dentro de um dataframe (do pandas)
df = pd.read_csv('./dbs/bfi.csv')
# Renomear a primeira coluna (que está sem nome) para 'id'
df.rename(columns = {'Unnamed: 0':'id'}, inplace = True)
print('A tabela importada contém %d linhas, %d colunas' % df.shape)
print('contendo as seguintes colunas:\n', df.columns)
# Para visualizar a tabela importada:
df.head()
contendo as seguintes colunas:
Index([‘id’, ‘A1’, ‘A2’, ‘A3’, ‘A4’, ‘A5’, ‘C1’, ‘C2’, ‘C3’, ‘C4’, ‘C5’, ‘E1’,
‘E2’, ‘E3’, ‘E4’, ‘E5’, ‘N1’, ‘N2’, ‘N3’, ‘N4’, ‘N5’, ‘O1’, ‘O2’, ‘O3’,
‘O4’, ‘O5’, ‘gender’, ‘education’, ‘age’],
dtype=’object’)
| id | A1 | A2 | A3 | A4 | A5 | C1 | C2 | C3 | C4 | … | N4 | N5 | O1 | O2 | O3 | O4 | O5 | gender | education | age | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 61617 | 2.0 | 4.0 | 3.0 | 4.0 | 4.0 | 2.0 | 3.0 | 3.0 | 4.0 | … | 2.0 | 3.0 | 3.0 | 6 | 3.0 | 4.0 | 3.0 | 1 | NaN | 16 |
| 1 | 61618 | 2.0 | 4.0 | 5.0 | 2.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | … | 5.0 | 5.0 | 4.0 | 2 | 4.0 | 3.0 | 3.0 | 2 | NaN | 18 |
| 2 | 61620 | 5.0 | 4.0 | 5.0 | 4.0 | 4.0 | 4.0 | 5.0 | 4.0 | 2.0 | … | 2.0 | 3.0 | 4.0 | 2 | 5.0 | 5.0 | 2.0 | 2 | NaN | 17 |
| 3 | 61621 | 4.0 | 4.0 | 6.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | 5.0 | … | 4.0 | 1.0 | 3.0 | 3 | 4.0 | 3.0 | 5.0 | 2 | NaN | 17 |
| 4 | 61622 | 2.0 | 3.0 | 3.0 | 4.0 | 5.0 | 4.0 | 4.0 | 5.0 | 3.0 | … | 4.0 | 3.0 | 3.0 | 3 | 4.0 | 3.0 | 3.0 | 1 | NaN | 17 |
2800 rows × 29 columns
Como em qualquer outro uso de dados, principalmente quando importados de fontes externas, fazemos uma verificação de estrutura e completeza ou a existência de valores ausentes (NaN). Os dados demográficos são armazendos em outro dataframe enquanto a avaliação das questões em si são deixadas no dataframe df depois de eliminados os campos relativos a dados demográficos.
# Tabela dfDemografico armazena id, sexo, educação e idade dfDemografico = df[['id', 'gender', 'education', 'age']] # Colunas desnecessárias são eliminadas de df df.drop(['id', 'gender', 'education', 'age'],axis=1,inplace=True) # Possíveis dados ausentes são eliminados df.dropna(inplace=True) # Para verificar as colunas de df df.head(2)
| A1 | A2 | A3 | A4 | A5 | C1 | C2 | C3 | C4 | C5 | … | N1 | N2 | N3 | N4 | N5 | O1 | O2 | O3 | O4 | O5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2.0 | 4.0 | 3.0 | 4.0 | 4.0 | 2.0 | 3.0 | 3.0 | 4.0 | 4.0 | … | 3.0 | 4.0 | 2.0 | 2.0 | 3.0 | 3.0 | 6 | 3.0 | 4.0 | 3.0 |
| 1 | 2.0 | 4.0 | 5.0 | 2.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | 4.0 | … | 3.0 | 3.0 | 3.0 | 5.0 | 5.0 | 4.0 | 2 | 4.0 | 3.0 | 3.0 |
2 rows × 25 columns
# Uma visão geral dos dados no dataframe df pode ser vista: df.info()
Int64Index: 2436 entries, 0 to 2799
Data columns (total 25 columns):
# Column Non-Null Count Dtype
—————————————————————————————
0 A1 2436 non-null float64
1 A2 2436 non-null float64
2 A3 2436 non-null float64
3 A4 2436 non-null float64
4 A5 2436 non-null float64
… Grupos C, E, N omitidos
20 O1 2436 non-null float64
21 O2 2436 non-null int64
22 O3 2436 non-null float64
23 O4 2436 non-null float64
24 O5 2436 non-null float64
dtypes: float64(24), int64(1)
memory usage: 494.8 KB
Observamos que apenas o campo O2 tem tipo de variável int64. Apenas para ter todos os campos do mesmo tipo fazemos a conversão para float64.
# Converter o campo O2 em float df['O2'] = df['O2'].astype(np.float64) type(df['O2'][0]) # Agora o campo é do tipo numpy.float64
Considerando que em operações que faremos podemos perder o nome das colunas, vamos armazenar esses nomes em uma varável (que nesse caso é uma série).
itens=df.columns print(itens)
‘E3’, ‘E4’, ‘E5’, ‘N1’, ‘N2’, ‘N3’, ‘N4’, ‘N5’, ‘O1’, ‘O2’, ‘O3’, ‘O4’,
‘O5′],
dtype=’object’)
Matriz de Correlação

Estamos prontos para encontrar a matriz de correlação entre as variáveis. Cada célula dessa matriz mostra a correlação entre duas variáveis, listadas como labels das linhas e colunas. Por isso ele tem os valores da diagonal iguais a 1 (que é a correlação da variável consigo mesma). A matriz de correlação fornece uma visão geral de interrelacionamento dos dados e é usada como input para análises mais advançadas.
A correlação .corr é um método de dataframes do pandas. Por default o método corr usa os coeficientes de Pearson mas também pode usar os coeficientes Tau de Kendall ou coefficientes de Spearman.
# A matriz de correlação entre todas as respostas na tabela corrMatriz = df.corr() # Para ver apenas as correlações entre variáveis do grupo A corrMatriz[["A1", "A2","A3", "A4","A5"]].head(5)
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| A1 | 1.000000 | -0.350905 | -0.273636 | -0.156754 | -0.192698 |
| A2 | -0.350905 | 1.000000 | 0.503041 | 0.350856 | 0.397400 |
| A3 | -0.273636 | 0.503041 | 1.000000 | 0.384918 | 0.515679 |
| A4 | -0.156754 | 0.350856 | 0.384918 | 1.000000 | 0.325644 |
| A5 | -0.192698 | 0.397400 | 0.515679 | 0.325644 | 1.000000 |
Em seguida fazemos o gráfico de calor (heatmap) da matriz de correlação. Usamos a biblioteca seaborn para isso. Um heatmap associa uma cor a cada valor na matriz de correção. Tons mais escuros de azul (nesse caso) são valores mais perto de 1, tons mais claros são valores mais perto de -1.
import seaborn as sns
plt.figure(figsize=(12,12))
sns.set(font_scale=1)
sns.heatmap(corrMatriz, linewidths=.1, linecolor='#ffffff',
cmap='YlGnBu', xticklabels=1, yticklabels=1)
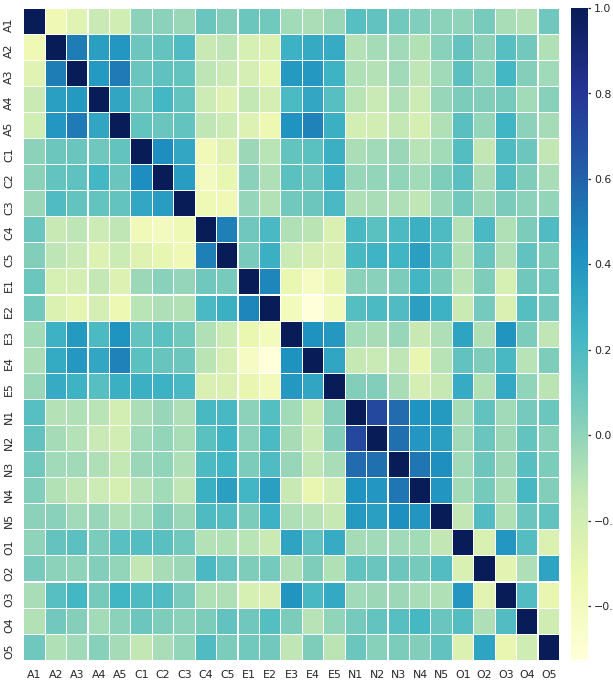

A mera análise do gráfico de calor permite que algumas características da pesquisa sejam visualmente reconhecidas. Duas variáveis diferentes com índice de correlação muito alto podem ser, na verdade, a mesma variável escrita de forma diversa. Nesse caso o pesquisador pode preferir retirar uma delas. Uma ou mais variáveis com nível de correlação muito baixo com todas as demais podem indicar a medida de elementos isolados e fora de contexto com o modelo explorado. Nesse caso vemos agrupamentos claros entre as variáveis A2, A3, A4, A5 e todas as do grupo N, só para citar alguns exemplos.
Análise Fatorial
Análise Fatorial Exploratória, AFE
Podemos agora dar início ao uso específico da Análise Fatorial, começando pela Análise Fatorial Exploratória, AFE, usando o módulo factor_analyzer. O primeiro passo para isso é a avaliação da fatorabilidade dos dados. Isso significa que os dados coletados podem ser agrupados em fatores, que são as nossas variáveis ocultas com o poder de sintetizar e melhor descrever o objeto estudado. Para isso o módulo factor_analyzer oferece dois testes: o Teste de Bartlett e o Teste de Kaiser-Meyer-Olkin.
Teste da esfericidade de Bartlett
O Teste da esfericidade de Bartlett verifica se as variáveis estão correlacionadas entre si, comparando a matriz de correlação com a matriz identidade (que representaria variáveis completamente não correlacionadas).
# Importa o módulo que realiza o teste de Bartlett
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
chi_square_value, p_value = calculate_bartlett_sphericity(df)
print('Teste da Esfericidade de Bartlett: chi² = %d, p_value = %d' % (chi_square_value, p_value))
No nosso caso o teste de Bartlett resulta em p-value = 0, o que indica que os dados podem ser fatorados e a matriz de correlação observada não é a identidade.
Teste de Kaiser-Meyer-Olkin
O Teste de Kaiser-Meyer-Olkin (KMO) fornece uma técnica de avaliação se os dados colhidos são apropriados para esta análise fatorial. Ele realiza um teste para cada variável observada e para o conjunto completo de variáveis. O resultado representa o grau em que cada variável observada pode ser predita, sem erros, pelas demais variáveis no conjunto de dados. KMO é uma estimativa da proporção de variância entre todas as variáveis. Os valores de KMO podem estar entre 0 e 1 e valores abaixo de 0.6 são consideredos inadequados.
# Importa calculate_kmo
from factor_analyzer.factor_analyzer import calculate_kmo
kmo_all,kmo_model = calculate_kmo(df)
print('Valores de kmo_all =\n', kmo_all, '\n')
print('KMO =', kmo_model)
[0.75391928 0.8363196 0.87010963 0.87795367 0.90348747 0.84325413
0.79568263 0.85186857 0.82647206 0.86401687 0.83801873 0.88380544
0.89697008 0.87731273 0.89332158 0.77933902 0.78025018 0.86229919
0.88518467 0.86014155 0.85858672 0.78019798 0.84434957 0.77003158
0.76144469]KMO = 0.848539722194922
Todos os valores de kmo_all são superiores a 0,7 e o KMO geral é KMO = 0.8485 o que são considerados valores muito favoráveis para a análise dos fatores.
Prosseguimos criando uma instância do objeto factor_analysis, tentativamente com 5 fatores
# Criamos objeto factor_analysis, sem rotação e usando 5 fatores (tentativamente)
fa = FactorAnalyzer(5, rotation=None)
# Aplicamos o método fit (ajuste) desse objeto no dataframe
fa.fit(df)
# Depois desse ajuste podemos coletar os autovetores e autovalores
ev, v = fa.get_eigenvalues()
print('São ' + str(len(ev)) + ' autovalores:\n', ev)
[5.13431118 2.75188667 2.14270195 1.85232761 1.54816285 1.07358247
0.83953893 0.79920618 0.71898919 0.68808879 0.67637336 0.65179984
0.62325295 0.59656284 0.56309083 0.54330533 0.51451752 0.49450315
0.48263952 0.448921 0.42336611 0.40067145 0.38780448 0.38185679
0.26253902]
Usando os autovalores calculados traçamos um Screeplot que é um gráfico que lista os autovalores em ordem decrescente, usado para determinar o número de fatores a serem retidos em uma análise fatorial exploratória. O teste, introduzido por R.B. Cattell em 1966, sugere manter tantos fatores quantos forem as autovalores anteriores a uma “dobra mais acentuada” ou “cotovelo” no gráfico. Também é sugerido manter o mesmo número de fatores quantos autovalores existirem maiores que 1.
from bokeh.plotting import figure, output_notebook, show
output_notebook()
eixoX = range(1, len(ev)+1) # de 1 0 26
eixoY = ev
p = figure(title="Scree Plot", x_axis_label='n-ésimo autovalor',y_axis_label='autovalor',
x_range=[0,25], y_range=(0, 6), plot_width=600, plot_height=400,
background_fill_color="#c9b2dd")
p.line(eixoX, eixoY, line_width=1, color = 'black')
p.circle(eixoX, eixoY, size=8, fill_color='red', color="black")
show(p)
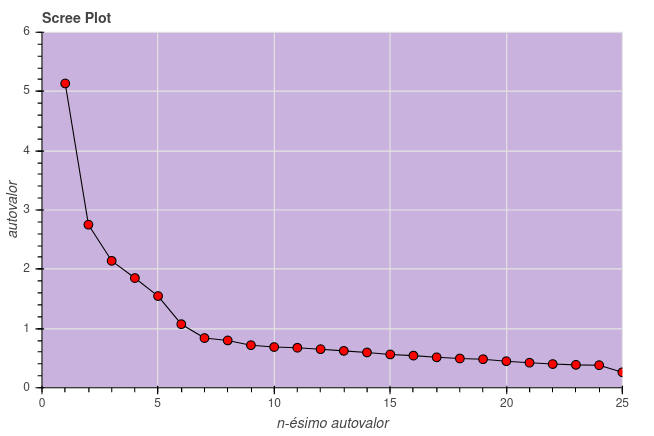
Algumas críticas são dirigidas ao teste feito dessa forma pois ele insere uma decisão pouco objetiva. Mais de um cotovelo podem aparecer no gráfico. De qualquer forma, como veremos no presente caso, o bom senso e a análise posterior dos agrupamentos de fatores podem sugerir uma alteração nesse número.
Cargas Fatoriais (factor loadings)
A carga fatorial é o coeficiente de correlação entre a variável e o fator. Ela mostra a variância explicada pela variável naquele fator em particular.
Prosseguimos criando um objeto FactorAnalyzer com 6 fatores (tentativamente) e usando o método de rotação varimax.
# 6 fatores fa = FactorAnalyzer( 6, rotation="varimax") # o objeto tem o método fit para análise do dataframe fa.fit(df) # Desse extraimos as cargas fatoriais (factor loadings) # Observe que fa.loadings_ é um numpy.array com shape (25,6). Usamos o método # do pandas pd.DataFrame.from_records para convertê-lo em um dataframe factorLoadings = pd.DataFrame.from_records(fa.loadings_) # Para ver a dataframe gerado: factorLoadings.head(4)
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0.095220 | 0.040783 | 0.048734 | -0.530987 | -0.113057 | 0.161216 |
| 1 | 0.033131 | 0.235538 | 0.133714 | 0.661141 | 0.063734 | -0.006244 |
| 2 | -0.009621 | 0.343008 | 0.121353 | 0.605933 | 0.033990 | 0.160106 |
| 3 | -0.081518 | 0.219717 | 0.235140 | 0.404594 | -0.125338 | 0.086356 |
Vemos que os nomes dos itens, de A1 até O5, foram perdidos no cálculo. Vamos renomear tanto esses itens quanto os nomes das colunas (que são os fatores) para ter uma visualização mais clara do que obtivemos até aqui:
# Substitue as linhas pelo nomes dos itens
factorLoadings.index=itens
# Renomeia as colunas
factorLoadings.rename(columns = {0:'Fator 1',
1:'Fator 2',
2:'Fator 3',
3:'Fator 4',
4:'Fator 5',
5:'Fator 6'}, inplace = True)
# Exibe o resultado
factorLoadings
| Fator 1 | Fator 2 | Fator 3 | Fator 4 | Fator 5 | Fator 6 | |
|---|---|---|---|---|---|---|
| A1 | 0.095220 | 0.040783 | 0.048734 | -0.530987 | -0.113057 | 0.161216 |
| A2 | 0.033131 | 0.235538 | 0.133714 | 0.661141 | 0.063734 | -0.006244 |
| A3 | -0.009621 | 0.343008 | 0.121353 | 0.605933 | 0.033990 | 0.160106 |
| A4 | -0.081518 | 0.219717 | 0.235140 | 0.404594 | -0.125338 | 0.086356 |
| A5 | -0.149616 | 0.414458 | 0.106382 | 0.469698 | 0.030977 | 0.236519 |
| C1 | -0.004358 | 0.077248 | 0.554582 | 0.007511 | 0.190124 | 0.095035 |
| C2 | 0.068330 | 0.038370 | 0.674545 | 0.057055 | 0.087593 | 0.152775 |
| C3 | -0.039994 | 0.031867 | 0.551164 | 0.101282 | -0.011338 | 0.008996 |
| C4 | 0.216283 | -0.066241 | -0.638475 | -0.102617 | -0.143846 | 0.318359 |
| C5 | 0.284187 | -0.180812 | -0.544838 | -0.059955 | 0.025837 | 0.132423 |
| E1 | 0.022280 | -0.590451 | 0.053915 | -0.130851 | -0.071205 | 0.156583 |
| E2 | 0.233624 | -0.684578 | -0.088497 | -0.116716 | -0.045561 | 0.115065 |
| E3 | -0.000895 | 0.556774 | 0.103390 | 0.179396 | 0.241180 | 0.267291 |
| E4 | -0.136788 | 0.658395 | 0.113798 | 0.241143 | -0.107808 | 0.158513 |
| E5 | 0.034490 | 0.507535 | 0.309813 | 0.078804 | 0.200821 | 0.008747 |
| N1 | 0.805806 | 0.068011 | -0.051264 | -0.174849 | -0.074977 | -0.096266 |
| N2 | 0.789832 | 0.022958 | -0.037477 | -0.141134 | 0.006726 | -0.139823 |
| N3 | 0.725081 | -0.065687 | -0.059039 | -0.019184 | -0.010664 | 0.062495 |
| N4 | 0.578319 | -0.345072 | -0.162174 | 0.000403 | 0.062916 | 0.147551 |
| N5 | 0.523097 | -0.161675 | -0.025305 | 0.090125 | -0.161892 | 0.120049 |
| O1 | -0.020004 | 0.225339 | 0.133201 | 0.005178 | 0.479477 | 0.218690 |
| O2 | 0.156230 | -0.001982 | -0.086047 | 0.043989 | -0.496640 | 0.134693 |
| O3 | 0.011851 | 0.325954 | 0.093880 | 0.076642 | 0.566128 | 0.210777 |
| O4 | 0.207281 | -0.177746 | -0.005671 | 0.133656 | 0.349227 | 0.178068 |
| O5 | 0.063234 | -0.014221 | -0.047059 | -0.057561 | -0.576743 | 0.135936 |
Vamos montar mais um heatmap com essa tabela.
# A bibioteca seaborn já foi importada como sns plt.figure(figsize=(8,6)) sns.set(font_scale=.9) sns.heatmap(factorLoadings, linewidths=1, linecolor='#ffffff', cmap="YlGnBu", xticklabels=1, yticklabels=1)
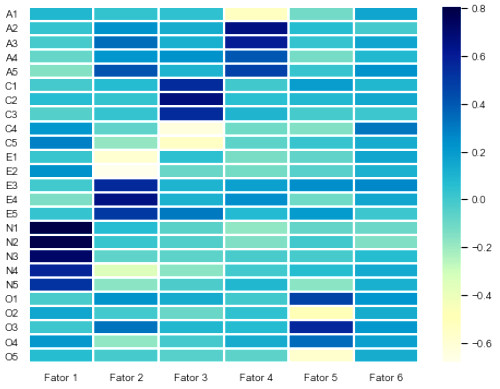
Lembrando que as cores mais escuras indicam correlação direta e as mais claras correlação inversa, percebemos que existem cargas mais fortes entre os itens N1, N2, N3, N4 e N5 com o fator 1, E1 até E5 no fator 2, etc. Nenhum dos itens, no entanto, tem carga relevante no sexto fator. Isso indica que podemos refazer o cálculo de cargas fatoriais com apenas 5 fatores.
# Refazendo o cáculo com 5 fatores apenas
# Apaga a variável fa
del fa
fa = FactorAnalyzer( 5, rotation="varimax")
fa.fit(df)
factorLoadings = pd.DataFrame.from_records(fa.loadings_)
# Renomeia itens
factorLoadings.index=itens
# Renomeia as colunas (fatores)
factorLoadings.rename(columns = {0:'Fator 1',
1:'Fator 2',
2:'Fator 3',
3:'Fator 4',
4:'Fator 5'}, inplace = True)
# Exibe o resultado
factorLoadings
| Fator 1 | Fator 2 | Fator 3 | Fator 4 | Fator 5 | |
|---|---|---|---|---|---|
| A1 | 0.111126 | 0.040465 | 0.022798 | -0.428166 | -0.077931 |
| A2 | 0.029588 | 0.213716 | 0.139037 | 0.626946 | 0.062139 |
| A3 | 0.009357 | 0.317848 | 0.109331 | 0.650743 | 0.056196 |
| A4 | -0.066476 | 0.204566 | 0.230584 | 0.435624 | -0.112700 |
| A5 | -0.122113 | 0.393034 | 0.087869 | 0.537087 | 0.066708 |
| C1 | 0.010416 | 0.070184 | 0.545824 | 0.038878 | 0.209584 |
| C2 | 0.089574 | 0.033270 | 0.648731 | 0.102782 | 0.115434 |
| C3 | -0.030855 | 0.023907 | 0.557036 | 0.111578 | -0.005183 |
| C4 | 0.240410 | -0.064984 | -0.633806 | -0.037498 | -0.107535 |
| C5 | 0.290318 | -0.176395 | -0.562467 | -0.047525 | 0.036822 |
| E1 | 0.042819 | -0.574835 | 0.033144 | -0.104813 | -0.058795 |
| E2 | 0.244743 | -0.678731 | -0.102483 | -0.112517 | -0.042010 |
| E3 | 0.024180 | 0.536816 | 0.083010 | 0.257906 | 0.280877 |
| E4 | -0.115614 | 0.646833 | 0.102023 | 0.306101 | -0.073422 |
| E5 | 0.036145 | 0.504069 | 0.312899 | 0.090354 | 0.213739 |
| N1 | 0.786807 | 0.078923 | -0.045997 | -0.216363 | -0.084704 |
| N2 | 0.754109 | 0.027301 | -0.030568 | -0.193744 | -0.010304 |
| N3 | 0.731721 | -0.061430 | -0.067084 | -0.027712 | -0.004217 |
| N4 | 0.590602 | -0.345388 | -0.178902 | 0.005886 | 0.075225 |
| N5 | 0.537858 | -0.161291 | -0.037309 | 0.100931 | -0.149769 |
| O1 | -0.002224 | 0.213005 | 0.115080 | 0.061550 | 0.504907 |
| O2 | 0.175788 | 0.004560 | -0.099729 | 0.081809 | -0.468925 |
| O3 | 0.026736 | 0.310956 | 0.076873 | 0.126889 | 0.596007 |
| O4 | 0.220582 | -0.191196 | -0.021906 | 0.155475 | 0.369012 |
| O5 | 0.085401 | -0.005347 | -0.062730 | -0.010384 | -0.533778 |
Construimos o heatmap com essa tabela de 5 fatores.
plt.figure(figsize=(8,6)) sns.set(font_scale=.9) sns.heatmap(factorLoadings, linewidths=1, linecolor='#ffffff', cmap="YlGnBu", xticklabels=1, yticklabels=1)
preta indicando grupos
de correlação foram
acrescentados manualmente.

Pelo heatmap percebemos que o grupo de itens N está associado ao fator 1 (Neuroticismo), E ao fator 2 (Extroversão), C ao fator 3 (Conscienciosidade), A ao fator 4 (Amabilidade) e O ao fator 5 (Abertura), previamente identificados. É claro que essa identificação do fator foi realizada pelos pesquisadores no caso dessa pesquisa em particular. Para uma pesquisa nova seria necessário um estudo para o entendimento da natureza de cada fator.
Observe ainda que correlação negativa é correlação. É o que ocorre, por exemplo entre os itens A1 (Sou indiferente aos sentimentos das outras pessoas) e A2 (Sempre pergunto sobre o bem-estar dos outros). A correlação entre eles pode ser obtida da matriz de correlação, corrMatriz['A1']['A2'] = -0.35091.
Observamos que existem as seguintes correspondências entre os grupos de questões e os fatores propostos:
| Fator | Grupo | Descrição |
|---|---|---|
| 1 | N | Neuroticismo |
| 2 | E | Extroversão |
| 3 | C | Conscienciosidade |
| 4 | A | Amabilidade |
| 5 | O | Abertura |
Vamos, portanto, renomear as colunas de nossa matriz de cargas fatoriais para refletir esse entendimento:
# Renomeia as colunas (fatores)
factorLoadings.rename(columns = {'Fator 1':'Neuroticismo',
'Fator 2':'Extroversão',
'Fator 3':'Conscienciosidade',
'Fator 4':'Amabilidade',
'Fator 5':'Abertura'}, inplace = True)
# Exibe o resultado (só duas linhas)
factorLoadings.head(2)
| Neuroticismo | Extroversão | Conscienciosidade | Amabilidade | Abertura | |
|---|---|---|---|---|---|
| A1 | 0.111126 | 0.040465 | 0.022798 | -0.428166 | -0.077931 |
| A2 | 0.029588 | 0.213716 | 0.139037 | 0.626946 | 0.062139 |
Comunalidades
Comunalidades são a soma das cargas fatoriais ao quadrado de cada variável medida. Denotando por \(l_{ij}\) os elementos da matriz da cargas fatoriais a comunalidade da i-ésima variável é \(h_i^2\) dado por
$$
h_i^2 =\Sigma_{j=1}^n l_{ij}^2
$$
Por exemplo, a comunalidade relativa à questão A1 é a soma dos elementos (ao quadrado) da primeira linha da matriz de cargas fatoriais acima:
(0.111126)**2 + (0.040465)**2 + (0.022798)**2 + (-0.428166)**2 +(-0.077931)**2
As comunalidades relativas a todas as variáveis podem ser obtidas com get_communalities() que retorna um numpy.ndarray com dimensões (25,):
fa.get_communalities()
0.34839471, 0.45387181, 0.32428892, 0.47669926, 0.43538283,
0.34780933, 0.545502 , 0.44105495, 0.54125654, 0.40714621,
0.68139838, 0.60800298, 0.54447487, 0.50580328, 0.34931564,
0.31733902, 0.26745151, 0.47464268, 0.2460347 , 0.29628368])
A soma de todos os valores de comunalidade é o valor de comunalidade total:
fa.get_communalities().sum()
Para exibir uma tabela com os nomes da variáveis e suas respectivas comunalidades vamos construir um dataframe contendo esses dados. Lembrando que já temos a variável itens = ['A1', 'A2', ..., 'O4','O5']:
dfComunalidades = pd.DataFrame(comunalidades) dfComunalidades.index = itens
| Variável | Comunalidade |
|---|---|
| A1 | 0.203905 |
| A2 | 0.462803 |
| A3 | 0.539692 |
| A4 | 0.301905 |
| A5 | 0.470020 |
| C1 | 0.348395 |
| C2 | 0.453872 |
| C3 | 0.324289 |
| C4 | 0.476699 |
| C5 | 0.435383 |
| Variável | Comunalidade |
|---|---|
| E1 | 0.347809 |
| E2 | 0.545502 |
| E3 | 0.441055 |
| E4 | 0.541257 |
| E5 | 0.407146 |
| N1 | 0.681398 |
| N2 | 0.608003 |
| N3 | 0.544475 |
| N4 | 0.505803 |
| N5 | 0.349316 |
| Variável | Comunalidade |
|---|---|
| O1 | 0.317339 |
| O2 | 0.267452 |
| O3 | 0.474643 |
| O4 | 0.246035 |
| O5 | 0.296284 |
| Total | 10.5905 |
| Como temos 25 fatores: | |
| Total/25 | 0.4236 |
Podemos pensar na comunalidade de uma variável como a proporção de variação nessa variável explicada pelos fatores propostos no modelo. Por exemplo, a variável N1 tem a maior comunalidade (0.681398) nesse modelo, indicando que aproximadamente 69% da variação nas respostas para “N1: Fico com raiva facilmente” é explicada pelo modelo de 5 fatores proposto enquanto esse valor é de apenas 20% para “A1: Sou indiferente aos sentimentos das outras pessoas”.
Comunalidades servem para avaliar o desempenho do modelo. Valores mais próximos de um indicam que o modelo explica a maior parte da variação para essas variáveis. Nesse caso o modelo está melhor ajustado para as variáveis do grupo N (neuroticismo) e menos eficiente para as variáveis do grupo O (abertura).
A Comunalidade total é de 10.5905 que, dividido entre as 25 variáveis indica uma média de 10.5905/25 = 0.4236 geral para o modelo, ou seja, uma eficiência média de 42% do modelo em explicar a variação de cada variável do teste.
Bibliografia
- Goldberg, L. R.: A broad-bandwidth, public domain, personality inventory measuring the lower-level facets of several five-factor models. In I. Mervielde, I. Deary, F. De Fruyt, & F. Ostendorf (Eds.), Personality Psychology in Europe, Vol. 7 (pp. 7-28). Tilburg, The Netherlands: Tilburg University Press, 1999.
- Biggs, Jeremy: Factor Analyser Documentation, acessado em dezembro de 2020.
- Site Datacamp: Navlani, Avinash: Introduction to Factor Analysis in Python, abril de 2019, acessado em dezembro de 2020.
