
História da Matemática
- Matemática na Grécia Antiga
- Matemática na Idade Moderna
- A História do Cálculo
- História dos Símbolos Matemáticos





Um problema de lógica razoavelmente difícil!

Segue um exemplo de um tipo de questão recorrente em testes de admissão em empresas de tecnologia. Outras soluções, além da aqui apresentada, são encontradas em sites, como por exemplo no canal do Youtube Universo Narrado.
Dois arcos perpendiculares seccionam um círculo, como mostrado na figura 1. Qual é o raio do círculo?

Dados dois pontos A e B que estão do mesmo lado de uma reta r e não são pontos desta reta, qual é o caminho mais curto ligando A e B e que toca a reta r, (figura 3)?
Conta-se que Gauss teria encontrado a soma dos 100 primeiros inteiros em 30 segundos, na escola primária. Seu professor, aborrecido com a algazarra que faziam as crianças, teria mandado que todos calculassem esta soma e Gauss apresentou a resposta rapidamente. Esta é, na verdade, uma operação que pode ser feita de cabeça se você tiver a criatividade de Gauss …

Esta questão apareceu no SAT americano (um teste usado para admissões nas universidades, aplicado no mundo todo) em 1982. Apenas 3 alunos entre os 300 mil que fizeram o teste acertaram. Até os examinadores que prepararam o problema erraram a solução e a questão teve que ser retirada da pontuação. No entanto é possível resolver essa questão com conhecimentos do nosso ensino médio.
O raio do disco A (vermelho, na figura 6) é de 1/3 do raio do disco B (cinza). O disco A desliza sem escorregar sobre o disco B até dar uma volta completa em torno do disco B e retornar para a sua posição original.
Quantas voltas o disco A terá dado em torno de si mesmo?

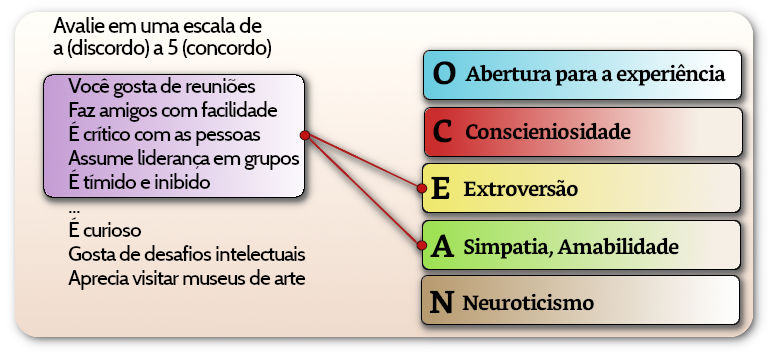
Para dar um exemplo de análise de fatores usaremos o módulo factor_analyser do Python. Os dados usados são originados do Synthetic Aperture Personality Assessment (SAPA) que contém 25 questões de auto-avaliação pessoais disponíveis na web na página de Vincent Arel-Bundock, no Github.
A documentação do Factor Analyser pode ser lida nessa página.
SAPA, Synthetic Aperture Personality Assessment, é um método usado para avaliar diferenças de personalidade individuais, muito utilizado para pesquisas online. O sujeito testado recebe um subconjunto aleatório dos itens em estudo com o objetivo de reunir grande volume de dados suficientes para a montagem de grandes matrizes de covariância (de relacionamento entre os dados verificados). O teste online foi desenvolvido por William Revelle e é mantido pela Northwestern University, Ilinois, EUA.
N1: Fico com raiva facilmente.
N2: Irrito-me facilmente.
N3: Tenho alterações de humor frequentes.
N4: Muitas vezes me sinto triste.
N5: Entro em pânico facilmente.
O1: Sempre tenho muitas ideias.
O2: Evito leituras complexas.
O3: Procuro levar as conversas para um nível elevado.
O4: Passo algum tempo refletindo sobre as coisas.
O5: Nunca me detenho a avaliar um assunto profundamente.
O arquivo de respostas disponível foi baixado como o nome bfi.csv e salvo na pasta do projeto, subpasta ./dbs. Esse arquivo contém dados no formato *.csv (valores separados por vírgula) relativos a 2800 sujeitos com 3 campos adicionais de dados demográficos: sexo, educação e idade.

Jupyter Notebook é uma aplicação web e opensource que permite sessões colaborativas e documentos compartilhados contendo código que pode ser executado dentro da página, equações bem formatadas, visualização gráfica e texto narrativo que podem ser postas sob forma de apresentações ou usadas para desenvolvimento. Seu uso inclui tratamento, transformação e visualização de dados, simulações numéricas, modelagem estatística, machine learning entre outras aplicações.
O projeto será rodado em uma sessão do Jupyter Notebook. Nessa página usamos as seguintes convenções: células de código do Jupyter Notebook aparecem dentro de caixas como a exibida abaixo. Nos notebooks (como no Python) linhas iniciadas pelo sinal “#” são comentários. Apenas nessas páginas outputs simples e compactos podem aparecer como um comentário após o comando como mostrado abaixo (diferente do que ocorre nos notebooks). Outpus mais complexos aparecem em caixas separadas.
# Exemplo de exibição das células do Jupyter Notebook.
print('output simples') # Esse comando imprime 'output simples'
# Outpus mais complexos aparecem em caixas separadas:
print('Outputs do Jupyter Notebook, gráficos e dataframes exibidos aparecem como nesse quadro...')
Factor Analyser é um módulo desenvolvido em Python por Jeremy Biggs e Nitin Madnani, publicado em 2017 para realizar análise fatorial exploratória e confirmatória (AFE, AFC). As classes do pacote são compatíveis com a biblioteca scikit-learn. Partes do código são portadas da biblioteca psych do R.
Instalamos o módulo factor_analyzer dentro do Jupyter Notebook. Em seguida importamos as bibliotecas necessárias: além do próprio factor_analyzer usamos o pandas e numpy para as manipelações de dados e matplotlib para as visualizações.
# Instalação do factor_analyzer:
conda install -c ets factor_analyzer
# Importando bibliotecas (libraries) necessárias
import pandas as pd
import numpy as np
from factor_analyzer import FactorAnalyzer
import matplotlib.pyplot as plt
# A leitura do arquivo de dados para dentro de um dataframe (do pandas)
df = pd.read_csv('./dbs/bfi.csv')
# Renomear a primeira coluna (que está sem nome) para 'id'
df.rename(columns = {'Unnamed: 0':'id'}, inplace = True)
print('A tabela importada contém %d linhas, %d colunas' % df.shape)
print('contendo as seguintes colunas:\n', df.columns)
# Para visualizar a tabela importada:
df.head()
| id | A1 | A2 | A3 | A4 | A5 | C1 | C2 | C3 | C4 | … | N4 | N5 | O1 | O2 | O3 | O4 | O5 | gender | education | age | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 61617 | 2.0 | 4.0 | 3.0 | 4.0 | 4.0 | 2.0 | 3.0 | 3.0 | 4.0 | … | 2.0 | 3.0 | 3.0 | 6 | 3.0 | 4.0 | 3.0 | 1 | NaN | 16 |
| 1 | 61618 | 2.0 | 4.0 | 5.0 | 2.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | … | 5.0 | 5.0 | 4.0 | 2 | 4.0 | 3.0 | 3.0 | 2 | NaN | 18 |
| 2 | 61620 | 5.0 | 4.0 | 5.0 | 4.0 | 4.0 | 4.0 | 5.0 | 4.0 | 2.0 | … | 2.0 | 3.0 | 4.0 | 2 | 5.0 | 5.0 | 2.0 | 2 | NaN | 17 |
| 3 | 61621 | 4.0 | 4.0 | 6.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | 5.0 | … | 4.0 | 1.0 | 3.0 | 3 | 4.0 | 3.0 | 5.0 | 2 | NaN | 17 |
| 4 | 61622 | 2.0 | 3.0 | 3.0 | 4.0 | 5.0 | 4.0 | 4.0 | 5.0 | 3.0 | … | 4.0 | 3.0 | 3.0 | 3 | 4.0 | 3.0 | 3.0 | 1 | NaN | 17 |
2800 rows × 29 columns
Como em qualquer outro uso de dados, principalmente quando importados de fontes externas, fazemos uma verificação de estrutura e completeza ou a existência de valores ausentes (NaN). Os dados demográficos são armazendos em outro dataframe enquanto a avaliação das questões em si são deixadas no dataframe df depois de eliminados os campos relativos a dados demográficos.
# Tabela dfDemografico armazena id, sexo, educação e idade dfDemografico = df[['id', 'gender', 'education', 'age']] # Colunas desnecessárias são eliminadas de df df.drop(['id', 'gender', 'education', 'age'],axis=1,inplace=True) # Possíveis dados ausentes são eliminados df.dropna(inplace=True) # Para verificar as colunas de df df.head(2)
| A1 | A2 | A3 | A4 | A5 | C1 | C2 | C3 | C4 | C5 | … | N1 | N2 | N3 | N4 | N5 | O1 | O2 | O3 | O4 | O5 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 2.0 | 4.0 | 3.0 | 4.0 | 4.0 | 2.0 | 3.0 | 3.0 | 4.0 | 4.0 | … | 3.0 | 4.0 | 2.0 | 2.0 | 3.0 | 3.0 | 6 | 3.0 | 4.0 | 3.0 |
| 1 | 2.0 | 4.0 | 5.0 | 2.0 | 5.0 | 5.0 | 4.0 | 4.0 | 3.0 | 4.0 | … | 3.0 | 3.0 | 3.0 | 5.0 | 5.0 | 4.0 | 2 | 4.0 | 3.0 | 3.0 |
2 rows × 25 columns
# Uma visão geral dos dados no dataframe df pode ser vista: df.info()
Observamos que apenas o campo O2 tem tipo de variável int64. Apenas para ter todos os campos do mesmo tipo fazemos a conversão para float64.
# Converter o campo O2 em float df['O2'] = df['O2'].astype(np.float64) type(df['O2'][0]) # Agora o campo é do tipo numpy.float64
Considerando que em operações que faremos podemos perder o nome das colunas, vamos armazenar esses nomes em uma varável (que nesse caso é uma série).
itens=df.columns print(itens)

Estamos prontos para encontrar a matriz de correlação entre as variáveis. Cada célula dessa matriz mostra a correlação entre duas variáveis, listadas como labels das linhas e colunas. Por isso ele tem os valores da diagonal iguais a 1 (que é a correlação da variável consigo mesma). A matriz de correlação fornece uma visão geral de interrelacionamento dos dados e é usada como input para análises mais advançadas.
A correlação .corr é um método de dataframes do pandas. Por default o método corr usa os coeficientes de Pearson mas também pode usar os coeficientes Tau de Kendall ou coefficientes de Spearman.
# A matriz de correlação entre todas as respostas na tabela corrMatriz = df.corr() # Para ver apenas as correlações entre variáveis do grupo A corrMatriz[["A1", "A2","A3", "A4","A5"]].head(5)
| A1 | A2 | A3 | A4 | A5 | |
|---|---|---|---|---|---|
| A1 | 1.000000 | -0.350905 | -0.273636 | -0.156754 | -0.192698 |
| A2 | -0.350905 | 1.000000 | 0.503041 | 0.350856 | 0.397400 |
| A3 | -0.273636 | 0.503041 | 1.000000 | 0.384918 | 0.515679 |
| A4 | -0.156754 | 0.350856 | 0.384918 | 1.000000 | 0.325644 |
| A5 | -0.192698 | 0.397400 | 0.515679 | 0.325644 | 1.000000 |
Em seguida fazemos o gráfico de calor (heatmap) da matriz de correlação. Usamos a biblioteca seaborn para isso. Um heatmap associa uma cor a cada valor na matriz de correção. Tons mais escuros de azul (nesse caso) são valores mais perto de 1, tons mais claros são valores mais perto de -1.
import seaborn as sns
plt.figure(figsize=(12,12))
sns.set(font_scale=1)
sns.heatmap(corrMatriz, linewidths=.1, linecolor='#ffffff',
cmap='YlGnBu', xticklabels=1, yticklabels=1)
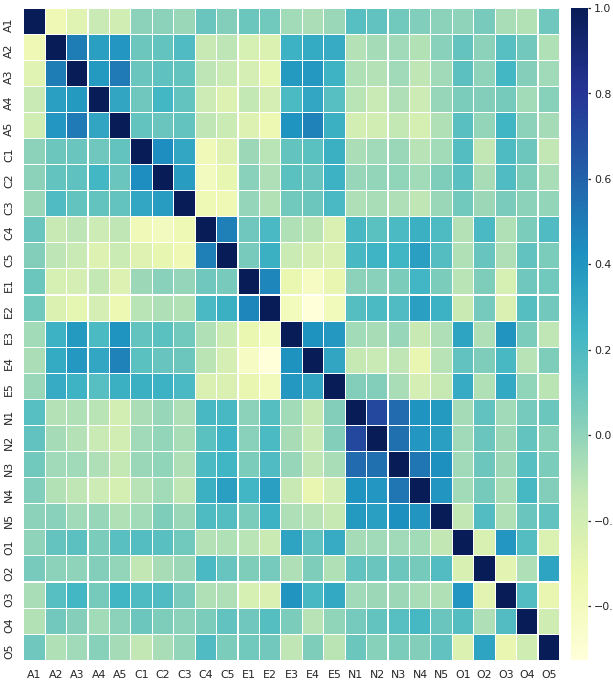

A mera análise do gráfico de calor permite que algumas características da pesquisa sejam visualmente reconhecidas. Duas variáveis diferentes com índice de correlação muito alto podem ser, na verdade, a mesma variável escrita de forma diversa. Nesse caso o pesquisador pode preferir retirar uma delas. Uma ou mais variáveis com nível de correlação muito baixo com todas as demais podem indicar a medida de elementos isolados e fora de contexto com o modelo explorado. Nesse caso vemos agrupamentos claros entre as variáveis A2, A3, A4, A5 e todas as do grupo N, só para citar alguns exemplos.
Podemos agora dar início ao uso específico da Análise Fatorial, começando pela Análise Fatorial Exploratória, AFE, usando o módulo factor_analyzer. O primeiro passo para isso é a avaliação da fatorabilidade dos dados. Isso significa que os dados coletados podem ser agrupados em fatores, que são as nossas variáveis ocultas com o poder de sintetizar e melhor descrever o objeto estudado. Para isso o módulo factor_analyzer oferece dois testes: o Teste de Bartlett e o Teste de Kaiser-Meyer-Olkin.
O Teste da esfericidade de Bartlett verifica se as variáveis estão correlacionadas entre si, comparando a matriz de correlação com a matriz identidade (que representaria variáveis completamente não correlacionadas).
# Importa o módulo que realiza o teste de Bartlett
from factor_analyzer.factor_analyzer import calculate_bartlett_sphericity
chi_square_value, p_value = calculate_bartlett_sphericity(df)
print('Teste da Esfericidade de Bartlett: chi² = %d, p_value = %d' % (chi_square_value, p_value))
No nosso caso o teste de Bartlett resulta em p-value = 0, o que indica que os dados podem ser fatorados e a matriz de correlação observada não é a identidade.
O Teste de Kaiser-Meyer-Olkin (KMO) fornece uma técnica de avaliação se os dados colhidos são apropriados para esta análise fatorial. Ele realiza um teste para cada variável observada e para o conjunto completo de variáveis. O resultado representa o grau em que cada variável observada pode ser predita, sem erros, pelas demais variáveis no conjunto de dados. KMO é uma estimativa da proporção de variância entre todas as variáveis. Os valores de KMO podem estar entre 0 e 1 e valores abaixo de 0.6 são consideredos inadequados.
# Importa calculate_kmo
from factor_analyzer.factor_analyzer import calculate_kmo
kmo_all,kmo_model = calculate_kmo(df)
print('Valores de kmo_all =\n', kmo_all, '\n')
print('KMO =', kmo_model)
Todos os valores de kmo_all são superiores a 0,7 e o KMO geral é KMO = 0.8485 o que são considerados valores muito favoráveis para a análise dos fatores.
Prosseguimos criando uma instância do objeto factor_analysis, tentativamente com 5 fatores
# Criamos objeto factor_analysis, sem rotação e usando 5 fatores (tentativamente)
fa = FactorAnalyzer(5, rotation=None)
# Aplicamos o método fit (ajuste) desse objeto no dataframe
fa.fit(df)
# Depois desse ajuste podemos coletar os autovetores e autovalores
ev, v = fa.get_eigenvalues()
print('São ' + str(len(ev)) + ' autovalores:\n', ev)
Usando os autovalores calculados traçamos um Screeplot que é um gráfico que lista os autovalores em ordem decrescente, usado para determinar o número de fatores a serem retidos em uma análise fatorial exploratória. O teste, introduzido por R.B. Cattell em 1966, sugere manter tantos fatores quantos forem as autovalores anteriores a uma “dobra mais acentuada” ou “cotovelo” no gráfico. Também é sugerido manter o mesmo número de fatores quantos autovalores existirem maiores que 1.
from bokeh.plotting import figure, output_notebook, show
output_notebook()
eixoX = range(1, len(ev)+1) # de 1 0 26
eixoY = ev
p = figure(title="Scree Plot", x_axis_label='n-ésimo autovalor',y_axis_label='autovalor',
x_range=[0,25], y_range=(0, 6), plot_width=600, plot_height=400,
background_fill_color="#c9b2dd")
p.line(eixoX, eixoY, line_width=1, color = 'black')
p.circle(eixoX, eixoY, size=8, fill_color='red', color="black")
show(p)
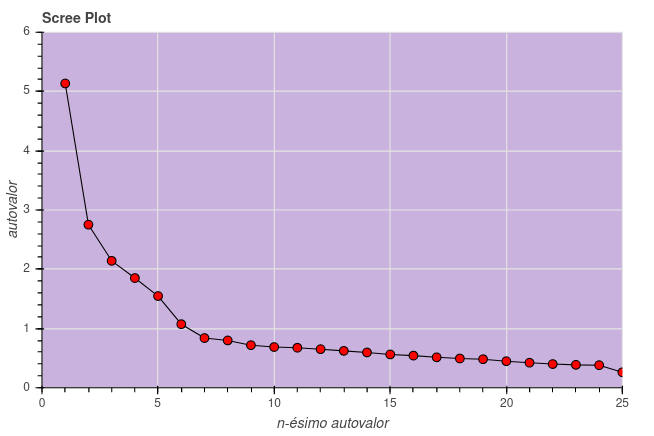
Algumas críticas são dirigidas ao teste feito dessa forma pois ele insere uma decisão pouco objetiva. Mais de um cotovelo podem aparecer no gráfico. De qualquer forma, como veremos no presente caso, o bom senso e a análise posterior dos agrupamentos de fatores podem sugerir uma alteração nesse número.
A carga fatorial é o coeficiente de correlação entre a variável e o fator. Ela mostra a variância explicada pela variável naquele fator em particular.
Prosseguimos criando um objeto FactorAnalyzer com 6 fatores (tentativamente) e usando o método de rotação varimax.
# 6 fatores fa = FactorAnalyzer( 6, rotation="varimax") # o objeto tem o método fit para análise do dataframe fa.fit(df) # Desse extraimos as cargas fatoriais (factor loadings) # Observe que fa.loadings_ é um numpy.array com shape (25,6). Usamos o método # do pandas pd.DataFrame.from_records para convertê-lo em um dataframe factorLoadings = pd.DataFrame.from_records(fa.loadings_) # Para ver a dataframe gerado: factorLoadings.head(4)
| 0 | 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|---|
| 0 | 0.095220 | 0.040783 | 0.048734 | -0.530987 | -0.113057 | 0.161216 |
| 1 | 0.033131 | 0.235538 | 0.133714 | 0.661141 | 0.063734 | -0.006244 |
| 2 | -0.009621 | 0.343008 | 0.121353 | 0.605933 | 0.033990 | 0.160106 |
| 3 | -0.081518 | 0.219717 | 0.235140 | 0.404594 | -0.125338 | 0.086356 |
Vemos que os nomes dos itens, de A1 até O5, foram perdidos no cálculo. Vamos renomear tanto esses itens quanto os nomes das colunas (que são os fatores) para ter uma visualização mais clara do que obtivemos até aqui:
# Substitue as linhas pelo nomes dos itens
factorLoadings.index=itens
# Renomeia as colunas
factorLoadings.rename(columns = {0:'Fator 1',
1:'Fator 2',
2:'Fator 3',
3:'Fator 4',
4:'Fator 5',
5:'Fator 6'}, inplace = True)
# Exibe o resultado
factorLoadings
| Fator 1 | Fator 2 | Fator 3 | Fator 4 | Fator 5 | Fator 6 | |
|---|---|---|---|---|---|---|
| A1 | 0.095220 | 0.040783 | 0.048734 | -0.530987 | -0.113057 | 0.161216 |
| A2 | 0.033131 | 0.235538 | 0.133714 | 0.661141 | 0.063734 | -0.006244 |
| A3 | -0.009621 | 0.343008 | 0.121353 | 0.605933 | 0.033990 | 0.160106 |
| A4 | -0.081518 | 0.219717 | 0.235140 | 0.404594 | -0.125338 | 0.086356 |
| A5 | -0.149616 | 0.414458 | 0.106382 | 0.469698 | 0.030977 | 0.236519 |
| C1 | -0.004358 | 0.077248 | 0.554582 | 0.007511 | 0.190124 | 0.095035 |
| C2 | 0.068330 | 0.038370 | 0.674545 | 0.057055 | 0.087593 | 0.152775 |
| C3 | -0.039994 | 0.031867 | 0.551164 | 0.101282 | -0.011338 | 0.008996 |
| C4 | 0.216283 | -0.066241 | -0.638475 | -0.102617 | -0.143846 | 0.318359 |
| C5 | 0.284187 | -0.180812 | -0.544838 | -0.059955 | 0.025837 | 0.132423 |
| E1 | 0.022280 | -0.590451 | 0.053915 | -0.130851 | -0.071205 | 0.156583 |
| E2 | 0.233624 | -0.684578 | -0.088497 | -0.116716 | -0.045561 | 0.115065 |
| E3 | -0.000895 | 0.556774 | 0.103390 | 0.179396 | 0.241180 | 0.267291 |
| E4 | -0.136788 | 0.658395 | 0.113798 | 0.241143 | -0.107808 | 0.158513 |
| E5 | 0.034490 | 0.507535 | 0.309813 | 0.078804 | 0.200821 | 0.008747 |
| N1 | 0.805806 | 0.068011 | -0.051264 | -0.174849 | -0.074977 | -0.096266 |
| N2 | 0.789832 | 0.022958 | -0.037477 | -0.141134 | 0.006726 | -0.139823 |
| N3 | 0.725081 | -0.065687 | -0.059039 | -0.019184 | -0.010664 | 0.062495 |
| N4 | 0.578319 | -0.345072 | -0.162174 | 0.000403 | 0.062916 | 0.147551 |
| N5 | 0.523097 | -0.161675 | -0.025305 | 0.090125 | -0.161892 | 0.120049 |
| O1 | -0.020004 | 0.225339 | 0.133201 | 0.005178 | 0.479477 | 0.218690 |
| O2 | 0.156230 | -0.001982 | -0.086047 | 0.043989 | -0.496640 | 0.134693 |
| O3 | 0.011851 | 0.325954 | 0.093880 | 0.076642 | 0.566128 | 0.210777 |
| O4 | 0.207281 | -0.177746 | -0.005671 | 0.133656 | 0.349227 | 0.178068 |
| O5 | 0.063234 | -0.014221 | -0.047059 | -0.057561 | -0.576743 | 0.135936 |
Vamos montar mais um heatmap com essa tabela.
# A bibioteca seaborn já foi importada como sns plt.figure(figsize=(8,6)) sns.set(font_scale=.9) sns.heatmap(factorLoadings, linewidths=1, linecolor='#ffffff', cmap="YlGnBu", xticklabels=1, yticklabels=1)
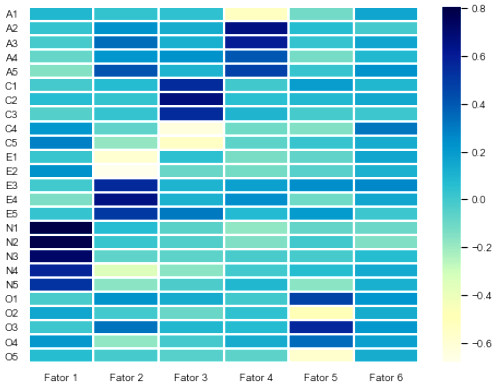
Lembrando que as cores mais escuras indicam correlação direta e as mais claras correlação inversa, percebemos que existem cargas mais fortes entre os itens N1, N2, N3, N4 e N5 com o fator 1, E1 até E5 no fator 2, etc. Nenhum dos itens, no entanto, tem carga relevante no sexto fator. Isso indica que podemos refazer o cálculo de cargas fatoriais com apenas 5 fatores.
# Refazendo o cáculo com 5 fatores apenas
# Apaga a variável fa
del fa
fa = FactorAnalyzer( 5, rotation="varimax")
fa.fit(df)
factorLoadings = pd.DataFrame.from_records(fa.loadings_)
# Renomeia itens
factorLoadings.index=itens
# Renomeia as colunas (fatores)
factorLoadings.rename(columns = {0:'Fator 1',
1:'Fator 2',
2:'Fator 3',
3:'Fator 4',
4:'Fator 5'}, inplace = True)
# Exibe o resultado
factorLoadings
| Fator 1 | Fator 2 | Fator 3 | Fator 4 | Fator 5 | |
|---|---|---|---|---|---|
| A1 | 0.111126 | 0.040465 | 0.022798 | -0.428166 | -0.077931 |
| A2 | 0.029588 | 0.213716 | 0.139037 | 0.626946 | 0.062139 |
| A3 | 0.009357 | 0.317848 | 0.109331 | 0.650743 | 0.056196 |
| A4 | -0.066476 | 0.204566 | 0.230584 | 0.435624 | -0.112700 |
| A5 | -0.122113 | 0.393034 | 0.087869 | 0.537087 | 0.066708 |
| C1 | 0.010416 | 0.070184 | 0.545824 | 0.038878 | 0.209584 |
| C2 | 0.089574 | 0.033270 | 0.648731 | 0.102782 | 0.115434 |
| C3 | -0.030855 | 0.023907 | 0.557036 | 0.111578 | -0.005183 |
| C4 | 0.240410 | -0.064984 | -0.633806 | -0.037498 | -0.107535 |
| C5 | 0.290318 | -0.176395 | -0.562467 | -0.047525 | 0.036822 |
| E1 | 0.042819 | -0.574835 | 0.033144 | -0.104813 | -0.058795 |
| E2 | 0.244743 | -0.678731 | -0.102483 | -0.112517 | -0.042010 |
| E3 | 0.024180 | 0.536816 | 0.083010 | 0.257906 | 0.280877 |
| E4 | -0.115614 | 0.646833 | 0.102023 | 0.306101 | -0.073422 |
| E5 | 0.036145 | 0.504069 | 0.312899 | 0.090354 | 0.213739 |
| N1 | 0.786807 | 0.078923 | -0.045997 | -0.216363 | -0.084704 |
| N2 | 0.754109 | 0.027301 | -0.030568 | -0.193744 | -0.010304 |
| N3 | 0.731721 | -0.061430 | -0.067084 | -0.027712 | -0.004217 |
| N4 | 0.590602 | -0.345388 | -0.178902 | 0.005886 | 0.075225 |
| N5 | 0.537858 | -0.161291 | -0.037309 | 0.100931 | -0.149769 |
| O1 | -0.002224 | 0.213005 | 0.115080 | 0.061550 | 0.504907 |
| O2 | 0.175788 | 0.004560 | -0.099729 | 0.081809 | -0.468925 |
| O3 | 0.026736 | 0.310956 | 0.076873 | 0.126889 | 0.596007 |
| O4 | 0.220582 | -0.191196 | -0.021906 | 0.155475 | 0.369012 |
| O5 | 0.085401 | -0.005347 | -0.062730 | -0.010384 | -0.533778 |
Construimos o heatmap com essa tabela de 5 fatores.
plt.figure(figsize=(8,6)) sns.set(font_scale=.9) sns.heatmap(factorLoadings, linewidths=1, linecolor='#ffffff', cmap="YlGnBu", xticklabels=1, yticklabels=1)

Pelo heatmap percebemos que o grupo de itens N está associado ao fator 1 (Neuroticismo), E ao fator 2 (Extroversão), C ao fator 3 (Conscienciosidade), A ao fator 4 (Amabilidade) e O ao fator 5 (Abertura), previamente identificados. É claro que essa identificação do fator foi realizada pelos pesquisadores no caso dessa pesquisa em particular. Para uma pesquisa nova seria necessário um estudo para o entendimento da natureza de cada fator.
Observe ainda que correlação negativa é correlação. É o que ocorre, por exemplo entre os itens A1 (Sou indiferente aos sentimentos das outras pessoas) e A2 (Sempre pergunto sobre o bem-estar dos outros). A correlação entre eles pode ser obtida da matriz de correlação, corrMatriz['A1']['A2'] = -0.35091.
Observamos que existem as seguintes correspondências entre os grupos de questões e os fatores propostos:
| Fator | Grupo | Descrição |
|---|---|---|
| 1 | N | Neuroticismo |
| 2 | E | Extroversão |
| 3 | C | Conscienciosidade |
| 4 | A | Amabilidade |
| 5 | O | Abertura |
Vamos, portanto, renomear as colunas de nossa matriz de cargas fatoriais para refletir esse entendimento:
# Renomeia as colunas (fatores)
factorLoadings.rename(columns = {'Fator 1':'Neuroticismo',
'Fator 2':'Extroversão',
'Fator 3':'Conscienciosidade',
'Fator 4':'Amabilidade',
'Fator 5':'Abertura'}, inplace = True)
# Exibe o resultado (só duas linhas)
factorLoadings.head(2)
| Neuroticismo | Extroversão | Conscienciosidade | Amabilidade | Abertura | |
|---|---|---|---|---|---|
| A1 | 0.111126 | 0.040465 | 0.022798 | -0.428166 | -0.077931 |
| A2 | 0.029588 | 0.213716 | 0.139037 | 0.626946 | 0.062139 |
Comunalidades são a soma das cargas fatoriais ao quadrado de cada variável medida. Denotando por \(l_{ij}\) os elementos da matriz da cargas fatoriais a comunalidade da i-ésima variável é \(h_i^2\) dado por
$$
h_i^2 =\Sigma_{j=1}^n l_{ij}^2
$$
Por exemplo, a comunalidade relativa à questão A1 é a soma dos elementos (ao quadrado) da primeira linha da matriz de cargas fatoriais acima:
(0.111126)**2 + (0.040465)**2 + (0.022798)**2 + (-0.428166)**2 +(-0.077931)**2
As comunalidades relativas a todas as variáveis podem ser obtidas com get_communalities() que retorna um numpy.ndarray com dimensões (25,):
fa.get_communalities()
A soma de todos os valores de comunalidade é o valor de comunalidade total:
fa.get_communalities().sum()
Para exibir uma tabela com os nomes da variáveis e suas respectivas comunalidades vamos construir um dataframe contendo esses dados. Lembrando que já temos a variável itens = ['A1', 'A2', ..., 'O4','O5']:
dfComunalidades = pd.DataFrame(comunalidades) dfComunalidades.index = itens
| Variável | Comunalidade |
|---|---|
| A1 | 0.203905 |
| A2 | 0.462803 |
| A3 | 0.539692 |
| A4 | 0.301905 |
| A5 | 0.470020 |
| C1 | 0.348395 |
| C2 | 0.453872 |
| C3 | 0.324289 |
| C4 | 0.476699 |
| C5 | 0.435383 |
| Variável | Comunalidade |
|---|---|
| E1 | 0.347809 |
| E2 | 0.545502 |
| E3 | 0.441055 |
| E4 | 0.541257 |
| E5 | 0.407146 |
| N1 | 0.681398 |
| N2 | 0.608003 |
| N3 | 0.544475 |
| N4 | 0.505803 |
| N5 | 0.349316 |
| Variável | Comunalidade |
|---|---|
| O1 | 0.317339 |
| O2 | 0.267452 |
| O3 | 0.474643 |
| O4 | 0.246035 |
| O5 | 0.296284 |
| Total | 10.5905 |
| Como temos 25 fatores: | |
| Total/25 | 0.4236 |
Podemos pensar na comunalidade de uma variável como a proporção de variação nessa variável explicada pelos fatores propostos no modelo. Por exemplo, a variável N1 tem a maior comunalidade (0.681398) nesse modelo, indicando que aproximadamente 69% da variação nas respostas para “N1: Fico com raiva facilmente” é explicada pelo modelo de 5 fatores proposto enquanto esse valor é de apenas 20% para “A1: Sou indiferente aos sentimentos das outras pessoas”.
Comunalidades servem para avaliar o desempenho do modelo. Valores mais próximos de um indicam que o modelo explica a maior parte da variação para essas variáveis. Nesse caso o modelo está melhor ajustado para as variáveis do grupo N (neuroticismo) e menos eficiente para as variáveis do grupo O (abertura).
A Comunalidade total é de 10.5905 que, dividido entre as 25 variáveis indica uma média de 10.5905/25 = 0.4236 geral para o modelo, ou seja, uma eficiência média de 42% do modelo em explicar a variação de cada variável do teste.
 Já em 1489 os sinais \( + \mbox{ e } –\) aparecem em uma obra sobre aritmética comercial de João Widman d’Eger, publicada em Leipzig, Alemanha. Eles não se referiam, no entanto, às representações de soma e subtração, ou à números positivos ou negativos, mas a excessos e déficit em problemas sobre operações comerciais. Os símbolos para positivos e negativos só se difundiram na Inglaterra com o uso feito por Robert Recorde em 1557. Os mesmos sinais já eram usados anteriormente, como exemplifica o pintura destes sinais em barris para indicar se estavam ou não cheios. Os gregos antigos, como Diofanto, por exemplo, indicavam a soma por justaposição das parcelas, assim como ainda é feito no caso de frações, \(1^{1/2}\), por exemplo. Os algebristas italianos usavam a palavra latina plus, ou sua letra \(p\) inicial, para indicar a operação de soma.
Já em 1489 os sinais \( + \mbox{ e } –\) aparecem em uma obra sobre aritmética comercial de João Widman d’Eger, publicada em Leipzig, Alemanha. Eles não se referiam, no entanto, às representações de soma e subtração, ou à números positivos ou negativos, mas a excessos e déficit em problemas sobre operações comerciais. Os símbolos para positivos e negativos só se difundiram na Inglaterra com o uso feito por Robert Recorde em 1557. Os mesmos sinais já eram usados anteriormente, como exemplifica o pintura destes sinais em barris para indicar se estavam ou não cheios. Os gregos antigos, como Diofanto, por exemplo, indicavam a soma por justaposição das parcelas, assim como ainda é feito no caso de frações, \(1^{1/2}\), por exemplo. Os algebristas italianos usavam a palavra latina plus, ou sua letra \(p\) inicial, para indicar a operação de soma.
O sinal \(\times\), indicador de um produto, é relativamente moderno. Oughtred foi o primeiro a usá-lo em seu livro Clavis Matematicae, publicado em 1631. No mesmo ano, Harriot usou um ponto entre os fatores. Em 1637 Descartes usou a pura justaposição dos termos para indicar seu produto. Nos textos mais antigos de Leibniz encontra-se o sinal \(\cap\) para indicar multiplicação e \(\cup\) para a divisão. Mais tarde ele introduziu o ponto como um símbolo para a multiplicação e dois pontos (\(:\)) para a divisão. O sinal \(\div\), segundo Rouse Ball, resultou de uma combinação de dois sinais existentes “-” e “:”. As formas \(a/b\) ou \(\frac{a}{b}\) são atribuídas aos árabes.
Na Idade Média a igualdade entre dois termos é indicada literalmente por aequalis, do latim, ou através da abreviatura est. Xulander, matemático alemão do século XVI indicava a igualdade por dois pequenos traços paralelos verticais, ||,
 O símbolo \(\infty\) para o infinito foi introduzido por John Wallis (1616-1703) em seu livro De sectionibus conicis (Sobre as seções cônicas, 1655 ). Wallis era um estudioso clássico com grande erudição e é possível que tenha se inspirado no sinal romano para o número 1000, escrito CD ou M. Também se cogita que ele tenha tido esta idéia a partir da última letra do alfabeto grego, o ômega grego minúsculo, \(\omega\), como uma metáfora para o limite superior, o fim.
O símbolo \(\infty\) para o infinito foi introduzido por John Wallis (1616-1703) em seu livro De sectionibus conicis (Sobre as seções cônicas, 1655 ). Wallis era um estudioso clássico com grande erudição e é possível que tenha se inspirado no sinal romano para o número 1000, escrito CD ou M. Também se cogita que ele tenha tido esta idéia a partir da última letra do alfabeto grego, o ômega grego minúsculo, \(\omega\), como uma metáfora para o limite superior, o fim.
Os símbolos para a operação de derivação, \(dx,\, dy\) e \(dx/dy\) foram propostos por Leibniz em um manuscrito de novembro de 1675. Newton usava a notação de fluxos \(\dot x, \dot y, \dot x /\dot y\). Esta notação é ainda usada amplamente em textos de mecânica quando a trajetória de uma partícula aparece sob forma paramétrica. Por exemplo, se descrevemos a trajetória de uma partícula por meio de sua posição vetorial \(\vec{r}(t)= \left(x(t), y(t), z(t)\right)\) então sua velocidade será escrita como \(\vec{v}(t)= \left(\dot x(t), \dot y(t), \dot z(t)\right)\).

Os símbolos \(f'(x)\) e \(f”(x)\) para as derivadas de primeira e segunda ordem respectivamente foram usados primeiro por Lagrange. Em Théorie des Fonctions Analytiques, 1797, se lê simplesmente \(f’x\) e \(f”x\), símbolos revisados mais tarde para incluir os parênteses que envolvem o argumento da função. Em 1770 Lagrange empregou \(\phi’=d\phi/dx\), omitindo por completo o argumento quando ele estava claro pelo contexto e, em 1772, \(u’=du/dx\) e \(du=u’dx\). O símbolo \(D_x y\) foi usado por Louis François Antoine Arbogast (1759-1803) em De Calcul des dérivations et ses usages dans la théorie des suites et dans le calcul différentiel.
Um delta grego maiúsculo, \(\Delta\), para indicar uma quantidade pequena ou a diferença entre funções foi usado em 1706 por Johann Bernoulli. O símbolo \(\partial\), “d curvo ”, apareceu em 1770 por sugestão de Antoine Nicolas Caritat (1743-1794) em um livro sobre equações diferenciais parciais para representar diferenciais parciais \(\partial f\), em oposição às diferencias totais \(df\). A forma \(\frac{\partial u}{\partial x}\) só foi empregada em 1786 por Legendre em um texto sobre máximos e mínimos associados ao cálculo das variações. Legendre abandonou o uso deste símbolo, só recuperado mais tarde por Jacobi em 1841. O símbolo \(\partial\) corresponde à letra dey cursiva no alfabeto Cirílico.
 Para representar a integração Leibniz escrevia, no início de seu desenvolvimento, a palavra latina omnia (tudo) em frente à quantidade a ser integrada. Depois passou a escrever \(dx\) após a integração e, em carta de 1675 para Oldenburg, secretário da Royal Society, ele sugeriu o uso de \(\int\), uma degeneração de um S longo significando summa (soma). Em Quadratura curvarum, 1704, Newton usou uma pequena barra vertical \(\overline x\) para representar \(\int x dx\). Duas barras verticais paralelas, \(\overline {\overline x}\) indicava a integração dupla. Em outras ocasiões ele escrevia o termo a ser integrado dentro de um retângulo. As convenções de Newton, como se pode imaginar, davam margem a erros de interpretação e nunca se tornaram populares, nem mesmo entre seus seguidores diretos na Inglaterra.
Para representar a integração Leibniz escrevia, no início de seu desenvolvimento, a palavra latina omnia (tudo) em frente à quantidade a ser integrada. Depois passou a escrever \(dx\) após a integração e, em carta de 1675 para Oldenburg, secretário da Royal Society, ele sugeriu o uso de \(\int\), uma degeneração de um S longo significando summa (soma). Em Quadratura curvarum, 1704, Newton usou uma pequena barra vertical \(\overline x\) para representar \(\int x dx\). Duas barras verticais paralelas, \(\overline {\overline x}\) indicava a integração dupla. Em outras ocasiões ele escrevia o termo a ser integrado dentro de um retângulo. As convenções de Newton, como se pode imaginar, davam margem a erros de interpretação e nunca se tornaram populares, nem mesmo entre seus seguidores diretos na Inglaterra.
Os limites de integração eram inicialmente indicados por palavras, não existindo um simbolismo para os designar. Euler foi o primeiro a sugerir o uso de uma notação específica, escrevendo os limites entre colchetes e escrevendo as palavras latinas ab e ad. Fourier deu a forma atual, escrevendo \(\int_a ^b f(x)dx\) para representar a integral definida, com \(x\) variando de \(a\) até \(b\). Este símbolo apareceu em um artigo da Memórias da Academia Francesa, 1819-20, reimpresso em Théorie analytique de la chaleur, 1822. O símbolo \(\oint\) para representar a integração sobre um caminho fechado parece ter sido usado pela primeira vez em 1917 por Arnold Sommerfeld (1868-1951) no periódico Annalen der Physik.
A notação de limites foi apresentada em 1786 por Simon Antoine Jean L’Huilier (1750-1840). Em seu Exposition élémentaire des principles des calculs superieurs ele escreveu: “… para resumir e facilitar o cálculo por meio de uma notação mais cômoda é conveniente escrever
$$\lim . \frac{\nabla P}{\nabla x}$$
o limite das variações simultâneas de \(P\) e de \(x\) em lugar de
$$\lim . \frac{dP}{dx},$$
de forma que as duas expressões significavam a mesma coisa. Observe que L’Huilier escrevia \(\lim\)., usando um ponto após o limite. Karl Weierstrass (1815-1897) adotou esta notação, abandonando o ponto.
Cauchy usou a letra grega epsilon, \(\epsilon\) ou \(\varepsilon\) em 1821 em Cours d’analyse, embora também usasse às vezes a letra delta, \(\delta\). Alguns autores sugerem que delta significa “ différence ” (diferença) enquanto epsilon significa ” erreur ” (erro). A primeira prova de Cauchy usando epsilons e deltas é basicamente o teorema do valor intermediário para as derivadas. Na demonstração ele traduz sua definição de que a derivada é um limite do quociente das diferenças, quando este limite existe, em linguagem algébrica usando epsilons e deltas. No entanto ele não estabelece uma relação entre \(\epsilon\) e \(\delta\), não fazendo portanto distinção entre convergência uniforme ou pontual.
O operador diferencial \(\nabla\) (nabla ou del) foi introduzido por William Rowan Hamilton (1805-1865). Inicialmente Hamilton usou este símbolo para representar uma função arbitrária, depois como o operador de permutações. Em 1846 Hamilton usou nabla, desenhado horizontalmente, como o operador diferencial vetorial. Maxwell e Riemann usavam a abreviatura grad para representar o gradiente. William Clifford (1845-1879) incorporou o termo divergência que denotava por \(\mbox{div }u\) ou \(\mbox{dv }u\). O símbolo \(\nabla ^2\) para representar o operador laplaciano foi proposto por Robert Murphy em 1883.
Devemos observar, como conclusão, que a notação usada para descrever um conceito em matemática é completamente arbitrária, não passando de convenções que podem, em princípio, ser totalmente alteradas. No entanto, temos que aprender com Leibniz que o estabelecimento de uma notação compacta, simples e de fácil leitura e manipulação é essencial para o desenvolvimento e uso de uma teoria. Além disto a padronização é essencial para que os conceitos sejam facilmente transmitidos e o ensino da disciplina seja simplificado. Com frequência, na história da matemática, uma nova teoria ou a demonstração de uma conjectura é proposta de forma obscura e de difícil leitura, sendo acessível apenas a um círculo restrito de especialistas na área. Mais tarde, dependendo da generalidade e aplicabilidade da inovação ela passa por uma série de alterações, encontrando formas mais didáticas e claras de exposição e reunindo argumentações de mais fácil acesso para a comunidade mais geral. Eventualmente, em geral após a depuração e aprimoramento teórico, a novidade surge nos livros textos e é incorporada nos currículos de ensino.

Os professores de matemática hoje se deparam com uma tarefa difícil: a motivação de seus alunos para os tópicos mais áridos desta ciência. Este problema tem diversas causas que vão desde os problemas com a qualidade geral do ensino até, por exemplo, a crença de que “está tudo pronto”, de que nada mais resta a desenvolver ou a descobrir. É comum ouvir reclamações de que um determinado cálculo pode ser realizado rapidamente em um computador e que, portanto, não seria necessário aprender a utilizar aquela técnica. No entanto sabemos que a tecnologia progride a passos rápidos e que o volume de artigos e novas idéias científicas nunca foi tão grande como hoje. Por isto, procurando contribuir para um melhor entendimento de nosso propósito como professores e estudantes de matemática, me proponho perguntar: por que devemos estudar matemática? Para que serve, afinal, a matemática?

Em primeiro lugar a matemática serve para descrever o mundo de uma forma rigorosa e precisa. Ela é uma linguagem, uma parte essencial na formação de modelos. Um modelo é um conjunto de definições e conceitos que busca descrever de maneira tão completa e fidedigna quanto possível o mundo natural ou uma parte dele, ou ainda processos artificiais criados pela crescente complexidade dos relacionamentos humanos. Esses modelos, além de serem tão completos quanto possível e possuírem coerência lógica, devem ser testados, comparados com o sistema real que ele pretende descrever por meio da observação ou da experimentação. Em caso de disparidades entre a descrição e a observação empírica o modelo deverá ser refeito e aperfeiçoado, ou mesmo abandonado se necessário.
Modelos são representações e não o objeto ou sistema de objetos descritos. Eles podem ser muito simples, como o modelo que representa o conjunto dos números naturais, {1, 2, 3, …}. Estes números foram usados, entre outras coisas, para contar quantas cabeças de gado um homem primitivo tinha e como ele poderia troca-las por alimentos ou outros bens. Nesta contagem ele pode ter usado pedrinhas (daí a palavra cálculo) para representar seus animais, estabelecendo uma relação biunívoca entre animais e pedras. Se possuía menos que uma dezena de bois e vacas, é possível que tenha usado apenas os dedos das mãos (de onde surgiu a palavra dígito). Embora simples este modelo não é trivial. É possível representar com um número natural quantos grãos de areia existem na Terra? (A resposta é sim!) E, principalmente, este modelo é incompleto.
Se pretendermos que nossas negociações incluam dívidas (e, como consequência, o calote!) teremos que expandir o modelo de forma a abarcar os números negativos e o zero, resultando no conjunto dos inteiros. O conjunto dos inteiros é ainda menos óbvio e mais abstrato que o dos naturais pois não temos conhecimento de alguma coisa concreta que exista em quantidades negativas! E mesmo este novo conjunto não é completo e não suficiente. Se quisermos oferecer como parte dos negócios uma fração de um terreno ou um pedaço de um queijo gigante teremos que ampliar o conjunto dos inteiros para outro conjunto que contenha frações, o conjunto dos racionais.

Esse parece agora ser um conjunto bem bonito e completo, o conjunto dos racionais, não tivessem os gregos descoberto que alguns números importantes não se encaixam dentro deles. A diagonal de um quadrado cujos lados medem um (em qualquer sistema de unidades) não é um racional e nem a razão entre a circunferência e o raio de um círculo (igual a 2 pi) não são números racionais. A experiência e a necessidade de descrever coisas pedem um modelo mais amplo. Por isto surgiram os irracionais, os números que não podem ser postos sob forma de uma fração. Racionais e irracionais, juntos, formam o conjunto dos números reais.
Estamos agora, a esta altura do desenvolvimento dos modelos matemáticos, muito longe dos conceitos intuitivos e primários. O conjunto dos números reais possui propriedades intrigantes e muito pouco óbvias. Entre dois números reais quaisquer existe uma infinidade de outros reais. Sua representação gráfica, a reta real, é infinita em ambas as direções e os pontos se empacotam de forma perfeita sem deixar nenhum furo ou imperfeição. O conceito é extremamente poderoso, possui coerência lógica e serve como modelo para a descrição de grande quantidade de objetos do mundo real. No entanto, não é tão claro se existe qualquer objeto no universo real que seja um bom representante desse modelo. Ele é útil para fazer descrições aproximadas de objetos que existem: se medirmos a distância entre duas cidades ou o comprimento de um fio estaremos ignorando, de forma totalmente apropriada e válida, as imperfeições do fio e da estrada que certamente não são contínuos como a reta real. Se ampliarmos com um potente microscópio uma seção do fio, veremos que ele, sendo de metal, é feito de granulações bem organizadas apresentando grandes vãos entre os átomos de sua estrutura. Isto não nos impedirá, no entanto, de usar réguas comuns para medir seu comprimento.
Observamos aqui uma tendência. O conjunto dos reais engloba os racionais, que por sua vez engloba os inteiros, que contém os naturais. O progresso do conhecimento se dá na direção da ampliação dos conceitos e na quebra das antigas barreiras. E, diferente do que se costuma pensar, os conceitos antigos, desde que bem estabelecidos, não são revogados como se revoga uma lei caduca e sim ampliados no que diz respeito a seu domínio de aplicação. Uma observação importante deve ser acrescentada aqui. Neste ponto do desenvolvimento da matemática (e mesmo antes disto, na verdade!), e da civilização humana como um todo, já teremos a necessidade de escolas. Precisaremos tirar as crianças de seus brinquedos e colocá-las em salas de aulas para garantir que o conhecimento acumulado por gerações de estudiosos, teóricos ou pessoas pragmáticas e engenhosas, seja repassado para as novas gerações. E, na medida em que cresce o domínio da ciência e as exigências das aplicações, mais tempo as pessoas deverão se dedicar ao estudo e a preparação para seu desempenho na vida e no ambiente de trabalho. Este é o preço que pagamos por termos descido das árvores e começado a usar ossos como ferramentas, modelar pedras para servir como instrumentos e armas, aprendido a domesticar o fogo.
Os modelos, é claro, passaram a representar objetos de complexidade crescente. Na planilha do engenheiro um prédio é um modelo de equilíbrio de forças onde a matemática permite que os pesos, as tensões no concreto e nos ferros se equilibrem para deixar estável a construção. Podemos descrever como se comporta uma mola mergulhada em um meio viscoso e sujeita a impactos externos, exatamente como existe no sistema de molas e amortecedores de um automóvel. O sistema é simples mas sua descrição completa exige um tópico matemático sofisticado, o das equações diferenciais. Queremos saber como uma corrente de elétrons se move dentro de materiais semicondutores. Para isto precisamos de um modelo bastante elaborado da física, a mecânica quântica. Com ela construímos relógios digitais, computadores e discos rígidos, entre outras máquinas diversas.
Grande parte das pessoas hoje, exceto aqueles excluídos da modernidade pela pobreza, usa direta ou indiretamente um satélite artificial para telecomunicações colocado em órbita geo-estacionária. Esses satélites giram em torno de nosso planeta com uma velocidade tal que parecerá, para um observador fixo na terra ou para a antena de seu receptor de TV, como estacionário em pleno ar. Para colocar um artefato desses em órbita é necessário usar o modelo da gravitação universal criado por Newton e, em alguns casos, será até mesmo necessário fazer correções usando o modelo da relatividade de Albert Einstein. Muita matemática está envolvida e provavelmente computadores sofisticados serão empregados nessas operações.
 Exemplos de modelos mais prosaicos, mas igualmente úteis, podem ser encontrados na economia, no estudo das variações de preços dos produtos oferecidos ao consumidor, da inflação, do valor de um depósito feito meses atrás na caderna de poupança ou outra aplicação mais rentável. Modelos análogos serão usados para compreender a disseminação de uma doença, o contágio por um vírus ou a divulgação de um boato. Um modelo pode ser simples, como aquele que descreve os valores disponíveis em uma aplicação bancária com rendimento fixo, ou complicado e extenso como seria o modelo, ainda não desenvolvido, que descreve as oscilações nas bolsas de valores.
Exemplos de modelos mais prosaicos, mas igualmente úteis, podem ser encontrados na economia, no estudo das variações de preços dos produtos oferecidos ao consumidor, da inflação, do valor de um depósito feito meses atrás na caderna de poupança ou outra aplicação mais rentável. Modelos análogos serão usados para compreender a disseminação de uma doença, o contágio por um vírus ou a divulgação de um boato. Um modelo pode ser simples, como aquele que descreve os valores disponíveis em uma aplicação bancária com rendimento fixo, ou complicado e extenso como seria o modelo, ainda não desenvolvido, que descreve as oscilações nas bolsas de valores.
Tais modelos são úteis no presente, essenciais para a manutenção da vida moderna, complexa como ela se tornou. Mas eles têm uma habilidade extra: nos permitem prever o futuro. Um bom modelo descreve o que existe hoje e aponta para o que existirá amanhã, mesmo que esta previsão só possa ocorrer em termos probabilísticos, em alguns casos.
Um astrônomo poderá ver hoje em seu telescópio uma grande pedra varrendo o espaço em grande velocidade e decidir, usando os modelos matemáticos à sua disposição, se esta pedra colidirá ou não com nosso planeta. Como exemplo, a colisão do asteróide Shoemaker-Levi com o planeta Júpiter foi prevista com grande antecedência. Um bom modelo estelar será hábil para dizer, supondo conhecidas as condições atuais da estrela, em que estágio de sua evolução ela se encontra e por que etapas passará no futuro. Podemos, é claro, optar por uma visão poética dessa mesma estrela e isto será, sem dúvida, muito bom de se fazer. Mas, teremos perdido a habilidade de descobrir que essa estrela terá um dia esgotado seu combustível nuclear, que explodirá e poderá se tornar um buraco negro.
Finalmente chegamos àquela que considero ser a utilidade mais fina e essencial da matemática. Supridas as necessidades básicas do ser humano, garantida sua sobrevivência, seu anseio pela procriação e preservação da espécie e seu nível mínimo de conforto, a mente se volta para o conhecimento pelo conhecimento. Em um nível mais refinado não tem sentido perguntar para que serve a matemática. Por um lado um teorema serve porque é correto, porque é uma verdade. Por outro lado inúmeras teorias matemáticas foram desenvolvidas de forma puramente acadêmica, ou filosóficas, e muito mais tarde foram usadas em aplicações espetaculares.
Chegamos hoje a um estado de desenvolvimento da civilização onde a diversidade parece ser essencial. Precisamos de técnicos, de mão-de-obra braçal, de teóricos e de filósofos para enfrentar os desafios múltiplos e prementes por que passamos hoje. Um exemplo simples pode ser dado para corroborar esta afirmação: um pouco de ética bastaria para resolver grande parte das mazelas em nosso pais e conflitos pelo mundo afora e, neste sentido, precisamos de cidadãos filósofos. A experiência da história mostra que os povos que fizeram uso puramente pragmático da matemática entraram, ou já estavam, em declínio, enquanto os tempos áureos de qualquer povo, como na Grécia clássica, foram sempre pontuados pela livre investigação em todas as áreas a eles acessíveis, particularmente na matemática.
Vivemos em um período extraordinário da história da civilização. Temos hoje a habilidade para construir modelos científicos que descrevem o universo globalmente, que lançam perguntas sobre sua origem e destino e apontam para suas respostas. Estamos desvendando o código primário da existência humana através do projeto Genoma. Por outro lado, possuímos armas de destruição em massa e o poder para alterar de forma radical o clima no planeta. Os meios de transporte e as telecomunicações estão destruindo as barreiras nacionais e este processo não é suave ou indolor, particularmente para as nações mais pobres e com desenvolvimento tecnológico pouco consolidado.
A inserção em um mundo sem fronteiras exige profissionais de primeira linha, com formação simultaneamente profunda e ampla. Refletir sobre o avanço da ciência e da tecnologia, sobre os problemas que ela resolve e outros que ela causa, e participar deste progresso é essencial para que a sociedade brasileira possa se inserir na cidadania global em nível de igual participação e oportunidade.

O conceito de conjuntos é um conceito primário, básico ao entendimento de toda a matemática. Conjuntos são coleções de objetos, não necessariamente envolvendo números ou outra entidade matemática. Podemos representar um conjunto exibindo explicitamente seus elementos. É o que fazemos mostrando os naipes de cartas de baralho:
$$ C_{1}=\{\spadesuit,\clubsuit,\diamondsuit,\heartsuit\}, $$
ou o conjunto dos inteiros ímpares menores que 10:
$$ C_{2}=\{1,3,5,7,9\}. $$
Outra forma útil consiste em descrever o conjunto usando a notação:
$$ \text{Conjunto } =\{x_i|\; \text{ alguma propriedade satisfeita pelos elementos} \}.$$
Em muitas situações o conjunto pode ser muito grande ou possuir infinitos elementos, de forma que não podemos explicitá-los uma a um. É o que ocorre com o conjunto dos inteiros pares
$$ C_{3}=\{ \left.n_i \in \mathbb{N}\right|n_i \,\,\text{ os inteiros pares}\} = \{ 2n_i | n_i \in \mathbb{Z} \} $$
$$ C_{3}=\{n_i \in \mathbb{N} | n_i \,\text{ um inteiro par} \} = \{ 2n_i | n_i \in \mathbb{Z} \}, $$
ou o conjunto de pontos no plano \(\mathbb{R}^2\) sobre a circunferência de raio 1,
$$ C_{4}=\{\left.(x,\,y)\in\mathbb{R}^2\right|(x^2+y^2=1)\}. $$
Se os elementos de um conjunto podem ser contados ele é dito enumerável e sua ordem, que denotaremos por \(\text{ord}(A)=n\), é o número de seus elementos. Nos exemplos acima temos \(\text{ord}(C_{1})=4\), \(\text{ord}(C_{2})=5\). O conjunto \(C_{3}\) é enumerável, com infinitos elementos, e \(C_{4}\) não é enumerável (também possuindo infinitos elementos).
Dizemos que um elemento \(a\) pertence à um conjunto \(C\) se \(a\) é um dos elementos de \(C\). Denotamos esta relação por \(a\in C\). Caso contrário escrevemos \(a\notin C\).
Dizemos que um conjunto \(A\) está contido no conjunto \(B\) se todos os elementos de \(A\) estão também em \(B\). Denotamos esta relação por \(A\subset B\). Caso contrário escrevemos \(A\not\subset B\). Observe que vale a seguinte afirmação: se \(A\subset B\) e \(x\in A\Rightarrow x\in B.\)


Conjuntos podem ser combinados de várias maneiras. Por exemplo, se \(A\) e \(B\) são dois conjuntos podemos encontrar a união dos dois, \(A\cup B\), ou sua intersecção \(A\cap B\), ilustradas na figura 1. Observe que
$$ x\in A\cup B \Rightarrow x\in A\text{ ou }x\in B, $$
$$ x\in A\cap B \Rightarrow x\in A\text{ e }x\in B. $$
Um número maior de conjuntos podem também ser combinados. Se \(A_{i}\) é uma coleção de conjuntos (\(i=1,\ldots,\,n)\) denotamos a união e intersecção destes conjuntos por: \(\underset{i=1}{\cup}A_{i}, \underset{i=1}{\cap}A_{i},\) respectivamente.  Observe que dois conjuntos são disjuntos se \(A\cap B=\emptyset\).
Observe que dois conjuntos são disjuntos se \(A\cap B=\emptyset\).
Definição: Se \(A\subset S\) definimos \(\bar{A},\) o complementar de \(A,\) como o conjunto de todos os elementos de \(S\) que não estão em \(A\),
 $$ \bar{A}=\{x\in S;\,\,x\notin A\}. $$
$$ \bar{A}=\{x\in S;\,\,x\notin A\}. $$
Observe que \(A\cup\bar{A}=S\).
Se \(S\) é finito ou numerável com \(n\) elementos então existem \(2^{n}\) eventos associados (subconjuntos de \(S\)).
O produto externo é outra forma de combinar conjuntos:
$$ A\times B=\left\{ (a,b)|a\in A,b\in B\right\}. $$
Seus elementos são os pares ordenados \((a,b)\). Observe que \(\mathbb{R}^n = \mathbb{R}\times\ldots\times\mathbb{R}.\)
 Um experimento é não determinístico ou aleatório se seu resultado não pode ser determinado previamente, à partir das condições iniciais do sistema usado. Na prática um experimento pode ser considerado aleatório se o conjunto das condições iniciais e sua evolução até a obtenção do resultado forem muito complexas e de difícil análise. Por exemplo, quando se atira uma moeda todas as leis envolvidas no movimento são causais e é possível prever o resultado (com que face ela cairá ao solo) se todas as condições iniciais forem conhecidas. No entanto estas condições envolvem um grande número de variáveis (tais como as colisões com partículas do ar) e é, quase sempre, mais apropriado considerar que o resultado será aleatório. Na natureza macroscópica poucos experimentos são realmente aleatórios. No nível microscópico (quântico) temos fenômenos completamente aleatórios, tais como o momento em que uma substância radioativa sofrerá um decaimento e emitirá uma partícula ou radiação.
Um experimento é não determinístico ou aleatório se seu resultado não pode ser determinado previamente, à partir das condições iniciais do sistema usado. Na prática um experimento pode ser considerado aleatório se o conjunto das condições iniciais e sua evolução até a obtenção do resultado forem muito complexas e de difícil análise. Por exemplo, quando se atira uma moeda todas as leis envolvidas no movimento são causais e é possível prever o resultado (com que face ela cairá ao solo) se todas as condições iniciais forem conhecidas. No entanto estas condições envolvem um grande número de variáveis (tais como as colisões com partículas do ar) e é, quase sempre, mais apropriado considerar que o resultado será aleatório. Na natureza macroscópica poucos experimentos são realmente aleatórios. No nível microscópico (quântico) temos fenômenos completamente aleatórios, tais como o momento em que uma substância radioativa sofrerá um decaimento e emitirá uma partícula ou radiação.
O conjunto dos resultados possíveis para um dado experimento é denomidado seu espaço amostral. Denotaremos por \(\varepsilon\) os experimentos e \(S\) seu espaço amostral. Alguns exemplos de experimentos aleatórios (dentro das ressalvas dadas acima) são:
\(\varepsilon_{1}:\) Jogue uma moeda 4 vezes e observe número de caras resultantes. \(S=\{0,1,2,3,4\} \).
\(\varepsilon_{2}:\) Jogue uma moeda 4 vezes e verifique a sequência de caras (que denotaremos por h) e coroas (que denotaremos por t). \(S=\{ \text{(hhhh), (hhht), …, (tttt)}\} \).
\(\varepsilon_{3}:\) Jogue uma moeda 4 vezes e verifique quantas caras e coroas resultam. \(S=\{(0,4),\,(1,3),\,(2,2),\,(3,1),\,(4,0)\} \).
\(\varepsilon_{4}:\) Deixe uma lâmpada acesa até queimar. Verifique o tempo de vida da lâmpada (um espaço amostral contínuo).
\(\varepsilon_{5}:\) Em um lote com 10 peças, sendo 3 defeituosas, retire 1 de cada vez, sem repor, até que todas com defeito sejam removidas. Quantas peças serão retiradas? \(S=\{3,4,5,6,7,8,9,10\}\).
\(\varepsilon_{5′}:\) Mesmo experimento anterior. Quantas peças podem ser retiradas sem que alguma tenha defeito? \(S=\{1,2,3,4,5,6,7\}\).
Definição: Um evento relativo ao experimento \(\varepsilon\) é um subconjunto de \(S\).
Exemplo 1: São eventos associados aos experimentos já listados:
\(\varepsilon_1\): \(A=\{2\} ,\) duas caras ocorrem,
\(\varepsilon_3\): \(B=\{(3,1),\,(4,0)\}\), mais caras que coroas,
\(\varepsilon_4\): \(C=\{t |\, t \lt 3000h \}\), lâmpada queima antes de 3000 horas.
Observe que, com esta definição, \(S\) e \(\emptyset\) são ambos eventos.
Se \(A\) e \(B\) são eventos então também são eventos:
| \(A\cup B\) | ocorre se \(A\) ou \(B\) ocorrem, |
| \(A\cap B\) | ocorre se \(A\) e \(B\) ocorrem, |
| \(\bar{A}\) | ocorre se \(A\) não ocorre. |
No caso de diversos eventos \(A_{i}\) associados ao experimento:
| \(\underset{i}{\cup}A_{i}\) | ocorre se um dos \(A_i\) ocorre, |
| \(\underset{i}{\cap}A_{i}\) | ocorre se todos os \(A_i\) ocorrem. |

Notação: Se um experimento consiste na execução do experimento \(\varepsilon\) \(n\) vezes denotamos seu espaço amostral por meio do produto externo
$$ \text{S}\times\ldots\times\text{S}=\left\{ \left(s_{1},\cdots,\,s_{n}\left|s_{i}\in S\right.\right)\right\}.$$
Definição: Dois eventos \(A\) e \(B\) são mutuamente excludentes se não podem ocorrer simultaneamente. Neste caso \(A\cap B=\emptyset\).

Definição: Uma coleção de subconjuntos de \(S\), que denotaremos por \(\{A_i\}\), é uma cobertura de \(S\) se os subconjuntos são mutuamente disjuntos (\(A_{i}\cap A_{j}=\emptyset\) para \(i\neq j\)) sua união é o próprio \(S\) (\(\underset{i}{\cup}A_{i}=S\)). Desta forma cada elemento de \(S\) está contido em exatamente um dos subconjuntos \(A_{i}\).
Definição: A cada evento de \(S\) associado ao experimento \(\varepsilon\) associamos uma probabilidade de ocorrência \(P\left(A\right)\), um número real, satisfazendo
Se \(\{A_{i}\}\) é uma coleção de eventos disjuntos (\(A_i \cap A_j=\emptyset\) para \(i\neq j\)) então \(P\left(\cup A_{i}\right)=\sum P\left(A_{i}\right)\).
Teorema: \(P(\emptyset)=0\)
Demonstração: \(A=A\cup\emptyset\) portanto \(P(A)=P\left(A\cup\emptyset\right)=P\left(A\right)+P\left(\emptyset\right)\Rightarrow P\left(\emptyset\right)=0 \)
Teorema: \(P(\overline{A})=1-P(A)\)
Demonstração: \(S=A\cup\overline{A}\), uma união disjunta. \(P\left(S\right)=1=P\left(A\right)+P\left(\overline{A}\right)\ \).
 Esta última propriedade é muito interessante em alguns casos onde é mais fácil calcular \(P\left(\overline{A}\right)\), a probabilidade de não ocorrer o evento \(A\).
Esta última propriedade é muito interessante em alguns casos onde é mais fácil calcular \(P\left(\overline{A}\right)\), a probabilidade de não ocorrer o evento \(A\).
Teorema: \(P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right)\)

Demonstração: \(A\cup B=A\cup\left(B\cap\overline{A}\right)\) e \(B=\left(B\cap A\right)\cup\left(B\cap\overline{A}\right)\). Como ambas uniões são disjuntas temos que
$$ P\left(A\cup B\right)=P\left(A\right)+P\left(B\cap\overline{A}\right)\,\,\,\text{e}\,\,\,P\left(B\right)=P\left(A\cap B\right)+P\left(\overline{A}\cap B\right) $$
$$ \Rightarrow P\left(A\cup B\right)=P\left(A\right)+P\left(B\right)-P\left(A\cap B\right).\ $$
Aplicando-se este mesmo resultado 2 vezes temos
$$
\begin{array}{rl}
P(A\cup B\cup C)= & P(A)+P(B)+P(C) \\
& -P(A\cap B)-P(B\cap C)-P(C\cap A)+P(A\cap B\cap C)
\end{array}
$$

Teorema: Se \(A\subset B\Longrightarrow P\left(A\right)\leq P\left(B\right)\)
Demonstração: Escreva \(B=A\cup\left(B\cap\overline{A}\right)\Longrightarrow P(B)=P(A)+P(B\cap\overline{A})\Longrightarrow P\left(A\right)\leq P\left(B\right).\)
Definição: Uma coleção de eventos \(\{A_i\}\) é uma partição de \(S\) se
Portanto, uma partição é uma coleção de subconjuntos de \(S\) mutuamente disjuntos, que cobrem todo o conjunto \(S\). Uma partição é uma cobertura composta de subconjuntos de probabilidade não nula. Devido à propriedade 1, quando um experimento é realizado apenas um dos eventos de uma partição ocorre de cada vez.
Vamos considerar, nesta seção, experimentos cujos resultados são descritos por um espaço amostral consistindo de um número finito de \(k\) elementos, \(S={ a_1,\ldots,\,a_k}\). Chamaremos de um evento simples (ou elementar) a um evento formado por um resultado simples, \(A={a_i} \). A cada evento simples associaremos uma probabilidade \(p_i=P({a_i})\) satisfazendo
Notamos que \(\left\{ a_{i}\right\} \cap\left\{ a_{j}\right\} =\emptyset,\;i\neq j,\) o que significa que a coleção de todos os eventos simples de \(S\) é uma partição do espaço amostral.
Se tomarmos um evento constituído de \(r\) destes eventos simples (\(1\leq r\leq k)\; A={a’_1,\ldots,\,a’_r}\) (uma combinação de \(r\) eventos quaisquer de S) então
$$ P\left(A\right)=p_{1}+p_{2}+\ldots+p_{r}=\sum^{r}p{}_{i.} $$
Isto significa que conhecemos a probabilidade de \(A\) se conhecermos a probabilidade dos elementos simples que a compõem.
Se todos os \(k\) resultados são igualmente verossímeis (ocorrem com a mesma probabilidade) então
$$ p_{i}=\frac{1}{k}\;\;\text{e}\;\;P(A)=\frac{r}{k}. $$
 Resumindo, se \(A\) é formado por \(k\) resultados simples igualmente prováveis então
Resumindo, se \(A\) é formado por \(k\) resultados simples igualmente prováveis então
$$ P(A)=\frac{\text{número de casos favoráveis}.}{\text{número de casos possíveis}} $$
Exemplo 2: Atirando uma moeda 2 vezes (ou duas moedas, ao mesmo tempo) qual é a probabilidade de se obter 1 cara? O experimento consiste em contar o número de caras resultantes e o espaço amostral é \(S={0,1,2}\). O evento favorável é \(A={1 \text{ cara }}={1 h}\). Note que \(P(A)\neq\frac{1}{3}\) pois os eventos de \(S\) não são igualmente verossímeis. Uma descrição mais apropriada do espaço amostral seria:
$$
S’=\{(h,h),\,(h,t),\,(t,h),\,(t,t)\}
$$
 O espaço amostral \(S’\) consiste de 4 casos possíveis, dois deles favoráveis. Portanto
O espaço amostral \(S’\) consiste de 4 casos possíveis, dois deles favoráveis. Portanto
$$ P(A)=P(1\text{cara})=\frac{2}{4}=0,5. $$
Isto mostra a importância de se conhecer técnicas de contagens de eventos.
Exemplo 3: Um dado honesto (bem balanceado) cai com qualquer das faces virada para cima com a mesma probabilidade. Jogando-se o dado uma vez, qual a probabilidade de que ele caia com um número maior que 2? O espaço amostral é \(S=\{1,2,3,4,5,6\}\), o evento favorável é \(A=\{3,4,5,6\}\). A probabilidade procurada é \(P(A)=4/6=2/3.\)
Exemplo 4: Jogando-se um dado 2 vezes, qual é a probabilidade de que a soma dos números obtidos seja 6?
Neste caso o espaço amostral é
$$ S=\left\{\begin{array}{cccc}
(1,1) & (1,2) & \ldots & (1,6) \\
\vdots & & & \vdots \\
(6,1) & (6,2) & \ldots & (6,6)
\end{array}\right\}.
$$
Destes eventos simples os únicos favoráveis são \(A=\{(1,5),\,(2,4),\,(3,3),\,(4,2),\,(5,1)\}.\) Portanto \(P(A)=5/36.\)
Vemos que é importante saber contar quantos eventos podem resultar de um certo experimento. Consideremos então a questão: de quantas maneiras diferentes podemos dispor de \(n\) objetos (permutações)? O primeiro pode ser escolhido entre \(n\) objetos, o segundo entre \(n-1\), até o útimo objeto restante. Como ilustrado na figura, o número resultante é \(n \times (n-1) \times \cdots \times 1 =n!\).
Como notação escreveremos \(_{n}P_{n}=n!\) para indicar a permutaçao de \(n\) objetos.
De quantas formas diferentes podemos escolher apenas \(r,\;(r\lt n)\) entre \(n\) objetos diferentes? Agora a escolha é interrompida após a seleção do \(r\)-ésimo objeto. Denotando por \(_{n}A_{r}\) este número temos
$$ _{n}A_{r}=n\left(n-1\right)\cdots\left(n-r+1\right)=\frac{n!}{\left(n-r\right)!}.$$
Se a ordem em que estes \(r\) elementos entram na seleção não é relevante então temos que remover da contagem acima as seleções repetidas. Temos que \(r\) objetos podem ser permutados de \(r!\) formas diferentes. Então, denotando por \(C\) o número de modos de permutar \(r\) entre \(n\) elementos, temos
$$ C=\frac{_{n}A_{r}}{r!}=\frac{n!}{r!\left(n-r\right)!}. $$
O número de combinações de \(n\) elementos em grupos de \(r\) elementos, sem que a ordem seja importante, aparece em diversas aplicações da matemática e recebe uma notação especial:
$$ C=\left(\begin{array}{c} n \\ r \end{array}\right)=\frac{n!}{r!\left(n-r\right)!}. $$
Estes são os chamados coeficientes binomiais. Eles possuem diversas propriedades interessantes. Entre elas, se \(n\) é um inteiro positivo e \(0\leq r\leq n\) então
$$
\left( \begin{array}{c} n \\ r \end{array}\right) =
\left(\begin{array}{c} n \\ n-r \end{array}\right), \;\;\;\;
\left(\begin{array}{c} n \\ r \end{array}\right)=
\left(\begin{array}{c} n-1 \\ r-1 \end{array}\right) +
\left(\begin{array}{c} n-1 \\ r \end{array}\right)
$$
Exemplo 5:. Na Loteria brasileira Megasena uma aposta simples consiste em escolher 6 entre 60 números. Qual a probabilidade de se escolher os 6 números sorteados? Temos que
$$ C=\left(\begin{array}{c} 60 \\ 6 \end{array}\right)=\frac{60!}{6!(54)!}=50063860 $$
é o número de resultados possíveis. A probabilidade de se acertar com um jogo simples é \(1/50063860\).
Observe que a operação acima pode ser simplificada da seguinte forma:
$$ \frac{60!}{6!(54)!}=\frac{55\times56\times57\times58\times59\times60}{2\times3\times4\times5\times6}=50063860. $$
(Os primeiros \(54\) fatores no numerador são cancelados por \(54!\) no denominador.)
Vamos usar de um exemplo para mostrar a diferença entre escolher objetos de um lote inicial, fazendo ou não a reposição dos objetos retirados após cada escolha.
Exemplo 6: Em um lote com 100 peças, 20 são defeituosas. Retiramos 2 peças e definimos dois eventos: \(\;A=\){1ª peça com defeito} \(B=\){2ª peça com defeito}. Se há reposição da peça retirada temos:
$$P(A)=\frac{20}{100}=\frac{1}{5},\;\;\; P(B)=\frac{1}{5}.$$
Mas, se não há a reposição, após a retirada da primeira peça restam 99, mas não sabemos quantas são defeituosas. Vamos denotar por \(P(B|A)\) = a probabilidade condicionada do evento \(B,\) tendo ocorrido o evento \(A.\) Se a primeira peça tinha defeito, restam 19 peças com defeito em um lote de 99, e \(P(B|A)=\frac{19}{99}\).
Como \(A\) ocorreu, o espaço amostral fica reduzido. Observe ainda que a probabilidade de \(B\) se \(A\) não tiver ocorrido é \(P(B|\overline{A})=\frac{20}{99}\).

Exemplo 7: Ex.: Dois dados são lançados e representamos o resultado por \(\left(x_{1},\,x_{2}\right).\) O espaço amostral é
$$
S=\left\{ \begin{array}{cccc}
(1,1) & (1,2) & \ldots & (1,6) \\
(2,1) & (2,2) & \ldots & (2,6) \\
\vdots & & & \vdots \\
(6,1) & (6,2) & \ldots & (6,6)
\end{array}\right\},
$$
consistindo de 36 eventos simples. Considere 2 eventos: \(A\) onde a soma dos dados é 10; \(B\) onde o primeiro resultado é maior que o segundo:
$$
\begin{array}{rl}
A= & \{(x_1,x_2)|x_1 + x_2=10\} = \{(4,6),(5,5),(6,4)\} \\ & \\
B= & \left\{(x_1,x_2)|x_1 \gt x_2\right\} \\
= & \left\{(2,1),(3,1),(3,2),(4,1),(4,2),(4,3),(5,1),\right. \\
& \left.(5,2),(5,3),(5,4),(6,1),(6,2),(6,3),(6,4),(6,5)\right\}
\end{array}
$$
A probabilidade de ocorrerem \(A\) e \(B\) são, respectivamente,
$$ P\left(A\right)=\frac{3}{6},\;\;P(B)=\frac{15}{36},$$
enquanto a probabilidade condicionada de ocorrer \(B\) tendo ocorrida \(A\) é $$ P(B|A)=\frac{1}{3}. $$ O espaço amostral se reduz para \(A={(4,6),\,(5,5),\,(6,4)}\) e, entre estes eventos apenas \((6,4)\) é favorável. Da mesma forma a probabilidade de ocorrer \(A\) tendo ocorrido \(B\) é
$$ P(A|B)=\frac{1}{15}, $$
pois \(\text{ord}(B)=15\) e apenas o evento \(\left(6,4\right)\) é favorável. Observe ainda que a probabilidade de que \(A\) e \(B\) ocorram simultaneamente é
$$ P(A\cap B)=\frac{1}{36}.$$
 Note que:
Note que:
$$P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{1}{36}\frac{36}{15}=\frac{1}{15}$$
$$P(B|A)=\frac{P(B\cap A)}{P(A)}=\frac{1}{36}\frac{36}{3}=\frac{1}{3}$$
Isto sugere a definição de probabilidade condicionada (que pode ser formalmente demostrada):
$$ P(B|A)=\frac{P(A\cap B)}{P(A)} $$
para \(P(A)\gt 0\). É claro que, se \(P(A)=0\), \(P(B|A)=0\). Podemos então escrever
$$ P(A\cap B)=P(B|A)P(A)=P(A|B)P(B). $$

Exemplo 8: Entre 100 calculadoras temos aparelhos novos (N) e usados (U), eletrônicos (E) e manuais (M), de acordo com a tabela:

Uma é escolhida ao acaso e verifica-se que é nova. Qual probabilidade de que ela seja eletrônica?
Como já se vericou que a calculadora é nova, o espaço amostral fica reduzido à apenas 70 unidades. Nele apenas 40 calculadoras são eletrônicas. Usando a definição de probabilidade condicionada temos
$$ P(E|N)=\frac{P(E\cap N)}{P(N)}=\frac{40/100}{70/100}=\frac{4}{7}.$$
Exemplo 9: Retomamos a situação das 100 peças, sendo 20 com defeito. Qual a probabilidade de se escolher 2, sem reposição, e serem ambas defeituosas?
Definimos os eventos A = {1ª com defeito}; B = {2ª com defeito}. O evento favorável é \(A\cap B\) e sua probabilidade é
$$ P(A\cap B)=P(B|A)P(A)=\frac{19}{99}\frac{20}{100}=\frac{19}{495}. $$
Uma observação será útil antes de prosseguirmos: seja \(\{M_{i}\}\) \(i=1,\ldots,\,k,\) é uma partição de \(S\). Podemos decompor \(B\) em partes mutuamente excludentes

$$ A=(A\cap M_{1})\cup\cdots\cup(A\cap M_{k}). $$
Portanto:
$$ P(A)=\sum_{i}P(A\cap M_{i})=\sum_{i}P(A|M_{i})P(M_{i}). $$
Exemplo 10: Na mesma situação anterior, qual a probabilidade de, escolhendo 2 peças, a segunda ter defeito? Novamente temos \(A=\) {1ª com defeito}; \(B=\) {2ª com defeito}. Queremos calcular \(P(B)\). Podemos escrever \(B\) como a união disjunta \(B=\left(B\cap A\right)\cup\left(B\cap\bar{A}\right)\). Então
$$
\begin{array}{rl}
P(B)= & P\left(B\cap A\right)+P\left(B\cap\bar{A}\right)=P(B|A)P(A)+P(B|\bar{A})P(\bar{A}) \\
= & \frac{19}{99}\frac{1}{5}+\frac{20}{99}\frac{4}{5}=\frac{1}{5}.
\end{array}
$$
Exemplo 11: Um produto é manufaturado por 3 fábricas diferentes que chamaremos de \(F_{1},\,F_{2}\)e \(F_{3}\). A quantidade de peças produzida por cada fábrica e a porcentagem de defeitos são exibidas na tabela:
| Fábrica | produção/dia | peças com defeito |
| F1 | 2 | 2% |
| F2 | 1 | 2% |
| F3 | 1 | 4% |
Após um certo tempo a produção das 3 fábricas é colocada em um depósito e uma peça é retirada ao acaso. Qual é a probabilidade dela ser defeituosa? Vamos definir os seguintes eventos \(D=\) {peça com defeito}; \(F_i\) = {peça fabricada por \(F_i\)}, \(i=1,2,3\). Podemos usar a união disjunta \(D=\cup_{i}(D\cap F_{i})\) para calcular
$$
\begin{array}{rl}
P(A)=& \sum_{i}P(D\cap F_{i})=\sum_{i}P(D|F_{i})P(F_{i})\\
=& P(D|F_{1})P(F_{1})+P(D|F_{2})P(F_{2})+P(D|F_{3})P(F_{3}) \\
=& 00,2\frac{1}{2}+00,2\frac{1}{4}+00,4\frac{1}{4}=0,025.
\end{array}
$$
Podemos ainda fazer a seguinte pergunta: Suponha que a peça retirada é defeituosa. Qual é a probabilidade de que ela tenha sido produzida na \(F_1?\) Queremos, portanto, \(P(F_{1}|D)\). Usamos
$$
\begin{array}{rl}
P(F_1|D)= & \frac{P(D|F_1)P(F_1)}{P(D)}=\frac{P(D|F_1)P(F_{1})}{\sum_{i=1}^{3}P(D|F_i)P(F_i)}= \\
& \frac{(0,02)\frac{1}{2}}{(0,02)\frac{1}{2}+(0,02)\frac{1}{4}+(0,04)\frac{1}{4}}=0,04,
\end{array}
$$
onde, na segunda igualdade, foi usado o fato de que \({F_i}\) é uma partição do espaço amostral.

Seja \({B_i}\) uma partição do espaço amostral e \(A\) um evento de \(S.\) Então
$$ P(B_i|A)=\frac{P(A|B_i)\,P(B_i)}{\sum_{k=1}^{3}P(A|B_k)\,P(B_k)},\:i=1,…,\,n. $$
Dois eventos são ditos independentes se a ocorrência de um não afeta a probabilidade de ocorrência do outro.
Exemplo 12: Um dado é jogado 2 vezes. Definimos os eventos \(A=\){1º mostra número par}, \(B=\){2º cai 5 ou 6}. Vemos que são dois eventos não relacionados. Temos
$$ P(A)=\frac{1}{2},\;\; P(B)=\frac{1}{3}.$$
$$ P(A\cap B)=\frac{6}{36}=\frac{1}{6}, $$
pois \(A\cap B=\{(2,5),(2,6),(4,5),(4,6),(6,5),(6,6)\}\). Consequentemente
$$ P(A|B)=\frac{P(A\cap B)}{P(B)}=\frac{1}{2}. $$
Observamos que \(P(A|B)=P(A).\) Da mesma forma \(P(B|A)=P(B).\)
Definição: \(A\)e \(B\)são eventos independentes se, e somente se, \(P(A\cap B)=P(A)P(B).\)
Como vimos a analiticidade de uma função complexa é uma característica bastante restritiva. é possível que uma função seja analítica em uma região e não seja em outra, ou que deixe de ser analítica apenas em um número finito de pontos de seu domínio.
Definição: Se uma função \(f\) é analítica em uma região \(R\), exceto em um subconjunto \(S\) de \(R\) então os pontos de \(S\) são chamandos de pontos singulares desta função ou, simplesmente, singularidades. Como exemplo, \(z_0=0\) é singularidade de \(1/z\) e \(1/z^{2}\), enquanto \(z_0=\pm i\) são as singularidares de \(1/(z^{2}+1)\). Por outro lado a função \(f(z) =\left\vert z\right\vert^{2}\) não tem nenhum ponto singular já que não é analítica em nenhum ponto de seu domínio. As séries de Laurent representam o instrumento adequado para o estudo das sigularidades de uma função.
Se \(f\) é analítica em alguma vizinhança de um ponto \(z_0\), exceto no próprio ponto \(z_0\), então dizemos que \(z_0\) é uma singularidade isolada da função \(f\). Como exemplo temos que a função
$$
f(z) =\frac{1}{1-\cos z}
$$
é singular nos pontos \(z=2n\pi,\;\;n=0,\pm 1,\ \pm 2,\cdots\), que são os pontos onde o denominador se anula. Se \(z_0\) é uma singularidade isolada de uma função \(f\) então ela admite o desenvolvimento de Laurent
$$
f(z)=\sum\limits_{n=1}^{\infty}\frac{a_{-n}}{(z-z_0)^{n}}+\sum\limits_{n=0}^{\infty}a_{n}(z-z_0)^{n}=\sum\limits_{n=-\infty }^{\infty }a_{n}(z-z_0)^{n},
$$
válido na região \(0\lt \left\vert z-z_0\right\vert \lt r,\;\) a chamada vizinhança perfurada de \(z_0\). Os coeficientes da expansão são, como já vimos,
$$
a_{n}=\frac{1}{2\pi i}\oint\limits_{C}\frac{f(z) dz}{(z-z_0)^{n+1}},
$$
onde \(C\) é um contorno fechado que envolve \(z_0\) uma vez, no sentido positivo. Em particular estaremos interessados em obter o coeficiente \(a_{-1}\), definido abaixo, por um motivo que logo ficará claro.
Definição: Ao coeficiente \(a_{-1}\) da expansão de Laurent para uma função \(f\) analítica em uma vizinhança perfurada de \(z_0\) chamamos de resíduo de \(f\) no ponto singular isolado \(z_0\) e denotamos
$$
\text{Res}( f,z_0) =a_{-1}=\frac{1}{2\pi i}\oint\limits_{C}f(z) dz.
$$
A expressão acima fornece uma forma para o cálculo de uma integral de contorno com integrando complexo. Para isto basta encontrar a expansão de Laurent em séries para o integrando e identificar o resíduo da função em seu ponto singular Embora pela equação (2) acima já sabemos que \(\oint\nolimits_{C}f(z) dz=2\pi i\text{Res}( f,z_0)\), pode ser esclarecedor, apesar de repetitivo, mostrar o seguinte procedimento. Se \(z_0\) é ponto singular isolado de \(f\) então esta função admite a série de Laurent
$$
f(z) =\sum\limits_{n=-\infty }^{\infty }a_{n}(z-z_0)^{n}.
$$
Dentro da região de convergência da série ela pode ser integrada termo a termo,
$$
I=\oint\limits_{C}f(z) dz=\sum\limits_{n=-\infty }^{\infty}a_{n}\oint\limits_{C}(z-z_0)^{n}dz.
$$
Fazendo \(z-z_0=\delta e^{i\theta }\) temos \(dz=i\delta e^{i\theta }d\theta\) e, caso \(n\neq -1\),
$$
\oint\limits_{C}(z-z_0)^{n}dz=i\delta^{n+1}\int_0^{2\pi}e^{i\theta ( n+1)}d\theta =i\delta^{n+1}\left. \frac{e^{i\theta ( n+1)}}{i( n+1)}\right\vert _0^{2\pi }=\frac{\delta^{n+1}}{n+1}\left[ e^{2( n+1) i\pi }-1\right] =0.
$$
O único termo não nulo ocorre para \(n=-1\),
$$
\oint\limits_{C}\frac{dz}{z-z_0}=2\pi i.
$$
Como já afirmado, a integral avaliada em (3) é
$$
\oint\limits_{C}f(z) dz=2\pi i\ a_{-1}.
$$
O uso do cálculo de resíduos para calcular integrais sobre contornos fechados de uma função que envolve pontos singulares isolados é exemplificado a seguir.
Exemplo 1: Podemos calcular a integral
$$
I=\oint\limits_{\left\vert z\right\vert =2}e^{-z}(z-1)^{-2}dz
$$
simplesmente encontrando o resíduo do integrando. A única singularidade deste integrando é \(z_0=1\), um ponto que está na região interior ao contorno de integração. Devemos então encontrar a série de Laurent para o integrando. Para isto observe que
$$
e^{-z}=e^{-z+1-1}=e^{-1}e^{-(z-1)
}=e^{-1}\sum\limits_{n=0}^{\infty }\frac{(-1)^{n}}{n!}(
z-1)^{n},
$$
e, portanto,
$$
f=\frac{e^{-z}}{(z-1)^{2}}=\frac{e^{-z}}{(z-1)^{2}}\left[ 1-(z-1) +\frac{(z-1)^{2}}{2!}-\frac{(z-1)^{3}}{3!}+\ldots \right],
$$
$$
=\frac{e^{-z}}{(z-1)^{2}}\left[ \frac{1}{(z-1)^{2}}-\frac{1}{(z-1)}+\frac{1}{2!}-\frac{(z-1)}{3!}+\ldots \right]
$$
de onde ser observa que \(a_{-1}=\text{Res}( f,1) =-e^{-1.}\) Portanto temos que
$$
\oint\limits_{\left\vert z\right\vert =2}e^{-z}(z-1)^{-2}dz=2\pi i\text{Res}( f,1) =-\frac{2\pi i}{e}.
$$
Exemplo 2: Para calcular \(\oint\nolimits_{\left\vert z\right\vert =1}\exp ( 1/z^{2}) dz\) observamos que a única singularidade do integrando é \(z=0\), um ponto interior ao contorno de integração. Observe que, fazendo \(u=1/z^{2}\) temos
$$
e^{u}=\sum\limits_{n=0}^{\infty }\frac{u^{n}}{n!}=\sum\limits_{n=0}^{\infty }\frac{1}{n!}\frac{1}{z^{2n}}=1+\frac{1}{z^{2}}+\frac{1}{2!z^{4}}+\frac{1}{3!z^{6}}+\ldots ,
$$
convergente em \(\left\vert z\right\vert \gt 0\). O resíduo é \(\text{Res}( f,0) =0\) e
$$
\oint\limits_{\left\vert z\right\vert =1}\exp ( 1/z^{2}) dz=2\pi i\text{Res}( f,0) =0.
$$
Enunciamos a seguir o teorema dos resíduos, útil para o cálculo de integrais realizada sobre um caminho que circula um número finito de singularidades. Observamos que, se uma função possui um número finito de pontos singulares em um domínio então estes pontos são necessariamente isolados.
Teorema: Seja \(f\) uma função analítica sobre o contorno fechado \(C\) e em seus pontos interiores, exceto em um número finito de pontos, \(z_{1},\ z_{2},\ldots ,\ z_{n}\), interiores a \(C\). Então
$$
\oint\limits_{C}f(z) dz=2\pi i\sum\limits_{k=1}^{n}\text{Res}( f,z_{k}) ,
$$
onde o contorno é percorrido uma vez, no sentido positivo e \(\text{Res}( f,z_{k})\) é o resíduo da função \(f\) no ponto \(z_{k}\).
Demonstração: Como os pontos singulares são isolados podemos construir círculos \(C_{k}\) com centro em \(z_{k}\) e raios suficientemente pequenos para que cada círculo envolva apenas a singularidade em seu centro. Em seguida construimos o caminho \(\gamma =C\cup (-C_{1}) \cup(-C_{2}) \cup \ldots \cup (-C_{k}),\) como mostrado na figura 1.

A função \(f\) é analítica em \(\gamma\) e seu interior de forma que
$$
0=\oint\limits_{\gamma }f(z) dz=\oint\limits_{C}f(
z) dz-\oint\limits_{C_{1}}f(z)
dz-\oint\limits_{C_{2}}f(z) dz-\ldots
-\oint\limits_{C_{n}}f(z) dz
$$
ou seja
$$
\oint\limits_{C}f(z)
dz=\sum\limits_{k=1}^{n}\oint\limits_{C_{1}}f(z) dz=2\pi
i\sum\limits_{k=1}^{n}\text{Res}( f,z_{k}).
$$
Exemplo 3: Para mostrar a utilidade do teorema acima vamos calcular
$$
\oint\limits_{\left\vert z\right\vert =2}\frac{5z-2}{z(z-1)}dz.
$$
Observamos, inicialmente, que os pontos sigulares do integrando são \(z=0\) e \(z=1\), ambos interiores à região circundada por \(C\). Devemos determinar os resíduos do integrando nestes pontos. Em torno de \(z=0\) a função \(1/( 1-z)\) é analítica e tem série de Taylor dada por
$$
\frac{1}{z-1}=-\sum\limits_{n=0}^{\infty }z^{n},\ \left\vert z\right\vert \lt 1.
$$
O integrando pode ser escrito como
$$
\frac{5z-2}{z}\frac{1}{z-1}=\frac{2-5z}{z}\sum\limits_{n=0}^{\infty}z^{n}=( \frac{2}{z}-5) \sum\limits_{n=0}^{\infty }z^{n}=
$$
$$
=2\sum\limits_{n=0}^{\infty }z^{n-1}-5\sum\limits_{n=0}^{\infty }z^{n}=\frac{2}{z}-3\sum\limits_{n=0}^{\infty }z^{n},
$$
válida em \(0\lt \left\vert z\right\vert \lt 1\). Concluímos que \(\text{Res}( f,0) =2\).
Por outro lado, na vizinhança de \(z=1\) temos que \(1/z\) é a função analítica. Queremos escrever o integrando em potências de \((z-1)\) para descobrir qual é o seu resíduo neste ponto. Fazemos
$$
\frac{1}{z}=\frac{1}{z-1+1}=\sum\limits_{n=0}^{\infty }(-1)^{n}(z-1)^{n},\;\; \left\vert z-1 \right\vert \lt 1,
$$
e, portanto,
$$
\frac{5z-2}{z(z-1)}=( \frac{5z-5+3}{z-1}) \frac{1}{z}=( 5+\frac{3}{z-1}) \sum\limits_{n=0}^{\infty }(-1)^{n}(z-1)^{n}=
$$
$$
=5\sum\limits_{n=0}^{\infty }(-1)^{n}(z-1)
^{n}+3\sum\limits_{n=0}^{\infty }(-1)^{n}(z-1)
^{n-1}=\frac{3}{z-1}+2\sum\limits_{n=0}^{\infty }(-1)
^{n}(z-1)^{n}.
$$
Na última igualdade foi feito:
$$
3\sum\limits_{n=0}^{\infty }(-1)^{n}(z-1)^{n-1}=\frac{3}{z-1}+3\sum\limits_{n=1}^{\infty }(-1)^{n}(
z-1)^{n-1}=\frac{3}{z-1}+3\sum\limits_{n=0}^{\infty }(
-1)^{n+1}(z-1)^{n}.
$$
O resíduo neste ponto é \(\text{Res}( f,1) =3\) e
$$
\oint\limits_{\left\vert z\right\vert =2}\frac{5z-2}{z(z-1)}dz=2\pi i\left[ \text{Res}( f,0) +\text{Res}(
f,1) \right] =10\pi i.
$$
Observe que, neste caso, seria mais fácil escrever o integrando usando frações parciais,
$$
\frac{5z-2}{z(z-1)}=\frac{2}{z}+\frac{3}{z-1}
$$
e, portanto,
$$
\oint\limits_{\left\vert z\right\vert =2}\frac{5z-2}{z(z-1)}dz=2\oint\limits_{\left\vert z\right\vert =2}\frac{dz}{z}+3\oint\limits_{\left\vert z\right\vert =2}\frac{dz}{z-1}=10\pi i.
$$
Nem sempre é possível, no entanto, proceder desta última forma e, frequentemente a integração pelo método dos resíduos representa uma ferramenta poderosa para a solução de integrais definidas, como veremos.
Se a série de Laurent de uma função
$$
\begin{array}{ccc}
f(z)=& \underbrace{\sum\limits_{n=1}^{\infty }\frac{a_{-n}}{(z-z_0)^{n}}} & +\underbrace{\sum\limits_{n=0}^{\infty}a_{n}(z-z_0)^{n}}, \\
& \text{ parte principal} & \text{ parte analítica}
\end{array}
$$
é composta por um número finito de termos na parte principal então existe um maior inteiro \(m\) tal que \(a_{-m}\) seja não nulo e
$$
f(z)=\frac{a_{-1}}{z-z_0}+\frac{a_{-2}}{(z-z_0)^{2}}+\ldots +\frac{a_{-m}}{(z-z_0)^{m}}+\sum\limits_{n=0}^{\infty }a_{n}(z-z_0)^{n}.
$$
Neste caso \(z_0\) é dito um pólo de ordem \(m\). Se \(m=1\) então o pólo é simples. Se a parte principal tem infinitos termos o pólo é dito essencial.
Exemplo 4: A função
$$
f(z) =\frac{z^{2}+1}{z-1}
$$
tem um pólo simples em \(z=1\). Para confirmar isto fazemos
$$
f(z) =\frac{(z-1)^{2}+2z}{z-1}=(z-1) +\frac{2z-2+2}{z-1}=(z-1) +2+\frac{2}{z-1}.
$$
Além disto \(\text{Res}( f,~1) =2\).
Exemplo 5: A função
$$
f(z) =\frac{z^{2}-2z+3}{z-2}
$$
pode ser escrita como
$$
f(z) =\frac{(z-2)^{2}+2z-1}{z-2}=(z-2) +\frac{2z-4+3}{z-2}=(z-2) +2+\frac{3}{z-2}.
$$
Então \(z=2\) é um pólo simples e \(\text{Res}( f,~2)=3\).
Exemplo 6: A seguinte função tem um pólo em \(z=0\) de ordem 3 e \(\text{Res}( f,0) =0:\)
$$
f(z) =\frac{\text{ senh }z}{z^{4}}=\frac{1}{z^{4}}(z+\frac{z^{3}}{3!}+\frac{z^{5}}{5!}+\frac{z^{7}}{7!}+\ldots ) =\frac{1}{z^{3}}+\frac{1}{3!}+\frac{z}{5!}+\frac{z^{3}}{7!}+\ldots .
$$
Já o \(\cosh ( 1/z)\) tem uma singularidade essencial em \(z=0\) e resíduo nulo:
$$
\cosh \left( \frac{1}{z} \right) =\sum\limits_{n=0}^{\infty }\frac{1}{(2n) !}\frac{1}{z^{2n}}.
$$
Recordamos que
$$
\cosh z=\frac{1}{2}( e^{z}+e^{-z}) =\frac{1}{2}(
\sum\limits_{n=0}^{\infty }\frac{z^{n}}{n!}+\sum\limits_{n=0}^{\infty
}(-1)^{n}\frac{z^{n}}{n!}) =
$$
$$
=\sum\limits_{n=\text{par}}^{\infty }\frac{z^{n}}{n!}=\sum\limits_{n=0}^{\infty }\frac{z^{2n}}{( 2n) !}.
$$
Suponha que \(f\) tem um pólo de ordem \(m\) em \(z_0\). Neste caso a função
$$
\phi (z) =(z-z_0)^{m}f(z) ,
$$
definida em \(0 \lt |z-z_0|\lt r_{1}\) é uma função analítica definida em uma vizinhança de \(z_0\), exceto no próprio \(z_0\), uma vez que \(f\) não é definida neste ponto. Devido à expressão de Laurent para \(f\), dada em (4) podemos escrever
$$
\phi (z) =a_{-1}(z-z_0)^{m-1}+a_{-2}(z-z_0)^{m-2}+\ldots +a_{-m}+\sum\limits_{n=0}^{\infty }a_{n}(z-z_0)^{m+n},
$$
onde \(a_{-m}\neq 0\). Se definirmos esta função no ponto \(z_0\) como \(\phi (z_0) =a_{-m}\) então a representação em (5), sendo convergente, é válida na vizinhança de \(z_0\) incluindo o próprio ponto \(z_0\), definindo uma função analítica \(\phi\). A definição de \(\phi (z_0)\) dada acima é equivalente à
$$
\phi (z_0) =\lim_{z\rightarrow z_0}(z-z_0)^{m}f(z) =a_{-m}.
$$
Como \(a_{-m}\) é finito e não nulo concluímos que \(|f(z) |\) deve necessariamente tender a infinito quando \(z\rightarrow z_0\).
Um outro tipo de singularidade é a denominada ponto singular removível: se uma função \(\phi\) pode se tornada analítica em seu ponto singular \(z_0\) simplesmente por meio da atribuição de um valor conveniente para \(\phi (z_0)\) então dizemos que \(z_0\) é um ponto singular removível de \(\phi\). Um exemplo disto é a função \(\phi (z) =(z-z_0)^{m}f(z)\), definida à partir de \(f\), uma função com pólo de ordem \(m\) em \(z_0\). Observe que esta função tem representação em séries de Taylor dada por (5), de forma que
$$
a_{-1}=\frac{\phi^{( m-1)}(z_0)}{(m-1)!}.
$$
Em particular, quando o pólo é simples, \(m=1\) e \(a_{-1}\) é o resíduo da função \(f\) no ponto \(z_0\) temos que
$$
a_{-1}=\phi (z_0) =\lim_{z\rightarrow z_0}(z-z_0) f(z).
$$
Por outro lado, se uma função \(f\) é tal que o produto
$$
(z-z_0)^{m}f(z) =\phi (z)
$$
possa ser definido em \(z_0\) de modo a ser analítico neste ponto podemos encontrar a representação de Taylor
$$
(z-z_0)^{m}f(z) =\phi (z)
=\sum\limits_{n=0}^{\infty }\frac{\phi^{( n)}(z_0)}{n!}(z-z_0)^{n}.
$$
Um uma vizinhança de \(z_0\), para pontos distintos de \(z_0\) temos
$$
f(z) =\frac{\phi (z)}{(z-z_0)^{m}}=\sum\limits_{n=0}^{\infty }\frac{\phi^{( n)}(z_0)}{n!}(z-z_0)^{n-m}=\sum\limits_{n=-m}^{\infty }\frac{\phi^{(n+m)}(z_0)}{( n+m) !}(z-z_0)^{n}.
$$
Concluimos dai que \(f\) tem um pólo de ordem \(m\) em \(z=z_0\) e que seu resíduo é dado pela fórmula (6). Estas considerações implicam em um teste para a existências de pólos, descrito no teorema que se segue.
Teorema: Se \(f\) uma função singular no ponto \(z_0\) mas, para algum inteiro \(m\) a função
$$
\phi (z) =(z-z_0)^{m}f(z) ,\;\; \phi (z_0) \neq 0,
$$
é analítica em \(z_0\) então \(z_0\) é pólo de ordem \(m\) de \(f\) e
$$
\text{Res}(f,~z_0) =\left\{
\begin{array}{ll}
\phi (z_0) =\lim_{z\rightarrow z_0}(z-z_0)f(z) ,\; & \text{ se }\; m=1, \\
\frac{\phi^{(m-1)}(z_0)}{(m-1)!}, & \text{se }\; m \gt 1.
\end{array}
\right.
$$
Note que, em particular, as condições do teorema são satisfeitas se
$$
f(z) =\frac{\phi (z)}{(z-z_0)^{m}},\;\;m=1,2,\ldots ,
$$
e a função \(\phi\) é analítica em \(z_0\), com \(\phi (z_0)\) não nulo.
Exemplo 7: A função
$$
f(z) =\frac{\exp ( -2z)}{z^{3}}
$$
satisfaz às condições do teorema. Ela tem um ponto singular em \(z_0=0\), e
$$
\phi (z) =\exp ( -2z)
$$
é analítica e não nula em \(z=0\). Como \(m=3\) seu resíduo neste ponto, de acordo com a fórmula (7), é
$$
\text{Res}( f,\ 0) =\frac{\phi^{( 2)}(0)}{2!}=2.
$$
Exercícios :
1. Encontre os pólos, suas ordens e os resíduos das funções para cada pólo:
$$
\begin{array}{lll}
\text{ a. }\;\; \frac{z+4}{z(z^{2}+1)} & \text{ b. }\;\;
\frac{\text{sen }z}{z^{3}(z-\pi )} & \text{ c. }\;\;\frac{1}{z\text{sen }^{2}\pi z} \\
\text{ d. }\;\;\frac{1-e^{z}}{z^{4}\text{sen }( 1+z)} &
\text{ e. }\;\;\frac{e^{z}}{z( 1-e^{-z})} & \text{ f. }\;\;\frac{1}{(e^{iz}-1)^{2}}\; \\
\text{ g. }\;\;\frac{\cosh z}{z( 1-\cos z)} & \text{ h. }\;\;\frac{\text{ senh }z}{z\text{sen }^{2}(z+\pi /2)}
\end{array}
$$
2. Mostre que \(z=0\) é singularidade removível em cada uma das funções abaixo. Determine o valor a se atribuir em \(z=0\) para que as funções sejam analíticas.
$$
\begin{array}{lll}
\text{ a. }\;\; \frac{z}{e^{z}-1} & \text{ b. }\;\;\frac{e^{z}-1}{\text{sen }2z} & \text{ c. }\;\;\frac{\cosh 2z-1}{\text{sen }^{2}z} \\
\text{ d. }\;\;\frac{1}{e^{z}-1}-\frac{1}{z} & \text{ e. }\;\;\frac{1}{z}-\frac{1}{\text{sen }z} & \text{ f. }\;\;\frac{1}{(e^{iz}-1)^{2}} \\
\text{ g. }\;\;\frac{\cosh z}{z( 1-\cos z)} & \text{ h. }\;\;\frac{\text{ senh }z}{z\text{sen }^{2}(z+\pi /2)} &
\end{array}
$$
3. Encontre a parte principal da função \(f(z) =1/z(z-i)^{2}\) em relação ao pólo \(z=i\).
Algumas respostas e sugestões:
1a. \(z=0,\; i,\; -i,\;\) de ordens \(1,\, 2\) e \(2\) respectivamente.
1c. \(z=0\) de ordem 3, \(z=\pm 1,\pm 2, \pm 3, \ldots \) de ordem \(2\), cada.
1e. \(z=0\) de ordem 2, \(z=2k\pi , k\neq 0\) inteiro, de ordem 1, cada.
1g. \(z=0\) de ordem 3, \(z=2k\pi ,\; k\neq 0\;\) inteiro, de ordem 2, cada.
3. \(\frac{-i}{(z-i)^{2}}+\frac{1}{z-i}\)
Uma aplicação importante para o cálculo de integrais complexas usando a teoria dos resíduos está na avaliação de integrais impróprias com integrandos reais. Podemos desde já fornecer um exemplo deste uso.
Exemplo 8: Vamos usar o teorema dos resíduos para calcular a integral
$$
I=\int_{-\infty }^{\infty }\frac{dx}{x^{2}+1}.
$$
Embora esta seja uma integral real, efetuada sobre todo o eixo real, ela pode ser colocada como parte de uma integração no plano complexo, mais fácil de ser calculada. Para ver isto considere a integral
$$
\oint\limits_{C}\frac{dz}{z^{2}+1}
$$
onde \(C\) é o contorno \(C=C_{R}\cup L\), representado na figura 2. \(C_{R}\) é o arco de circunferência de raio \(R\) em \(y\gt 0\), enquanto \(L\) é o segmento de reta de \(-R\) até \(R\) sobre o eixo real.

O integrando é
$$
\frac{1}{z^{2}+1}=\frac{1}{z+i}\frac{1}{z-i}=\frac{1}{2i}\frac{1}{z-i}+\frac{1}{4}\sum ( \frac{i}{2})^{n}(z-i)^{n}
$$
que tem um pólo simples em \(z=i\), o único envolvido pelo contorno, e resíduo, neste ponto \(\text{Res}( f,i) =1/2i\). Alternativamente, usando a fórmula (7) temos que
$$
(z-i) \frac{1}{z^{2}+1}=\frac{1}{z+i}=\phi
$$
que é analítica em \(z=i\). Dai o pólo é simples e
$$
\text{Res}( \frac{1}{z^{2}+1},\ i) =\phi ( i) =\frac{1}{2i}.
$$
Dai concluimos que
$$
\oint\limits_{C}\frac{dz}{z^{2}+1}=\pi .
$$
Observamos que \(\oint\nolimits_{C}=\int_{I}+\int_{C_{R}}\), ou seja,
$$
\pi =\int_{-R}^{R}\frac{dx}{x^{2}+1}+\int_{C_{R}}\frac{dz}{z^{2}+1}.
$$
Resta apenas observar que, no limite \(R\rightarrow \infty\) a segunda integral é nula. Para ver isto note que sobre \(C_{R}\) temos que \(\left\vert z\right\vert =R\) e
$$
\left\vert z^{2}+1\right\vert \geq \left\vert z^{2}\right\vert -1=R^{2}-1,
$$
onde usamos a desigualdade
$$
\left\vert z_{1}+z_{2}\right\vert \geq \left\vert z_{1}\right\vert -\left\vert z_{2}\right\vert .
$$
Como consequência
$$
\left\vert \int_{C_{R}}\frac{dz}{z^{2}+1}\right\vert \leq \frac{1}{R^{2}-1}\int_{C_{R}}\left\vert dz\right\vert =\frac{\pi R}{R^{2}-1}\underset{R\rightarrow \infty }{\longrightarrow }0.
$$
Resta apenas a integral que queríamos calcular:
$$
\int_{-\infty }^{\infty }\frac{dx}{x^{2}+1}=\pi .
$$
O procedimento mostrado acima pode ser generalizado para o cálculo de integrais na forma de
$$
\int_{-\infty }^{\infty }\frac{P(x)}{Q(x)}dx
$$
onde \(P\) e \(Q\) são polinômios que diferem, em graus, da seguinte forma
$$
\text{grau }Q-\text{grau }P=m\geq 2.
$$
Como antes, tomamos as extensões das funções envolvidas, \(P(z)\) e \(Q(z)\) e construímos um contorno \(C=C_{R}\cup L\), idêntico ao da figura 2, usada no exemplo anterior. Como \(z^{m}P(z)\) e \(Q(z)\) têm o mesmo grau, o limite
$$
\lim_{z\rightarrow \infty }\frac{z^{m}P(z)}{Q(z)}=M
$$
é finito e não nulo. Em outras palavras, para \(|z|=R\) suficientemente grande temos que
$$
\left\vert \frac{P(z)}{Q(z)}\right\vert \leq \frac{M}{\left\vert z\right\vert^{m}}=\frac{M}{R^{m}}.
$$
A integração sobre o arco de circunferência se anula pois
$$
\left\vert \int_{C_{R}}\frac{P(z)}{Q(z)}dz\right\vert \leq \frac{M}{R^{m}}\int_{C_{R}}\left\vert dz\right\vert =\frac{\pi MR}{R^{m}}=\frac{\pi M}{R^{m-1}},
$$
que se anula quando \(R\rightarrow \infty\) pois \(m\geq 2\). Neste limite resta, portanto,
$$
\int_{-\infty }^{\infty }\frac{P(x)}{Q(x)}dx=\oint_{C}\frac{P(z)}{Q(z)}dz=2\pi i\sum_{k=1}^{n}\text{Res}( \frac{P(z)}{Q(z)},z_{k}),
$$
onde a soma é feita sobre todos os pólos do integrando no semiplano \(y\gt 0\).
Exercícios :
1. Calcule as integrais indefinidas:
$$
\begin{array}{lll}
\text{ a. }\;\; \int_{-\infty }^{\infty }\frac{dx}{x^{4}+1} &
\text{ b. }\;\; \int_{-\infty }^{\infty }\frac{dx}{ax^{2}+bx+c}, & a,b,c\in \mathbb{R}, b^{2}\lt 4ac. \\
\text{ c. }\;\; \int_0^{\infty }\frac{x^{2}dx}{x^{4}+9} &
\text{ d. }\;\; \int_{-\infty }^{\infty }\frac{dx}{x^{2}-x+1} &
\text{ e. }\;\; \int_0^{\infty }\frac{dx}{x^{6}+1}\; \\
\text{ f. }\;\; \int_{-\infty }^{\infty }\frac{xdx}{(x^{2}+4x+13)^{2}} &
\text{ g. }\;\; \int_0^{\infty }\frac{x^{2}dx}{(x^{2}+a^{2})^{2}}, a\gt 0, &
\text{ h. }\;\; \int_0^{\infty }\frac{x^{2}+1}{x^{4}+1}dx
\end{array}
$$
2) Mostre que \(\int_0^{\infty }\frac{dx}{(x^{2}+a^{2})(x^{2}+b^{2})}=\frac{\pi }{2ab( a+b)}\).
Algumas respostas e sugestões:
1a. \(\pi /\sqrt{2}\)
1b. \(2\pi /\sqrt{4ac-b^{2}}\)
1c. Observe que o integrando é par, logo \(\int_0^{\infty }=\frac{1}{2}\int_{-\infty }^{\infty }\).
1d. \(\pi \sqrt{2}/4\sqrt{3}\)
1f. \(-\pi /27\)
1g. \(\pi /4a\).
Antes de iniciarmos o estudo de séries de números e funções complexas faremos uma revisão destes conceitos utilizando números e funções reais, de variáveis reais. Para maiores detalhes consulte qualquer livro texto de Cálculo II.
Definiremos uma sequência infinita como um conjunto infinito de números que podem ser colocados em uma relação biunívoca com o conjunto dos números inteiros positivos. Denotaremos por \(\left\{a_n\right\}\) a uma sequência, sendo \(a_n\), com \(n=1,2,..\). os elementos individuais desta sequência.
Exemplo 1: Considere \(\left\{a_{n}\right\}\) a sequência com termo genérico \(a_{n}=1/n\). Neste caso
$$
\left\{a_{n}\right\} =\left\{1,\frac{1}{2},\frac{1}{3},\cdots \right\}.
$$
Observe que os termos desta sequência se aproximam de \(0\) para \(n\) suficientemente grande.
Definição: Dizemos que a sequência converge para um número \(L\), ou tem limite \(L\), se, dado qualquer número \(\varepsilon \gt 0\) existe um número \(N\) tal que
$$
n\gt N\Rightarrow \left\vert a_{n}-L\right\vert \lt\varepsilon.
$$
Usaremos como notação
$$
L=\lim_{n\rightarrow \infty }a_{n},\;\;\;\text{ ou }\;\; a_{n}\rightarrow L.
$$
Observe que, se \(\left\vert a_{n}-L\right\vert \lt\varepsilon\) então
$$
-\varepsilon \lt a_{n}-L\lt\varepsilon \Longleftrightarrow L-\varepsilon \lt a_{n}\lt L+\varepsilon.
$$
Portanto a convergência de uma sequência para um valor \(L\) significa que \(a_{n}\) fica arbitrariamente próximo de \(L\) quando se toma \(n\) suficientemente grande. Se uma sequência não converge para nenhum número dizemos que ela diverge.
Exemplo 2: A sequência do exemplo 1, \(a_n=1/n\) converge para \(L=0\).
Exemplo 3: A seguinte sequência converge para \(L=2/3\)
$$
a_{n}=\frac{2n^{2}+n-1}{3n^{2}-n}.
$$
Para ver isto dividimos o numerador e o denominador por \(n^{2}\),
$$
L=\lim_{n\rightarrow \infty }\frac{2n^{2}+n-1}{3n^{2}-n}=\lim_{n\rightarrow \infty }\frac{2+1/n-1/n^{2}}{3-1/n}=\frac{2}{3},
$$
onde usamos o fato de que \(1/n\rightarrow 0\) e \(1/n^{2}\rightarrow 0\).
Exemplo 4: A sequência \(\left\{\text{sen }n\right\}\) não converge para nenhum número, oscilando indefinidamente entre \(\,-1\) e \(1\). A sequência \(a_{n}=(n^{2}+1) /n\) também não converge pois tende a infinito com \(n\rightarrow \infty\).
Definiremos uma série infinita como a soma dos elementos de uma sequência infinita. Denotaremos a série por
$$
S=\sum_{n=0}^{\infty }a_{n}=a_0+a_{1}+a_{2}+a_{3}+\cdots.
$$
A soma de infinitos termos não tem um significado óbvio e imediato. Para atribuir a ela um sentido inequívoco definiremos antes a soma dos \(N\) primeiros termos da série, denominada a soma reduzida,
$$
S_{N}=\sum_{n=1}^{N}a_{n}.
$$
Observe agora que o conjunto destas somas reduzidas forma uma sequência \(\left\{S_{n}\right\} =S_{1},S_{2},S_{3},\cdots\), que pode convergir ou não. Dizemos que a série infinita converge para um número \(L\) se a sequência \(\left\{S_{n}\right\}\) converge para \(L\), ou seja,
$$
S_{n}\rightarrow L\Longleftrightarrow \sum_{n=1}^{\infty }a_{n}=L.
$$
Caso contrário a série diverge e denotamos
$$
\sum_{n=1}^{\infty }a_{n}=\infty \;\;\;\text{ ou }\;\;\sum_{n=1}^{\infty}a_{n}=-\infty,
$$
conforme o caso.
Exemplo 5: Um exemplo interesssante de uma série convergente é o seguinte:
$$
\sum_{n=0}^{\infty }\frac{1}{n!}=1+1+\frac{1}{2!}+\frac{1}{3!}+\cdots =\text{e},
$$
onde, por convenção, fazemos \(0!=1\). Este é um caso particular da série mais geral
$$
\sum_{n=0}^{\infty }\frac{x^{n}}{n!}=1+x+\frac{x^{2}}{2!}+\frac{x^{3}}{3!}+\cdots =\text{ e}^{x}.
$$
No último exemplo a função exponencial foi escrita como uma soma infinita de termos em potências de \(x\). As séries de potências são importantes no estudo das funções e suas aplicações.
Dizemos que uma série \(\sum_{n=0}^{\infty }a_{n}\) converge absolutamente se a série \(\sum_{n=0}^{\infty }\left\vert a_{n}\right\vert\) converge. Observe que toda a série absoluta convergente é convergente, isto é,
$$
\sum_{n=0}^{\infty }\left\vert a_{n}\right\vert \; \text{ converge } \Rightarrow \sum_{n=0}^{\infty }a_{n} \text{ converge.}
$$
Os seguintes testes são os mais utilizados para a verificação de convergencia de uma série.
Teste da Comparação: Se duas séries \(\Sigma a_n\) e \(\Sigma b_n\) são séries de termos não negativos (i.e. \(a_n\geq 0\) e \(b_n\geq 0\) para todo \(n)\) e \(a_n\leq\) \(b_n\) para todo \(n\), então
$$
\begin{array}{lll}
(i) & \;\;\text{ se }\;\;\;\Sigma b_n\text{ converge}\Rightarrow & \Sigma a_n\text{
converge} \\
(ii) & \;\;\text{ se }\;\;\;\Sigma a_n\;\;\text{diverge}\Rightarrow & \Sigma b_n\;\;\text{diverge.}
\end{array}
$$
Teste da Razão: \(\;\) Se \(\Sigma a_n\) é uma séries de termos positivos, definimos o limite
$$
R=\lim_{n\rightarrow \infty }\frac{a_{n+1}}{a_n}.
$$
Então, se
$$
\begin{array}{ll}
R \lt 1\Rightarrow & \Sigma a_n\text{ converge} \\
R \gt 1\Rightarrow & \Sigma a_n\;\;\text{diverge} \\
R=1, & \text{o teste é inconclusivo.}
\end{array}
$$
Teste da Integral: Se \(f(x)\) é uma função positiva não crescente para \(x\gt 0\), então a série \(\Sigma f(n)\) converge se, e somente se, a integral imprópria \(\int_1^\infty f(x)dx\) converge. Além disto vale a desigualdade
$$
\sum_{n=2}^Nf(n)\leq \int_1^Nf(x)dx\leq \sum_{n=1}^{N-1}f(n).
$$
Exemplo 6: Usamos o teste da razão para testar a convergência da série
$$
\sum_{n=1}^{\infty }\frac{n^{2}}{n!}.
$$
Temos, neste caso,
$$
a_{n}=\frac{n^{2}}{n!},\;\;a_{n+1}=\frac{( n+1)^{2}}{(n+1)!}
$$
Calculamos o limite
$$
R=\lim_{n\rightarrow \infty }\frac{( n+1)^{2}}{(n+1)!}\frac{n!}{n^{2}}=\lim_{n\rightarrow \infty }\frac{1}{n+1}( \frac{n+1}{n})
^{2}=\lim_{n\rightarrow \infty }\frac{n+1}{n^{2}}=0.
$$
Como \(R \lt 1\) concluimos que a série converge.
Uma função que pode ser expressa em termos de uma série infinita de potências em torno do ponto \(x=x_0\),
$$
f(x)=a_0+a_{1}( x-x_0) +a_{2}( x-x_0)
^{2}+\cdots =\sum_{n=0}^{\infty }a_{n}( x-x_0)^{n}
$$
é dita uma função analítica (neste ponto). Os coeficientes \(a_{n}\) podem ser obtidos do seguinte modo. Calcule o valor de \(f\) e suas derivadas no ponto \(x_0\)
$$
f(x_0)=a_0,
$$
$$
f'(x)=a_{1}+2a_{2}( x-x_0) +3( x-x_0)^{2}+\cdots =\sum_{n=1}^{\infty }na_{n}( x-x_0)^{n-1},
$$
$$
f'(x_0)=a_{1},
$$
$$
f^{\prime \prime }(x)=2a_{2}+2.3a_{3}( x-x_0) +\cdots=\sum_{n=2}^{\infty }n( n-1) a_{n}( x-x_0)^{n-2},
$$
$$
f^{\prime \prime }(x_0)=2a_{2}\Rightarrow a_{2}=\frac{1}{2}f^{\prime\prime }(x_0),
$$
$$
f^{(3)}(x)=2.3a_{3}( x-x_0) +\cdots =\sum_{n=3}^{\infty}n( n-1) ( n-2) a_{n}( x-x_0)^{n-3},
$$
$$
f^{(3)}(x)=2.3a_{3}\Rightarrow a_{3}=\frac{1}{6}f^{(3)}(x_0).
$$
Continuando este procedimento podemos calcular qualquer um dos coeficientes da série (1), obtendo
$$
a_{n}=\frac{1}{n!}f^{(n)}(x_0).
$$
Com estes coeficientes a série é a chamada série de Taylor,
$$
f(x)=\sum_{n=0}^{\infty }\frac{1}{n!}f^{(n)}(x_0)( x-x_0)^{n},
$$
onde \(f^{(n)}(x_0)\) indica a derivada n-ésima calculada no ponto \(x=x_0\). Uma série de Maclaurin é uma série de Taylor que descreve o comportamento de uma função em torno do ponto \(x_0=0\).
Resumindo: Sobre a série de potências \(S=\sum_{n=0}^{\infty} a_{n}( x-x_0)^{n}\) podemos coletar as seguintes propriedades:
(i) \(S\) converge (escolhido um valor para \(x\)) se existe o limite
$$
\lim_{N\rightarrow \infty }\sum_{n=0}^Na_n( x-x_0)^n.
$$
(ii) Se a série converge absolutamente, ou seja, existe o limite
$$
\lim_{N\rightarrow \infty }\sum_{n=0}^N\left| a_n( x-x_0)^n\right|,
$$
então ela converge.
(iii) Teste da razão: Definindo
$$
R=\lim_{n\rightarrow \infty }\left| \frac{a_{n+1}( x-x_0)^{n+1}}{a_n( x-x_0)^n}\right| =\left| x-x_0\right| \lim_{n\rightarrow
\infty }\left| \frac{a_{n+1}}{a_n}\right|
$$
então a série é absolutamente convergente no ponto \(x\) se \(R \lt 1\) e é divergente se \(R\gt 1\). O teste é inconclusivo se \(R=1\).
(iv) Se a série \(S\) converge em \(x=a\) então ela converge absolutamente para \(x\) no intervalo \(\left[ x-a,\;x+a\right]\). Se a série \(S\) diverge em \(x=a\) então ela diverge para \(x\) fora deste intervalo.
(v) O intervalo máximo de valores de \(x\) para os quais a série converge absolutamente é chamado o intervalo de convergência. O raio de convergência é \(\rho\) é definido de forma que \(\left[x_0-\rho ,x_0+\rho \right]\) é este intervalo.
Algumas considerações finais sobre o uso do sinal de somatório podem ser úteis. O índice usado pode ser substituído de acordo com as conveniências
$$
\sum_{i=1}^{N}a_{i}=\sum_{j=1}^{N}a_{j},
$$
e as parcelas da soma podem ser agrupadas ou isoladas, como nos exemplos a seguir:
$$
\sum_{i=1}^{N}a_{i}=\sum_{i=1}^{N-1}a_{i}+a_{N}=a_{1}+\sum_{i=2}^{N}a_{i},
$$
$$
\sum_{i=1}^{N}a_{i}=\sum_{i=1}^{P}a_{i}+\sum_{i=P+1}^{N}a_{i},\;\;1 \lt P \lt N.
$$
Pode ser mostrado por indução que
$$
\sum_{i=1}^{N}( a_{i}+b_{i})
=\sum_{i=1}^{N}a_{i}+\sum_{i=1}^{N}b_{i},
$$
$$
\sum_{i=1}^{N}ka_{i}=k\sum_{i=1}^{N}a_{i},\;\;\forall k\in \mathbb{R}.
$$
Se \(a_{i}=a\), uma constante, então
$$
\sum_{i=1}^{N}a_{i}=\sum_{i=1}^{N}a=Na.
$$
Uma série de potências, se convergente, pode ser derivada termo a termo e a derivada obtida desta forma será uma representação fiel da derivada da função que ela representa:
$$
y(x) =\sum_{n=0}^{\infty}a_{n}x^{n}=a_0+a_{1}x+a_{2}x^{2}+\cdots +a_{r}x^{r}+\cdots,
$$
$$
y^{\prime }( x) =\sum_{n=1}^{\infty}na_{n}x^{n-1}=a_{1}+2a_{2}x+\cdots +ra_{r}x^{r-1}+\cdots ,
$$
$$
y^{\prime \prime }(x) =\sum_{n=2}^{\infty }n( n-1)a_{n}x^{n-2}=2a_{2}x+\cdots +r(r-1) a_{r}x^{r-2}+\cdots.
$$
Uma série infinita de funções complexas é uma série
$$
s(z) =\sum_{n=0}^{\infty }f_{n}(z) =f_0(z) +f_{1}(z) +f_{2}(z) +\ldots
$$
onde as \(f_{i}(z)\) são funções complexas, de variáveis complexas e com um domínio comum. Definimos a soma parcial ou reduzida como
$$
s(z) =\sum_{n=0}^{N}f_{n}(z) =f_0(z)+f_{1}(z) +\ldots +f_{N}(z)
$$
e dizemos que a série converge se a sequência das somas parciais, \(\left\{s_0,\;s_{1},\;s_{2},\ldots \right\}\), converge, ou seja, quando existe o limite \(\lim_{n\rightarrow \infty }s_{n}(z)\). Neste caso
$$
s(z) =\sum_{n=0}^{\infty }f_{n}(z)=\lim_{n\rightarrow \infty }s_{n}(z).
$$
A expressão
$$
r_{n}(z) =s(z) -s_{n}(z)=\sum_{k=n+1}^{\infty }f_{k}(z)
$$
é denonimada o resto da série à partir de \(n+1\) e mede o quanto a soma parcial até o enésimo termo se aproxima da soma total.
Considere uma série
$$
s(z) =\sum_{n=0}^{\infty }f_{n}(z) ,
$$
convergente para todo \(z\) dentro de alguma região \(R\) do plano complexo. Então, dado \(\varepsilon \gt 0\) qualquer, para cada \(z\in R\), existe \(N\) tal que
$$
n\geq N\Rightarrow \left\vert s(z) -s_{n}(z)\right\vert \lt \varepsilon ,
$$
onde \(s_{n}(z)\) é a reduzida da série \(s(z)\). Observamos que \(N\) depende de \(\varepsilon\) também do ponto \(z\) onde a convergência é considerada.
Exemplo 7: Uma série geométrica é a soma dos termos de uma progressão geométrica,
$$
s(z) =\sum_{k=0}^{\infty }z^{k}=1+z+z^{2}+\ldots.
$$
Podemos verificar diretamente a convergência desta série e ainda encontrar a região de \(\mathbb{C}\) onde ela converge. Para fazer isto definimos a soma parcial, até o N-ésimo termo,
$$
s_{N}(z) =\sum_{k=0}^{N}z^{k}=1+z+z^{2}+\ldots +z^{N}.
$$
Multiplicando esta expressão por \(z\) temos
$$
zs_{N}(z) =\sum_{k=0}^{N}z^{k+1}=z+z^{2}+z^{3}+\ldots +z^{n+1}.
$$
Subtraindo as linhas acima
$$
s_{N}-zs_{N}=1-z^{N+1},
$$
ou seja, a soma parcial é dada por
$$
s_{N}(z) =\frac{1-z^{N+1}}{1-z}.
$$
Notamos agora que esta soma só converge se \(\left\vert z\right\vert \lt 1\). Neste caso o numerador da expressão acima tende para 1 e, portanto,
$$
s(z) =\sum_{n=0}^{\infty }z^{n}=\frac{1}{1-z}\text{ se }\left\vert z\right\vert \lt 1.
$$
Fora deste círculo ou na fronteira \(\left\vert z\right\vert =1\) a série diverge.
Observaremos, no entanto, que a convergência não é igual para todos os pontos dentro do círculo \(\left\vert z\right\vert \lt 1\). Escolhido um ponto \(z\) temos o resto
$$
r_{n}(z) =s(z) -s_{n}(z) =\frac{1}{1-z}-\frac{1-z^{n+1}}{1-z}=\frac{z^{n+1}}{1-z}.
$$
Em valor absoluto, devemos ter
$$
\left\vert s(z) -s_{n}(z) \right\vert =\frac{\left\vert z\right\vert^{n+1}}{\left\vert 1-z\right\vert } \lt \varepsilon
$$
para \(n \gt N\). Devemos indicar para que valor de \(N\) ocorre um erro menor que \(\varepsilon\). Queremos obter \(n\) em
$$
\left\vert z\right\vert^{n+1} \lt \varepsilon \left\vert 1-z\right\vert.
$$
Tome o logaritmo de base \(\left\vert z\right\vert\) dos dois lados da equação para obter
$$
n+1\gt \log _{\left\vert z\right\vert }( \varepsilon \left\vert
1-z\right\vert ) ,
$$
lembrando que \(\log _{\left\vert z\right\vert }\left\vert z\right\vert^{n+1}=n+1\) e o sinal de desigualdade fica invertido porque o logaritmo de base \(\left\vert z\right\vert \lt 1\) é uma função decrescente. Lembrando ainda que se pode mudar de base do logaritmo de acordo com a expressão
$$
\log _{a}N=\frac{\log _{b}N}{\log _{b}a}
$$
reecrevemos a expressão acima em termos do logaritmo natural
$$
n\gt\frac{\ln ( \varepsilon \left\vert 1-z\right\vert ) }{\ln\left\vert z\right\vert }-1
$$
o que mostra que não se pode determinar um único valor de \(N\) para todo o valor de \(\left\vert z\right\vert\), uma vez que a fração cresce arbitrariamente para \(\left\vert z\right\vert \rightarrow 1\). Em outras palavras a convergência é simples ou pontual. Não é possível determinar \(N\) para qualquer valor de \(z\) dentro do círculo de convergência.
Definição: (i) Uma sequência de funções \(f_{i}(z)\) definidas em um domínio comum \(D\), converge uniformemente para \(f(z)\) se, dado \(\varepsilon \gt 0\) existe um inteiro \(N\) tal que
$$
\forall z\in D,\ n\gt N\Rightarrow \left\vert f(z) -f_{n}(z) \right\vert \lt \varepsilon.
$$
(ii) A série \(s(z) =\sum_{n=0}^{\infty }f_{n}(z)\) converge uniformemente em \(D\) se, dado \(\varepsilon \gt 0\) existe \(N\) inteiro
tal que
$$
\forall z\in D,\ n\gt N\Rightarrow \left\vert s(z) -s_{n}(
z) \right\vert \lt \varepsilon.
$$
A diferença entre convergência pontual e uniforme é que, no segundo caso, a sequência ou a série fica arbitrariamentre próxima de seu valor limite para todos os valores de \(z\) dentro do domínio da função, a partir de algum \(n\) suficientemente grande.
Exemplo 8: Vimos que a série geométrica \(\sum_{n=0}^{\infty }z^{n}\) não converge uniformemente dentro do disco \(\left\vert z\right\vert \lt 1\). O motivo é que ela exige que se considere um número maior de termos a medida que se aproxima da borda do disco. Tal dificuldade desaparece se fixarmos o domínio \(\left\vert z\right\vert \leq \delta \lt 1\). Neste caso temos
$$
R_{n}=\frac{\left\vert z\right\vert^{n+1}}{\left\vert 1-z\right\vert }\leq
\frac{\delta^{n+1}}{1-\left\vert z\right\vert }\leq \frac{\delta^{n+1}}{1-\delta },
$$
que é menor que \(\varepsilon\) se tomarmos
$$
n \lt \frac{\ln ( \varepsilon \left\vert 1-\delta \right\vert ) }{\ln \delta }-1.
$$
Observe que, na obtenção da desigualdade (4), usamos
$$
\left\vert z_{1}+z_{2}\right\vert \geq \left\vert z_{1}\right\vert
-\left\vert z_{2}\right\vert \Rightarrow \left\vert 1-z\right\vert \geq
1-\left\vert z\right\vert.
$$
O seguinte teorema será útil na obtenção do teste M de Weierstrass que é, por sua vez, uma forma prática para se mostrar a convergência uniforme de uma sequência.
Teorema: Uma condição necessária e suficiente para a a série \(s(z) =\sum_{n=0}^{\infty }f_{n}(z)\) seja uniformemente convergente na região \(D\) é: dado \(\varepsilon \gt 0\) existe um \(N\) inteiro tal que, para todo \(p\) inteiro positivo temos
$$
\forall z\in D,\ n\gt N\Rightarrow \left\vert s_{n+p}(z)-s_{n}(z) \right\vert \lt \varepsilon.
$$
Observamos, antes de prosseguir com a demonstração, que
$$
s_{n+p}(z) -s_{n}(z) =\sum_{k=0}^{n+p}f_{k}(
z) -\sum_{k=0}^{n}f_{k}(z) =\sum_{k=n+1}^{n+p}f_{k}(
z) =f_{n+1}(z) +\ldots +f_{n+p}(z)
$$
e, portanto, a condição (5) equivale à
$$
\forall z\in D,\ n\gt N\Rightarrow \left\vert f_{n+1}(z) +\ldots
+f_{n+p}(z) \right\vert \lt \varepsilon.
$$
Demonstração: A condição é necessária pois, supondo que a série seja uniformemente convergente em \(D\) temos que, dado \(\varepsilon \gt 0\) existe um \(N\) tal que
$$
n\gt N\Rightarrow \left\vert s_{n}(z) -s(z) \right\vert \lt \varepsilon /2.
$$
Para um índice ainda maior vale certamente \(\left\vert s_{n+p}(z) -s(z) \right\vert \lt \varepsilon /2\), já que a série é convergente. Usando a desigualdade triangular temos
$$
\left\vert s_{n+p}-s_{n}\right\vert =\left\vert s_{n+p}-s+s-s_{n}\right\vert
\lt \left\vert s_{n+p}-s\right\vert +\left\vert s-s_{n}\right\vert \lt \varepsilon
/2+\varepsilon /2=\varepsilon.
$$
Além disto a condição é suficiente pois, supondo \(\left\vert s_{n+p}-s_{n}\right\vert \lt \varepsilon\) observamos que
$$
\lim_{p\rightarrow \infty }s_{n+p}(z) =s(z)
$$
e, portanto,
$$
\lim_{p\rightarrow \infty }\left\vert s_{n+p}-s_{n}\right\vert =\left\vert s-s_{n}\right\vert \lt \varepsilon.
$$
Tomando o limite com \(n\rightarrow \infty\) da mesma expressão temos
$$
\lim_{n\rightarrow \infty }\left\vert s-s_{n}\right\vert \lt \varepsilon ,
$$
que é a condição para que a série seja convergente.
Temos, como consequência do teorema acima temos o teste de Weierstrass:
Teorema: Se \(\sum M_{n}\) é uma série numérica convergente e \(f_{n}(z)\) uma sequência de funções definidas em \(D\), satisfazendo
$$
\left\vert f_{n}(z) \right\vert \leq M_{n},\forall n,\ \forall z\in D
$$
então \(\sum f_{n}(z)\) converge uniformemente em \(D\).
Demonstração: Usando a desigualdade triangular temos que
$$
\left\vert f_{n+1}+\ldots +f_{n+p}\right\vert \leq \left\vert
f_{n+1}\right\vert +\ldots +\left\vert f_{n+p}\right\vert \leq
M_{n+1}+\ldots +M_{n+p}\lt \varepsilon,
$$
onde a última desigualdade decorre de ser \(\sum M_{n}\) uma série convergente. Pelo teorema anterior \(\sum f_{n}(z)\) converge uniformemente em \(D\).
Exemplo 9: A série \(s=\sum_{n=0}^{\infty }z^{n}\) converge uniformemente no disco \(\left\vert z\right\vert \leq \delta \lt 1\) pois \(\left\vert z\right\vert \leq \delta^{n}=M_{n}\) e \(\sum_{n=0}^{\infty }\delta^{n}=1+\delta +\delta^{2}+\ldots =1/( 1-\delta )\) no disco.
Teorema: Seja \(f(z) =\sum_{n=0}^{\infty}f_{n}(z)\) uma série de funções uniformemente convergente em \(D\). Então
(i) Se as funções \(f_{i}(z)\) são contínuas \(f(z)\) é contínua em \(D\).
(ii) Se \(C\) é um contorno inteiramente contido em \(D\) então
$$
\int_{C}f(z) dz=\sum_{n=0}^{\infty }\int_{C}f_{n}(
z) dz.
$$
(iii) Se \(D\) é simplesmente conexa então \(f(z)\) é analítica em \(D\) e sua derivada é
$$
f'(z) =\sum_{n=0}^{\infty }f_{n}^{\prime }(
z).
$$
Sua derivada de ordem \(k\)-ésima é dada por
$$
\frac{d^{k}}{dz^{k}}f(z) =\sum_{n=0}^{\infty }\frac{d^{k}}{dz^{k}}f_{m}(z).
$$
Demonstração: (i) Tome \(\varepsilon \gt 0\) arbitrário e \(z\in D\) qualquer. Denotando a soma parcial e o resto respectivamente por
$$
s_{n}(z) =\sum_{k=0}^{n}f_{k}(z) ,\text{ }r_{n}(z) =\sum_{k=n+1}^{n}f_{k}(z)
$$
temos que \(f(z) =s_{n}(z) +r_{n}(z)\). Para mostrar que a soma infinita das funções é contínua
fazemos
$$
\begin{array}{ll}
\left\vert f(z) -f(z_0) \right\vert & \leq
\left\vert s_{n}(z) -s_{n}( z_0) \right\vert
+\left\vert r_{n}(z) -r_{n}( z_0) \right\vert
\; \\
& \leq \left\vert s_{n}(z) -s_{n}( z_0) \right\vert
+\left\vert r_{n}(z) \right\vert +\left\vert r_{n}(
z_0) \right\vert.
\end{array}
$$
Como a série converge uniformemente existe \(N\) tal que
$$
z\in D,\ n\gt N\Rightarrow \left\vert r_{n}(z) \right\vert \lt \varepsilon.
$$
Fixado um \(n=N,\;\;s_{N}(z)\) é contínua por ser a soma finita de funções contínuas e, portanto, dado \(\varepsilon \gt 0\) podemos determinar \(\delta\) tal que
$$
\left\vert z-z_0\right\vert \lt \delta \Rightarrow \left\vert s_{N}(z) -s_{N}( z_0) \right\vert \lt \varepsilon.
$$
Dai, e de (5), se pode concluir que
$$
\left\vert f(z) -f(z_0) \right\vert \leq \varepsilon +\varepsilon +\varepsilon =3\varepsilon ,
$$
o que significa que \(f(z)\) é contínua.
(ii) Observamos primeiro que, sendo \(f(z) =s_{n}(z) +r_{n}(z)\) temos
$$
\int_{C}f(z) dz=\int_{C}s_{n}(z) dz+\int_{C}r_{n}(z) dz=
$$
$$
\int_{C}\left[ \sum_{k=0}^{n}f_{k}(z) \right]
dz+\int_{C}r_{n}(z) dz=\sum_{k=0}^{n}\int_{C}f_{k}(
z) dz+\int_{C}r_{n}(z) dz,
$$
onde se usou o fato de que a integral da soma finita de funções é a soma das integrais. Observamos agora que a última integral tende a zero para \(n\rightarrow \infty\), o que é mais fácil ser mostrado em valor absoluto:
$$
\left\vert \int_{C}r_{n}(z) dz\right\vert \leq \int_{C}\left\vert r_{n}(z) \right\vert \left\vert dz\right\vert \leq \varepsilon L,
$$
onde fizemos \(\left\vert r_{n}(z) \right\vert \leq \varepsilon\) e \(\int_{C}\left\vert dz\right\vert =L\), é o comprimento de arco do
contorno \(C\). Tomando \(n\rightarrow \infty\) e lembrando que \(\left\vert r_{n}(z) \right\vert \underset{n\rightarrow \infty }{\rightarrow}0\) temos o resultado desejado:
$$
\int_{C}f(z) dz=\sum_{n=0}^{\infty }\int_{C}f_{n}(z) dz.
$$
(iii) Como cada uma das funções \(f_{k}\) é analítica então
$$
\oint f_{k}(z) dz=0,\ k=0,~1,~2,\;\ldots.
$$
Como consequência \(\oint_{C}f(z) dz=\sum_{k=0}^{\infty }\oint_{C}f_{k}(z) dz=0\) para uma contorno fechado \(C\) arbitrário em \(D\). Pelo teorema de Morera concluímos que \(f\) é analítica. Resta mostrar que \(f’=\sum f_{k}^{\prime }\). Escolhido um \(z\in R\) e \(C\) um contorno envolvendo \(z\) uma vez no sentido positivo (podemos tomar, por exemplo \(C:\left\vert w-z\right\vert =\delta )\) temos que a série
$$
\frac{k!}{2\pi i}\frac{f(w) }{( w-z)^{k+1}}=\frac{k!}{2\pi i}\sum_{n=0}^{\infty }\frac{f_{n}( w) }{( w-z)
^{k+1}}
$$
converge uniformemente para \(w\) sobre o contorno \(C\). Logo ela pode ser integrada termo a termo. Usando a fórmula da derivada \(k-\)ésima temos
$$
f^{( k) }(z) =\frac{k!}{2\pi i}\oint\nolimits_{C}\frac{f(w) }{( w-z)^{k+1}}dw=
$$
$$
f^{( k) }(z) =\frac{k!}{2\pi i}\oint\nolimits_{C}\frac{\sum_{n=0}^{\infty }f_{n}( w) }{( w-z)^{k+1}}dw=
$$
$$
=\frac{k!}{2\pi i}\sum_{n=0}^{\infty }\oint\nolimits_{C}\frac{f_{n}( w) }{( w-z)^{k+1}}dw=\sum_{n=0}^{\infty } f_{n}^{(k) }(z),
$$
como queríamos mostrar.
Um tipo particular de série de funções é obtido quando as funções envolvidas são simplesmente potências, \(f_{n}(z) =a_{n}(z-z_0)^{n}\). Neste caso temos as séries de potências,
$$
f(z) =\sum\limits_{n=0}^{\infty }a_{n}(z-z_0)
^{n},\ \ a_{n},\ z_0\in \mathbb{C}.
$$
Esta é a chamada série de Taylor para função \(f(z)\) e seus coeficientes \(a_{n}\) podem ser obtidos, como veremos, de modo análogo ao usado nas séries de funções reais. Em alguns casos, no entanto, podemos obter a séries por comparação com séries previamente conhecidas, como ilustraremos nos exemplos a seguir.
Exemplo 10: Conhecemos a expansão em séries
$$
\frac{1}{1-z}=\sum\limits_{n=0}^{\infty }z^{n},\ \ \left\vert z\right\vert \lt 1.
$$
Fazendo \(u=-z\) na expressão acima temos
$$
\frac{1}{1+u}=\sum\limits_{n=0}^{\infty }( -u)
^{n}=\sum\limits_{n=0}^{\infty }( -1)^{n}u^{n},\ \ \left\vert
u\right\vert \lt 1.
$$
As duas séries convergem dentro do mesmo disco de raio unitário.
Exemplo 11: Podemos obter por comparação a expansão em séries de \(f(z) =1/z\) em torno de \(z_0=2\), ou seja, em potências de \(z-2\) da seguinte forma:
$$
\frac{1}{z}=\frac{1}{z-2+2}=\frac{1/2}{1+( z-2) /2}.
$$
Denotando \(u=( z-2) /2\) temos
$$
\frac{1}{z}=\frac{1}{2}\frac{1}{1+u}=\frac{1}{2}\sum\limits_{n=0}^{\infty
}( -1)^{n}u^{n}=\frac{1}{2}\sum\limits_{n=0}^{\infty }(
-1)^{n}( \frac{z-2}{2})^{n}=\sum\limits_{n=0}^{\infty }\frac{( -1)^{n}}{2^{n+1}}( z-2)^{n},
$$
válida na região
$$
\left\vert \frac{z-2}{2}\right\vert \lt 1\Rightarrow \left\vert z-2\right\vert \lt 2,
$$
ou seja, o disco de raio \(2\) com centro em \(z=2\). Observe que não é possível obter a série de potências, dada pela equação (6), da função \(f(z) =1/z\) em torno de \(z_0=0\), uma vez que, neste ponto, a função não é analítica e nem sequer está definida.
Exemplo 12: A expansão em séries de \(f(z) =1/z\) em potências de \(z+3\) pode ser obtida da seguinte forma:
$$
\frac{1}{z}=\frac{1}{z+3-3}=\frac{-1/3}{1-( z+3) /3}.
$$
Denotando \(u=( z+3) /3\) temos
$$
\frac{1}{z}=-\frac{1}{3}\frac{1}{1-u}=-\frac{1}{3}\sum\limits_{n=0}^{\infty}u^{n}=-\frac{1}{3}\sum\limits_{n=0}^{\infty }( \frac{z+3}{3})
^{n}=-\sum\limits_{n=0}^{\infty }\frac{1}{3^{n+1}}( z+3)^{n},
$$
válida na região
$$
\left\vert \frac{z+3}{3}\right\vert \lt 1\Rightarrow \left\vert z+3\right\vert \lt 3.
$$
Exemplo 13: A função \(f(z)=1/( 6z-3)\) tem a seguinte expansão em torno de \(z_0=2\) :
$$
\frac{1}{6z-3}=\frac{1}{6( z-2) +9}=\frac{1/9}{1+2(
z-2) /3}.
$$
Denotando \(u=2( z-2) /3\) temos
$$
f(z) =\frac{1}{9}\frac{1}{1+u}=\frac{1}{9}\sum\limits_{n=0}^{\infty}(-1)^{n}u^{n}=
$$
$$
=\frac{1}{9}\sum\limits_{n=0}^{\infty}(-1)^{n}(\frac{2}{3})^{n}(z-2)^{n}=\sum\limits_{n=0}^{\infty }( -1)^{n}\frac{2^{n}}{3^{n+2}}( z-2)^{n}.
$$
Esta expansão é válida na região \(\left\vert z-2\right\vert \lt 3/2\).
Definição: Os valores de \(z\) para os quais a série converge absolutamente é a região de convergência da série. Se esta região é o disco \(\left\vert
z-z_0\right\vert \lt r\) então dizemos que \(r\) é o raio de convergência da série.
Teorema: O raio de convergência de \(s=\sum\limits_{n=0}^{\infty }a_{n}(z-z_0)^{n}\;\) é dado por
$$
r=\lim_{n\rightarrow \infty }\left\vert \frac{a_{n}}{a_{n+1}}\right\vert ,
$$
quando este limite existir.
Demonstração: Sabemos que a série dada converge se \(\sum\limits_{n=0}^{\infty }\left\vert a_{n}(z-z_0)^{n}\; \right\vert\) converge. Pelo teste da razão esta última série converge se
$$
L=\lim_{n\rightarrow \infty }\left\vert \frac{a_{n+1}(z-z_0)
^{n+1}}{a_{n}(z-z_0)^{n}}\right\vert \lt 1\Rightarrow
\lim_{n\rightarrow \infty }\frac{\left\vert a_{n+1}\right\vert }{\left\vert
a_{n}\right\vert }\frac{\ \left\vert z-z_0\right\vert^{n+1}}{\left\vert
z-z_0\right\vert^{n}}\lt 1,
$$
ou ainda
$$
\lim_{n\rightarrow \infty }\frac{\left\vert a_{n}\right\vert }{\left\vert
a_{n+1}\right\vert }\frac{1}{\left\vert z-z_0\right\vert }\gt 1\Rightarrow
\lim_{n\rightarrow \infty }\frac{\left\vert a_{n}\right\vert }{\left\vert
a_{n+1}\right\vert }\gt \left\vert z-z_0\right\vert.
$$
Estes são os valores de \(z\) para os quais a série dada converge, ou
seja,
$$
\left\vert z-z_0\right\vert \lt r=\lim_{n\rightarrow \infty }\frac{\left\vert
a_{n}\right\vert }{\left\vert a_{n+1}\right\vert }.
$$
Exemplo 14: Vamos encontrar o raio de convergência da série \(\sum\nolimits_{n=1}^{\infty }( \sqrt{n})^{n}z^{n}\). Temos, neste caso, que \(a_{n}=n^{n}/2\) e, portanto,
$$
r=\lim_{n\rightarrow \infty }\frac{n^{n/2}}{( n+1)^{(
n+1) /2}}=\lim_{n\rightarrow \infty }\left[ \frac{n^{n}}{(
n+1)^{n+1}}\right]^{1/2}=
$$
$$
=\lim_{n\rightarrow \infty }\left[ \frac{n^{n}}{( n+1)^{n}(
n+1) }\right]^{1/2}=\lim_{n\rightarrow \infty }\frac{1}{(
n+1)^{1/2}}( \frac{n}{( n+1) })^{n/2}=0.
$$
O raio de convergência nulo indica que esta série diverge para qualquer valor de \(z\neq 0\).
Exercícios:
1. Mostre que
$$
\begin{array}{ll}
\text{a.}\; \frac{1}{( 1-z)^{2}}=\sum\limits_{n=0}^{\infty}( n+1) z^{n}\; & \text{b.}\; \ln (1-z)=-\sum\limits_{n=1}^{\infty }\frac{z^{n}}{n} \\
\text{c.}\; \frac{1}{1+z}=\sum\limits_{n=0}^{\infty}(-1)^{n}z^{n} & \text{d.}\; \frac{1}{1-z^{2}}=\sum\limits_{n=0}^{\infty}z^{2n}\; \\
\text{e.}\; \ln ( 1+z) =\sum\limits_{n=1}^{\infty }\frac{( -1)^{n+1}}{n}z^{n}.\; &
\end{array}
$$
2. Use o teste de Weierstrass para testar a convergência dasseguintes séries:
$$
\begin{array}{ll}
\text{a. }\ \sum\limits_{n=1}^{\infty }\frac{n\cos 3n}{1+5n}z^{n},\; \text{ no disco }\left\vert z\right\vert \leq r\lt 1,\;
& \text{b. }\; \sum\limits_{n=1}^{\infty }\frac{n^{2}-2\cos n}{10n^{2}+7}z^{2n-1},\; \text{ no disco }\left\vert z\right\vert \leq r\lt 1,\\
\text{c. }\; \sum\limits_{n=1}^{\infty }\frac{n+7\sqrt{n+1}}{(n+1) 2^{n}}z^{2n-1},\; \text{ no disco }\left\vert z\right\vert \leq r\lt \sqrt{2},
& \text{d. }\; \sum\limits_{n=1}^{\infty }\frac{( -1)^{n}n( z-1)^{n}}{n+1}\; ,\ \text{no disco }\left\vert z-1\right\vert \leq r\lt 1, \\
\text{e. }\; \sum\limits_{n=1}^{\infty }\frac{n^{k}}{R^{n}}z^{n},\; \text{ no disco } \left\vert z\right\vert \leq r\lt R,\; \text{ quaisquer }R\;\text{ e }k.
& \text{f. }\; \sum\limits_{n=1}^{\infty }\frac{a^{n}}{n!}z\;^{n},\; \text{ no disco }\left\vert z\right\vert \lt R,\; \text{ quaisquer }R \;\text{ e }\;\;\ a.
\end{array}
$$
3. Obtenha o desenvolvimento em séries de potências em torno do ponto indicado. Represente graficamente a região de convergência.
$$
\begin{array}{l}
\text{a. }\; f(z) =\frac{1}{z} \; \text{ em potências de }\;z+i,\; \\
\text{b. }\; f(z) =\frac{1}{2z-9} \; \text{ em torno de }\;z_0=3,\; \; \\
\text{c. }\; f(z) =\frac{1}{z^{2}} \; \text{ em potências de }\;z-1,\; \; \\
\text{d. }\; f(z) =\frac{1}{2z-3} \; \text{ em torno de }\;z_0=-i.\; \;
\end{array}
$$
4.) Encontre o raio de convergência das séries:
$$
\begin{array}{ll}
\text{a. }\ \sum\limits_{n=0}^{\infty }nz^{n}\; & \text{b. }\
\sum\limits_{n=0}^{\infty }n!z^{n}\; \\
\text{c. }\ \sum\limits_{n=0}^{\infty }\frac{( z-i)^{n}}{n} &
\text{d. }\ \sum\limits_{n=0}^{\infty }\ln ( 3n^{2}+5) (
z\; +i)^{n} \\
\text{e. }\ \sum\limits_{n=0}^{\infty }( \text{ senh }n) z^{n}\; & \text{f. }\ \sum\limits_{n=1}^{\infty }\frac{4^{n}}{n}z^{2n}
\end{array}
$$
Algumas respostas e sugestões:
1.(a, b) Derive e integre termo a termo a série geométrica
1.(c) Faça \(u=-z\). (d) Faça \(u=z^{2}\). (e) Faça \(u=-z\) na série obtida em (1b).
2. Todas as séries convergem nas regiões indicadas.
3a. \(f(z)=\sum\limits_{n=0}^{\infty}(i)^{1-n}(z+i)^{n},\;\;\left\vert z+i\right\vert \lt 1.\)
3b. \(f(z)=\sum\limits_{n=0}^{\infty}\frac{-2^{n}}{3^{n+1}}( z-3)^{n},\;\; \left\vert z-3\right\vert \lt \frac{3}{2}.\)
3c. \(f(z)=\sum\limits_{n=0}^{\infty}(-1)^{n}(n+1)(z-1)^{n},\;\; \left\vert z-1\right\vert \lt 1.\) (Encontre a expressão para \(1/z\) e derive.)
3d. \(f(z)=\sum\limits_{n=0}^{\infty}\frac{-2^{n}}{( 3+2i)^{n+1}}( z+i)^{n},\;\;\left\vert z+i\right\vert \lt \frac{\sqrt{13}}{2}\).
4a. \(r=1\), 4b. \(r=0\), 4c. \(r=\infty\), 4d. \(r=1\), 4e. \(r=1/e\), 4f. \(r=1/2\).
Teorema: Toda série de potências
$$
f(z) =\sum\limits_{n=0}^{\infty }a_{n}(z-z_0)^{n}
$$
representa uma função analítica em seu disco de convergência \(\left\vert z-z_0\right\vert \lt r\). Esta série pode ser derivada termo a termo um número \(n\) arbitrário de vezes e as derivadas possuem o mesmo raio de convergência da série original. Por exemplo, a derivada primeira é
$$
f'(z) =\sum\limits_{n=1}^{\infty }na_{n}(
z-z_0)^{n-1}=\sum\limits_{n=0}^{\infty }( n+1)
a_{n+1}(z-z_0)^{n},
$$
enquanto a derivada segunda é
$$
f^{\prime \prime }(z) =\sum\limits_{n=2}^{\infty }n(
n-1) a_{n}(z-z_0)^{n-2}=\sum\limits_{n=0}^{\infty
}( n+1) ( n+2) a_{n+2}(z-z_0)^{n}.
$$
Teorema: Seja \(f\) uma função analítica em uma região \(R\). Então \(f\) possui um desenvolvimento único em série de potências dado por
$$
f(z) =\sum\limits_{n=0}^{\infty }\frac{f^{( n) }( z_0) }{n!}(z-z_0)^{n},
$$
onde \(z_0\in R\) e \(\left\vert z-z_0\right\vert \leq r_0\) é um disco inteiramente contido em \(R\).
Demonstração: Seja \(z\) um ponto no interior do disco \(\left\vert z-z_0\right\vert \leq r_0\), como se mostra na figura 1. Denote \(r=\left\vert z-z_0\right\vert\) e escolha \(r_{1}\) de modo que \(r\lt r_{1}\lt r_0\). Como \(f\) é analítica em \(R\), pela fórmula de Cauchy
$$
f(z) =\frac{1}{2\pi i}\oint\limits_{C_{1}}\frac{f(w)}{w-z}dw, \;\text{ onde }\; C_{1}:\left\vert w-z_0\right\vert=r_{1}.
$$
Observe ainda que
$$
\frac{1}{w-z}=\frac{1}{( w-z_0) -(z-z_0) }=\frac{1}{w-z_0}\frac{1}{1-(z-z_0)/( w-z_0) }=
$$

$$
=\frac{1}{w-z_0}\sum\limits_{n=0}^{\infty }(\frac{z-z_0}{w-z_0})^{n},
$$
que é uma série convergente porque
$$
\left\vert \frac{z-z_0}{w-z_0}\right\vert =\frac{\left\vert z-z_0\right\vert }{\left\vert w-z_0\right\vert }=\frac{r}{r_{1}} \lt 1.
$$
Concluimos que
$$
\frac{1}{w-z}=\sum\limits_{n=0}^{\infty }\frac{(z-z_0)^{n}}{( w-z_0)^{n+1}}.
$$
O integrando na equação (8) pode ser escrito como
$$
\frac{f(w) }{w-z}=f(w) \sum\limits_{n=0}^{\infty }\frac{f(w) (z-z_0)^{n}}{( w-z_0)
^{n+1}}.
$$
Como \(f(z)\) é contínua ela deve assumir um valor finito máximo em \(C_{1}\), ou seja, \(\left\vert f(w)
\right\vert \leq M\) e
$$
\sum\limits_{n=0}^{\infty }\left\vert \frac{f(w) (
z-z_0)^{n}}{( w-z_0)^{n+1}}\right\vert \leq \frac{M}{r_{1}}\sum\limits_{n=0}^{\infty }( \frac{r}{r_{1}})^{n}.
$$
Pelo teste de Weierstrass a série converge e, portanto, pode ser integrada termo a termo,
$$
f(z) =\frac{1}{2\pi i}\oint\limits_{C_{1}}f(w)
\sum\limits_{n=0}^{\infty }\frac{(z-z_0)^{n}}{(
w-z_0)^{n+1}}dw=\sum\limits_{n=0}^{\infty }\left[ \frac{1}{2\pi i}\oint\limits_{C_{1}}\frac{f(w) }{( w-z_0)^{n+1}}dw\right] (z-z_0)^{n}.
$$
O termo dentro de colchetes é \(f^{( n) }( z_0)/n!\) de onde concluímos a demonstração de que
$$
f(z) =\sum\limits_{n=0}^{\infty }\frac{f^{( n)
}( z_0) }{n!}(z-z_0)^{n}.
$$
A série obtida, equação (7), é denominada série de Taylor. A expansão em séries de potência para uma função em torno de \(z_0=0\) é denominada série de MacLaurin.
Exemplo 15: A expansão em séries de potência para a função exponencial \(f(z) =\text{ e}^{z}\) em torno de \(z_0=0\) pode ser encontrada da seguinte forma:
$$
f^{( n) }(z) =\text{ e}^{z};\ f^{( n) }(0) =1.
$$
Então
$$
\text{ e}^{z}=1+z+\frac{z^{2}}{2!}+\ldots +\frac{z^{n}}{n!}+\ldots=\sum\limits_{n=0}^{\infty }\frac{z^{n}}{n!}.
$$
Exemplo 16: (Série binomial) Considere a função \(f(z) =( 1+z)^{\alpha }\), no ramo \(f(0)=1\). Em torno de \(z_0=0\) podemos calcular
$$
f'(z) =\alpha ( 1+z)^{\alpha -1},\ \
f'( 0) =\alpha ,
$$
$$
f^{\prime \prime }(z) =\alpha ( \alpha -1) (
1+z)^{\alpha -2},\ \ f^{\prime \prime }( 0) =\alpha
( \alpha -1) ,
$$
$$
f^{( n) }(z) =\alpha ( \alpha -1) \cdots
( \alpha -n+1) ( 1+z)^{\alpha -n},\ \ f^{(
n) }( 0) =\alpha ( \alpha -1) \cdots (
\alpha -n+1).
$$
Portanto
$$
( 1+z)^{\alpha }=1+\alpha z+\frac{\alpha ( \alpha -1) }{!}z^{2}+\cdots =\sum\limits_{n=0}^{\infty }(
\begin{array}{c} \alpha \\
n\end{array}) z^{n}.
$$
onde
$$
(
\begin{array}{c}
\alpha \\
n\end{array}) =\frac{\alpha ( \alpha -1) \cdots ( \alpha
-n+1) }{n!}
$$
é o coeficiente binomial. Se \(\alpha\) é inteiro então a série termina no termo \(n=\alpha\).
Exercícios:
1. Encontre as séries de potências em torno de \(z_0=0\) de: a. \(\text{sen }z\), b. \(\cos z\), c. \(\text{ senh }z\), d. \(\cosh z\).
2. Desenvolva em torno de \(z_0=1\) a função \(f(z) =z\ln z-z\). (Use a determinação ou ramo principal, no qual \(\ln 1=0\)).
3. Desenvolva em séries de potências de \(z\) e \(( z-2)\) as funções
$$
f(z) =\frac{1}{( 4-z)^{3}};\ \ g(z) =\frac{1}{z^{5}}.
$$
Algumas respostas e sugestões:
$$
\begin{array}{ll}
\text{1a. } \text{sen }z=\sum\limits_{n=0}^{\infty }\frac{(-1)^{n}}{(2n+1) !}z^{2n+1}\; &
\text{1b. } \cos z=\sum\limits_{n=0}^{\infty }\frac{(-1)^{n}}{(2n)!}z^{2n}\; \\
\text{1c. } \text{ senh }z=\sum\limits_{n=0}^{\infty }\frac{z^{2n+1}}{(2n+1)!} &
\text{1d. }\ \cosh z=\sum\limits_{n=0}^{\infty }\frac{z^{2n}}{(2n)!}
\end{array}
$$
3) Observe que \(f(z) =( 1/4^{3}) /( 1-z/4)^{3}\) e aplique o desenvolvimento binomial. Alternativamente desenvolva \(1/( 4-z)\) em potências de \(z\) e derive duas vezes.
Séries de Laurent
Podemos notar que uma função não analítica em torno de um ponto \(z_0\) pode ter um desenvolvimento em séries em torno deste ponto se admitirmos potências com expoentes negativos. Para ver isto com maior clareza consideremos um exemplo.
Exemplo 17: A função \(f(z) =\text{ e}^{z}/z^{3}\) não é analítica em \(z=0\) e portanto não possui expansão de Taylor em torno deste ponto. No entanto podemos escrever
$$
\frac{\text{ e}^{z}}{z^{3}}=\frac{1}{z^{3}}( 1+z+\frac{z^{2}}{2!}+\ldots +\frac{z^{n}}{n!}+\ldots ) \frac{1}{z^{3}}+\frac{1}{z^{2}}+\frac{1}{2!z}+\frac{1}{3!}+\frac{z}{4!}+\frac{z^{2}}{5!}+\ldots.
$$
Podemos também escrever diretamente
$$
\frac{\text{ e}^{z}}{z^{3}}=\frac{1}{z^{3}}\sum\limits_{n=0}^{\infty }\frac{z^{n}}{n!}=
\sum\limits_{n=0}^{\infty }\frac{z^{n-3}}{n!}=\sum\limits_{n=-3}^{\infty }\frac{z^{n}}{( n+3) !}.
$$
Esta série, incluindo termos em potências negativas de \(z\), generaliza a série de Taylor e é chamada Série de Laurent.
Teorema: Seja \(f\) uma função univalente e analítica na região anular \(G:r\lt \left\vert z-z_0\right\vert \lt R\). Então, \(\forall z\in G\) vale$$
f(z) =\sum\limits_{n=1}^{\infty }\frac{a_{-n}}{(z-z_0)^{n}}+\sum\limits_{n=0}^{\infty }a_{n}(z-z_0)^{n}=\sum\limits_{n=-\infty }^{\infty }a_{n}(z-z_0)^{n},
$$
onde os coeficientes \(a_{n}\) são dados por
$$
a_{n}=\frac{1}{2\pi i}\oint\limits_{C}\frac{f(w) }{(w-z_0)^{n+1}}dw
$$
sendo \(C\) um contorno fechado envolvendo \(z_0\) uma vez, no sentido positivo.
Demonstração: Representamos na figura 2 a região anular \(G\) limitada pelos círculos de raio \(r\) e \(R\), e \(z\in G\). Construímos dois caminhos \(C_{1}\) e \(C_{2}\), de raios \(r_{1}\) e \(r_{2}\) respectivamente, e o caminho \(\gamma =C_{2}\cup -C_{1}\cup L\cup -L\) de forma que \(f\) seja analítica em \(\gamma\) e seu interior. Como \(f\) é analítica em \(G\) podemos usar a fórmula da integral,
$$
f(z) =\frac{1}{2\pi i}\oint\limits_{\gamma }\frac{f(w) }{w-z_0}dw.
$$
Esta integral pode ser escrita como a soma
$$
f(z) =\frac{1}{2\pi i}\oint\limits_{C_2}\frac{f(w) }{w-z_0}dw-\frac{1}{2\pi i}\oint\limits_{C_1}\frac{f(w) }{w-z_0}dw,
$$
lembrando que as integrais sobre \(L\) e \(-L\) se cancelam.

A primeira integral, sobre o caminho \(C_2\), é a mesma já tratada na demonstração do teorema de Taylor, resultando em
$$
\frac{1}{2\pi i}\oint\limits_{C_2}\frac{f(w)}{w-z_0}dw=\sum\limits_{n=0}^{\infty }a_{n}(z-z_0)^{n},\ \text{onde }\ a_{n}=\frac{f^{( n) }( z_0) }{n!}.
$$
Para resolver a segunda integral, que denotaremos por \(I_{2}\), escrevemos
$$
\frac{1}{w-z}=\frac{1}{( w-z_0) -(z-z_0) }=\frac{-1/(z-z_0) }{1-( w-z_0) /(z-z_0) }
$$
$$
=-\sum\limits_{n=0}^{\infty }\frac{( w-z_0)^{n}}{(z-z_0)^{n+1}},
$$
uma série que converge uniformemente para todo \(w\) em \(C_{1}\) pois
$$
\left\vert \frac{w-z_0}{z-z_0}\right\vert =\frac{\left\vert
w-z_0\right\vert }{\left\vert z-z_0\right\vert }=\frac{r_{1}}{r}\lt 1.
$$
Desta forma podemos escrever
$$
I_{2}=\frac{-1}{2\pi i}\oint\limits_{C_{1}}\frac{f(w) }{w-z}dw=\frac{1}{2\pi i}\oint\limits_{C_{1}}f(w)
\sum\limits_{n=0}^{\infty }\frac{( w-z_0)^{n}}{(
z-z_0)^{n+1}}dw=
$$
$$
=\frac{1}{2\pi i}\sum\limits_{n=0}^{\infty }\frac{1}{(z-z_0)
^{n+1}}\oint\limits_{C_{1}}\frac{f(w) dw}{( w-z_0)
^{-n}}.
$$
Trocando o índice de \(n\) para \(n+1\) temos
$$
I_{2}=\frac{1}{2\pi i}\sum\limits_{n=1}^{\infty }\frac{1}{(
z-z_0)^{n}}\oint\limits_{C_{1}}\frac{f(w) dw}{(
w-z_0)^{-n+1}}=\sum\limits_{n=1}^{\infty }\frac{a_{-n}}{(
z-z_0)^{n}}=\sum\limits_{n=-\infty }^{-1}a_{n}(z-z_0)
^{n}.
$$
Observe que, nos dois casos, as constantes podem ser expressas por
$$
a_{n}=\frac{1}{2\pi i}\oint\limits_{C}\frac{f(w) dw}{(
w-z_0)^{n+1}},
$$
onde \(C\) pode ser qualquer caminho que envolve \(z_0\) uma vez, no sentido positivo.
Algumas vezes, da mesma forma que ocorre com as expansões em séries de Taylor para funções analíticas, é possível encontrar a série de Laurent por simples manipulação da função dada e comparação com a série geométrica. Para mostrar isto vejamos um exemplo.
Exemplo 18: Vamos obter série de Laurent para a função
$$
f(z) =\frac{1}{z^{2}-3z+2},
$$
em torno de \(z_0=1\), na região \(0\lt \left\vert z-1\right\vert \lt 1\). Escrevemos a função como
$$
f(z) =\frac{1}{( z-1) ( z-2) },
$$
e observamos que \(1/( z-2)\) é analítica em \(z_0=1\) e pode ser escrita como
$$
\frac{1}{z-2}=\frac{1}{z-1-1}=\frac{-1}{1-( z-1) }=-\sum\limits_{n=0}^{\infty }( z-1)^{n},
$$
válida para \(\left\vert z-1\right\vert \lt 1\). Como consequência
$$
f(z) =\frac{1}{z-1}\frac{1}{z-2}=\frac{-1}{z-1}\sum\limits_{n=0}^{\infty }( z-1)
^{n}=-\sum\limits_{n=0}^{\infty }( z-1)^{n-1},
$$
que é a série de Laurent para esta função na região indicada. Esta série pode também ser escrita como
$$
f(z) =-\sum\limits_{n=-1}^{\infty }( z-1)^{n}.
$$
Alternativamente, o mesmo exercício pode ser feito do seguinte modo: escrevemos, por meio de frações parciais
$$
f(z) =\frac{1}{( z-1) ( z-2) }=\frac{1}{z-2}-\frac{1}{z-1}.
$$
A série de Taylor para o primeiro termo, analítico, já foi encontrada. Temos portanto a mesma série já encontrada,
$$
f(z) =-\frac{1}{z-1}-\sum\limits_{n=0}^{\infty }(z-1)^{n}.
$$
Exemplo 19: Vamos obter série de Laurent para a mesma função do exemplo anterior, \(f(z)=(z^2-3z+2)^{-1}\) em torno de \(z_0=1\), mas desta vez na região \(\left\vert z-1\right\vert \gt 1\). Agora o ponto \(z_0=2\) está dentro da região de interesse e \(1/(z-2)\) não é analítica. Fazemos
$$
\frac{1}{z-2}=\frac{1}{z-1-1}=\frac{1/( z-1) }{1-1/(z-1) }=\frac{1}{z-1}\frac{1}{1-u}=\frac{1}{z-1}\sum\limits_{n=0}^{\infty }u^{n},
$$
onde
$$
u=\frac{1}{z-1},\;\; \text{válida para }\;\; \left\vert u\right\vert \lt 1\Rightarrow \left\vert z-1\right\vert \gt 1,
$$
que é a região onde se espera que a série seja convergente. Como consequência
$$
\frac{1}{z-2}=\frac{1}{z-1}\sum\limits_{n=0}^{\infty }( \frac{1}{z-1})^{n}=\sum\limits_{n=0}^{\infty }\frac{1}{( z-1)^{n+1}}.
$$
A série que buscamos é
$$
f(z) =\frac{1}{z-1}\sum\limits_{n=0}^{\infty }\frac{1}{(
z-1)^{n+1}}=\sum\limits_{n=0}^{\infty }\frac{1}{( z-1)
^{n+2}}=\sum\limits_{n=-\infty }^{-2}( z-1)^{n}.
$$
As séries de Laurent generalizam as séries de Taylor para o tratamento de funções que possuem algum ponto de não analiticidade dentro da região considerada. Observe que, se \(f\) é analítica em toda parte, inclusive para \(\left\vert z-z_0\right\vert \leq r\), então os coeficientes \(a_{n}\) com \(n\) negativo são todos
nulos. Por exemplo:
$$
a_{-1}=\frac{1}{2\pi i}\oint\limits_{C}f(w) dw=0,
$$
$$
a_{-2}=\frac{1}{2\pi i}\oint\limits_{C}f(w) (w-z_0) dw=0,
$$
$$
a_{-3}=\frac{1}{2\pi i}\oint\limits_{C}f(w) (w-z_0)^{2}dw,
$$
e assim por diante, já que os integrandos são analíticos.
Definição: Dizemos que uma função \(g(z)\) é analítica (ou regular) em \(z=\infty\) se \(g( 1/w)\) for analítica em \(w=0\). Neste caso vale a expansão
$$
g\left( \frac{1}{w} \right) =b_0+b_{1}w+b_{2}w^{2}+\ldots
$$
na vizinhança de \(w=0\), ou, equivalentemente,
$$
g(z) =b_0+\frac{b_{1}}{z}+\frac{b_{2}}{w^{2}}+\ldots.
$$
Se \(f\) uma função analítica no ponto \(z_0\) ela possui expansão de Taylor dada por
$$
f(z) =\sum\limits_{n=0}^{\infty }a_{n}(z-z_0)^{n},\ \text{na vizinhança }\left\vert z-z_0\right\vert \lt r.
$$
Observe que se \(a_0=0\) temos que \(z_0\) é um zero de \(f\), enquanto se \(a_{n}=0\), para todo \(n\), então a função é identicamente nula \(f\equiv 0\) na vizinhança de \(z_{0.}\) Excluindo-se este último caso, suponha que \(a_{m}\), é o primeiro coeficiente não nulo na expansão de Taylor. Neste caso
$$
f(z) =\sum\limits_{n=m}^{\infty }a_{n}(z-z_0)^{n}=a_{m}(z-z_0)^{m}+a_{m+1}(z-z_0)^{m+1}+\ldots
$$
e dizemos que \(z_0\) é um zero de ordem \(m\) da função. O teorema seguinte fornece um critério de determinação de zeros de uma função.
Teorema: \(z_0\) é um zero de ordem \(m\) de uma função analítica \(f\) se, e somente se, existe uma função \(g\) satisfazendo
$$
f(z) =(z-z_0)^{m}g(z) \; \text{ onde } \; g( z_0) \neq 0.
$$
Alternativamente, o limite
$$
\lim_{z\rightarrow z_0}\frac{f(z) }{(z-z_0)^{m}}
$$
é finito e não nulo.
Demonstração: Fatorando \((z-z_0)^{m}\) na expressão (9) acima obtemos
$$
f(z) =(z-z_0)^{m}\left[ a_{m}+a_{m+1}(z-z_0) +a_{m+2}(z-z_0)^{2}+\ldots \right]
$$
$$
=(z-z_0)^{m}\sum\limits_{n=0}^{\infty }a_{m+n}(z-z_0)^{n}.
$$
Denotando \(g(z) =\sum\nolimits_{n=0}^{\infty }a_{m+n}(z-z_0)^{n}\) temos que, se \(z_0\) é zero de ordem \(m\) de \(f\) então
$$
f(z) =(z-z_0)^{m}g(z) \; \text{ onde } \; g( z_0) \neq 0.
$$
Observamos que
$$
\lim_{z\rightarrow z_0}\frac{f(z) }{(z-z_0)^{m}}=g( z_0) =a_{m}.
$$
Se \(f\) é regular (analítica) em \(z=\infty\) este ponto é chamado um zero de ordem \(m\) se \(w=0\) é zero de ordem \(m\) de \(f(1/w)\).
Exercícios :
1. Encontre as séries de Laurent nas regiões dadas:
a. \(f(z) =\frac{1+z}{z},\; z_0=0,\;\;0 \lt \left\vert z \right\vert \lt \infty\).
b. \(f(z) =\frac{z}{z^{2}+1},\; z_0=0,\;\;0 \lt \left\vert z \right\vert \lt \infty\).
c. \(f(z) =\frac{1}{(z-i)(z-2)}, \; z_0=2, \; 0 \lt \left\vert z-2 \right\vert \lt \sqrt{5}\).
d. \(f(z) =\frac{z^{5}}{z-1},\; z_0=0,\;\; \left\vert z \right\vert \gt 1\).
e. \(f(z) =z^{5}\text{ e}^{1/z},\; z_0=0,\;\;\left\vert z \right\vert \gt 0\).
f. \(f(z) =\frac{\text{sen }z}{( z-\pi )^{3}},\; z_0=\pi , \;\; z\neq \pi\).
2. Seja \(f\) uma função analítica no ponto \(z_0\). Mostre que \(z_0\) é um zero de ordem \(m\) de \(f\) se, e somente se,
$$
f(z_0)=0,\; f'(z_0) =0,\ldots ,\; f^{(m-1)}(z_0) =0 \; \text{ e }\; f^{(m)}(z_0) \neq 0.
$$
3. Determine a ordem do zero \(z=0\;\;\) nas seguintes funções:
$$
\begin{array}{ll}
\text{a.}\;\; (\cos z-1)^{3}\text{sen }z,\;\;
& \text{b.}\;\; \frac{(1-\cos z) \text{ sen }^{2}z}{1-\text{e}^z},\;\;
& \text{c.}\;\; (\text{ e}^{z}-1-z)^{3}\text{sen }^{2}z,\;\;
\\
\text{d.}\;\; \text{e}^{\text{sen }z}-\text{ e}^{z},\;\;
& \text{e.}\;\; (\text{e}^{z^{2}}-1)(\text{sen }^{2}z-z^{2}),\;\;
& \text{f.}\;\; \text{e}^{\text{sen }z}-\text{e}^{\tan z}.
\end{array}
$$
Algumas respostas e sugestões:
1a. A função já está sob a forma de uma série de Laurent: \(f(z) =1+1/z.\)
b. Escreva sob a forma de frações parciais \(f(z)=\frac{A}{z+i}+\frac{B}{z-i}\) para achar
$$
f(z) =\frac{1}{2}( z-i)^{-1}+\sum\limits_{n=0}^{\infty }\frac{(-1)^{n+1}(z-i)^{n}}{(2i)^{n+1}}.
$$
Um arco contínuo é o conjunto parametrizado
$$
C=\left\{ z\left( t\right) =x\left( t\right) +iy\left( t\right) ;\;a\leq t\leq b\right\} ,
$$
onde \(z\left( t\right)\) é contínua. Observamos que \(z\left(t\right)\) é contínua se, e somente se, \(x(t)\), e \(y(t)\) são contínuas. O mesmo arco, com orientação oposta é denotado por \(-C\) e pode ser parametrizado por
$$
z_{1}\left( t\right) =z\left( -t\right) ,\;-b\leq t\leq -a.
$$

Um arco simples ou arco de Jordan é um arco sem auto-interseções. Uma curva fechada é aquela que satisfaz \(z\left( t_{1}\right) =z\left( t_{2}\right)\), com \(t_1 \neq t_2\). Na figura 2 as curvas são: (a) simples, (b) não simples, com interseção, (c) fechada simples, também chamada curva de Jordan, (d) fechada, com auto-interseção.

Um arco \(C\), parametrizado por \(z\left( t\right) =x\left( t\right) +iy\left(t\right)\) é dito regular se a derivada \(z^{\prime }\left( t\right)=x^{\prime }\left( t\right) +iy^{\prime }\left( t\right)\) existe, é contínua e \(z^{\prime }\left( t\right) \neq 0\), \(\forall t\) no intervalo de definição da curva. Isto garante que a curva possui tangente em qualquer um de seus pontos. O ângulo formado pela tangente com o eixo \(\mathcal{O}x\) é \(\arg \left( z^{\prime }\right)\).
Um contorno ou caminho é um arco regular por partes, ou seja, um arco composto por sub-arcos regulares, \(C=C_{1}\cup C_{2}\cup \ldots \cup \;C_{n}\).
Exercício Resolvido: Faça um esboço das curvas parametrizadas por
$$
\left.
\begin{array}{lll}
\text{(a)}\;\; z_{1}=1+it, & & \text{(b)}\;\; z_{2}=t+it, \\
\text{(c)}\;\; z_{3}=t^{2}+it, & & \text{(d)}\;\; z_{4}=t+it^{2},
\end{array}
\right\} \;\;\; \text{ todas no intervalo } 0 \leq t\leq 1.
$$
A curva (a) tem parte real constante \(x=1\) e imaginária \(y=t\). Ela é, portanto, o segmento de reta \(\left( 1,t\right)\) no plano complexo, com início em \(\left( 1,0\right)\) e fim em \(\left( 1,1\right)\). A curva (b) corresponde a \(x=t,\;y=t\) ou, em outra representação, o segmento de reta \(y=x\). A curva (c) é o arco de parábola \(x=y^{2}\) enquanto a curva (d) é o arco de parábola \(y=x^{2}\), como representado na figura 3(a).

Exercício Resolvido: Identifique e faça um esboço da curva parametrizada por \(z\left( t\right) =re^{i\theta };\;0\leq\theta \leq 2\pi\).
Esta curva pode ser escrita como \(z\left( \theta \right) =r\left( \cos \theta +i\text{sen }\theta \right)\) e portanto tem partes real e imaginária
$$
x=r\cos \theta ,\ \ y=r\text{sen }\theta .
$$
Observe que \(x^{2}+y^{2}=r^{2}\) para qualquer valor de \(\theta\). Quando o parâmetro varia de \(0\) até \(2\pi\) a curva realiza uma volta completa sobre a circunferência de centro na origem e raio \(r\). Esta é uma curva de Jordan, representada na figura 3(b).
Teorema de Jordan: Toda curva \(C\) fechada simples divide o plano em duas regiões, sendo \(C\) sua fronteira comum. O interior \(R\) é uma região limitada, simplesmente conexa, ou seja, qualquer curva fechada simples em seu interior pode ser deformada continuamente sem sair de \(R\).

Como exemplo, o domínio da função \(f\left( z\right) =\ln z\) é
$$
D\left[ \ln \left( z\right) \right] =\mathbb{C}-\left\{ 0\right\} =\left\{ z\in \mathbb{C};\ z\neq 0\right\}
$$

e é uma região perfurada, conexa mas não simplesmente conexa, a que chamaremos região multiplamente conexa.
Exercícios:
Identifique as curvas dadas abaixo:
1. \(z=3t+it^{2}, -\infty \lt t \lt \infty\),
2. \(z=3t^{2}+5it, -\infty \lt t \lt \infty\),
3. \(z=r\left( \cos t+i\text{sen }t\right),\; -\pi /4\lt t \lt \pi ,\; r\gt 0\),
4. \(z=1/t+it, 1\lt t \lt \infty\),
5. \(z=t+2i/t, -\infty \lt t \lt 0\),
6. \(z=t+i\sqrt{1-t^{2}}, -1\lt t \lt 1\),
7. \(\left\vert z-2i\right\vert =2\).
8. Qual é a equação da reta em \(\mathbb{C}\) que liga os pontos \(0\) até \(1+i\,\)?
9. Qual é a equação da reta que liga os pontos \(1+i\) até \(0\)?
10. Qual é a equação da reta que liga os pontos \(z_{1}=1+2i\) a \(z_{2}=2+5i\)?
11. Qual é a equação da circunferência com centro em \(z_0=i\) e raio \(r=1\)?
Seja \(F\left( t\right) =U\left( t\right) +iV\left( t\right)\) uma função contínua no intervalo \(\left[ a,b\right]\). Sua integral é definida por
$$
\int_{a}^{b}F\left( t\right) dt=\int_{a}^{b}U\left( t\right)dt+i\int_{a}^{b}V\left( t\right) dt.
$$
Seguem da definição as seguintes propriedades: suas partes real e imaginária são, respectivamente
$$
\text{Re}\int_{a}^{b}F\left( t\right) dt=\int_{a}^{b}U\left( t\right)dt=\int_{a}^{b}\text{Re}\left[ F\left( t\right) \right] dt,
$$
$$
\text{Im}\int_{a}^{b}F\left( t\right) dt=\int_{a}^{b}V\left( t\right) dt=\int_{a}^{b}\text{Im}\left[ F\left( t\right) \right] dt.
$$
A integral é linear,
$$
\int_{a}^{b}\left[ F\left( t\right) +G\left( t\right) \right]\,dt=\int_{a}^{b}F\left( t\right) dt+\int_{a}^{b}G\left( t\right) dt,
$$
$$
\int_{a}^{b}\alpha F\left( t\right) \,dt=\alpha \int_{a}^{b}F\left( t\right)
dt.
$$
Além disto, uma propriedade que será bastante útil é a chamada desigualdade triangular,
$$
\left\vert \int_{a}^{b}F\left( t\right) \,dt\right\vert \leq \int_{a}^{b}\left\vert F\left( t\right) \right\vert \,dt.
$$
Exercício Resolvido: Demonstre a desigualdade triangular, propriedade (3).
Observamos primeiro que \(\int_{a}^{b}F\left( t\right) \,dt\) é um número complexo e o escrevemos em sua forma polar
$$
\int_{a}^{b}F\left( t\right) \,dt=re^{i\theta },\;\;\text{ onde }r=\left\vert \int_{a}^{b}F\left( t\right) \,dt\right\vert .
$$
Multiplicamos os dois lados da última equação por \(e^{-i\theta }\) para obter
$$
r=e^{-i\theta }\int_{a}^{b}F\left( t\right) \,dt=\int_{a}^{b}e^{-i\theta} F\left( t\right) \,dt.
$$
Como \(r\) é real, \(r=\text{Re}\left\{ r\right\}\) ou seja
$$
r=\text{Re}\int_{a}^{b}e^{-i\theta }F\left( t\right) \,dt=\int_{a}^{b}\text{Re}\left[ e^{-i\theta }F\left( t\right) \right] \,dt,
$$
onde se aplicou a propriedade (3). Considerando que, para qualquer complexo, vale a relação \(\text{Re}\left\{ z\right\} \leq \left\vert z\right\vert\) então o integrando é \(\text{Re}\left[ e^{-i\theta}F\left( t\right) \right] \leq \left\vert e^{-i\theta }F\left( t\right) \right\vert =\left\vert F\left( t\right) \right\vert\) para todo \(t\), lembrando que a última igualdade vale porque \(e^{-i\theta }\) é um complexo com valor absoluto igual a um. Concluimos que
$$
\left\vert \int_{a}^{b}F\left( t\right) \,dt\right\vert =r\leq \int_{a}^{b}\left\vert F\left( t\right) \,\right\vert \,dt.
$$
Fica assim mostrada a propriedade.
Definimos a integral de contorno, ou integral curvilínea, \(\int_{C}f\left( z\right) \,dz\) onde \(C\) é um caminho qualquer e \(f=u+iv\) é uma função contínua em \(a\leq t\leq b\) como
$$
\int_{C}f\left( z\right) \,dz=\int_{a}^{b}f\left( z\left( t\right) \right)z^{\prime }\left( t\right) dt.
$$
Observe que \(f\left( z\right)\) pode ser definida para qualquer ponto do plano complexo mas, na avaliação da integral, somente são considerados seus valores sobre a curva \(C\). Estas integrais são avaliadas da seguinte forma: descrevemos o caminho \(C\) por meio de alguma parametrização \(z\left( t\right) =x\left( t\right) +iy\left(t\right)\), encontramos a diferencial,
$$
dz=\left[ x^{\prime }\left( t\right) +iy^{\prime }\left( t\right) \right] dt
$$
e os valores da função sobre este caminho transformando a integral de caminho em uma integral definida complexa, definida na seção anterior que, por sua vez, se reduz a duas integrais definidas ordinárias. Se \(f=u+iv\) então
$$
\int_{C}f\left( z\right) \,dz=\int_{a}^{b}\left( u+iv\right) \left(
x^{\prime }+iy^{\prime }\right) dt=\int_{a}^{b}\left[ \left( ux^{\prime
}-vy^{\prime }\right) +i\left( u\,y^{\prime }+vx^{\prime }\right) \right] dt.
$$
Lembramos que o contorno deve ser composto por um número finito de arcos regulares, onde \(z^{\prime }\neq 0\).
Exemplo 1: Calcule a integral de contorno
$$
I=\int\limits_{C}f\left( z\right) dz \;\; \text{ onde } \;\; f\left( z\right)=2x-y+ix^{2},
$$
e \(C\) é o segmento de reta ligando os pontos \(0\) a \(1+i\). O primeiro passo é parametrizar este segmento. Ele pode ser descrito como
$$
C: z=\left( 1+i\right) t,\; \; 0\leq t\leq 1.
$$
Sobre este segmento \(x=t\) e \(y=t\) e, portanto \(f\left( z\right)=2t-t+it^{2},\) enquanto \(dz=z^{\prime }dt=\left( 1+i\right) dt\). A integral é
$$
I=\left( 1+i\right) \int_{0}^{1}\left( t+it^{2}\right) dt=\left( 1+i\right)\left. \left( \frac{t^{2}}{2}+i\frac{t^{3}}{3}\right) \right\vert _{0}^{1}
=\frac{1}{6}\left( 1+5i\right).
$$
Exemplo 2: Vamos calcular a integral de contorno
$$
I=\int\limits_{C}f\left( z\right) dz \text{ onde }f\left( z\right)=\left\vert z\right\vert
\;\;\;\;\text{ e }\;\;\;\; C=\left\{ z=re^{i\theta }, 0\leq \theta \leq \pi ,\; r\; \text{ constante }\right\}.
$$
Note que \(C\) é o arco da circunferência de raio \(r\) no primeiro e segundo quadrantes. Sobre \(C\), \(f\left( z\right) =\left\vert z\right\vert =r\). Como \(r\) é constante é conveniente parametrizar o caminho usando a variável \(\theta\), fazendo
$$
z\left( \theta \right) =r\left( \cos \theta +i\text{sen }\theta \right) ,\; \; 0\leq \theta \leq \pi,
$$
enquanto a diferencial é
$$
dz=z^{\prime }d\theta =r\left( -\text{sen }\theta +i\cos \theta \right) d\theta.
$$
Juntando os termos a integral procurada é
$$
I=\int_{0}^{\pi }r^{2}\left( -\text{sen }\theta +i\cos \theta \right) d\theta=r^{2}\left[ \left. \cos \theta \right\vert _{0}^{\pi }+i\left. \text{sen }
\theta \right\vert _{0}^{\pi }\right] =-2r^{2}.
$$
Observe que, se o caminho fosse fechado, \(z=re^{i\theta },\; 0\leq \theta \leq 2\pi\), a integral seria nula pois
$$
I=\int_{0}^{2\pi }r\left( ire^{i\theta }\right) d\theta =ir^{2}\int_{0}^{2\pi }e^{i\theta }d\theta =0.
$$
Para calcular a integral neste segundo caso usamos a parametrização \(z=re^{i\theta }\), \(0\leq \theta \leq 2\pi\), com a respectiva diferencial \(dz=ire^{i\theta }d\theta\).
As seguintes propriedades valem para a integral de contorno:
i) A integral de contorno é linear:
$$
\int_{C}\left[ f\left( z\right) \,+g\left( z\right) \right]
\,dz=\int_{C}f\left( z\right) \,dz+\int_{C}g\left( z\right) \,dz
$$
$$
\int_{C}\alpha f\left( z\right) \,dz=\alpha \int_{C}f\left( z\right) \,dz,
$$
onde \(\alpha\) é uma constante complexa.
ii) Se \(C\) é a união de caminhos disjuntos, \(C=C_{1}\cup C_{2}\cup \ldots \cup C_{r}\) então
$$
\int_{C}f\left( z\right) \,dz=\int_{C_{1}}f\left( z\right) \,dz+\int_{C_{2}}f\left( z\right) \,dz+\ldots +\int_{C_{r}}f\left( z\right) \,dz.
$$
Segue daí que a integral ao longo de um caminho fechado não depende do ponto inicial onde se inicia o caminho. Dizemos que ela é invariante
por translações do parâmetro.
iii) A integral muda de sinal se percorremos o caminho em sentido oposto:
$$
\int_{-C}f\left( z\right) \,dz=-\int_{C}f\left( z\right) \,dz.
$$
Para mostrar esta afirmação fazemos
$$
-C=\left\{ z_{1}\left( t\right) =z\left( -t\right) ;\;-b\leq t\leq -a\right\}
$$
e, portanto,
$$
I=\int_{-C}f\left( z\right) \,dz=\int_{-b}^{-a}f\left( z_{1}\left( t\right) \right) z_{1}^{\prime }\left( t\right) dt.
$$
Como \(z_{1}\left( t\right) =z\left( -t\right)\) temos que
$$
I=\int_{-b}^{-a}f\left( z\left( -t\right) \right) \frac{dz\left( -t\right) }{dt}dt.
$$
Fazendo a mudança de variáveis \(\tau =-t\) temos
$$
dt=-d\tau \;\;\; \text{ e }\;\;\; \frac{d}{dt}=\frac{d}{d\tau }\frac{d\tau }{dt}=-\frac{d}{d\tau }
$$
e a integral pode ser escrita como
$$
I=\int_{b}^{a}f\left( z\left( \tau \right) \right) \,\frac{dz\left( \tau
\right) }{d\tau }\,d\tau =-\int_{a}^{b}f\left( z\left( \tau \right) \right)
dz=-\int_{C}f\left( z\right) \,dz.
$$
iv) Vale a desigualdade
$$
\left\vert \int_{C}f\left( z\right) \,dz\right\vert \leq \int_{C}\left\vert
f\left( z\right) \right\vert \,\left\vert dz\right\vert ,
$$
que é decorrente da propriedade semelhante válida para \(\int_{a}^{b}F\left( t\right) \,dt\), propriedade (3).
v) Se \(f\) é uma função contínua sobre o arco \(C\) então existe uma constante \(M\) positiva tal que \(\left\vert f\left( z\right) \right\vert \leq M,\;\forall z\in C\). Daí, e da propriedade anterior,
$$
\left\vert \int_{C}f\left( z\right) \,dz\right\vert \leq \int_{C}\left\vert
f\left( z\right) \right\vert \,\left\vert dz\right\vert \leq
M\int_{C}\left\vert dz\right\vert =ML,
$$
onde \(L\) é o comprimento do arco \(C\). A última igualdade pode ser justificada da seguinte forma: se \(z\left( t\right) =x\left( t\right) +iy\left( t\right)\) então \(dz=dx+idy\) e
$$
\int_{C}\left\vert dz\right\vert =\int_{a}^{b}\sqrt{dx^{2}+dy^{2}}
=\int_{a}^{b}\sqrt{\left( \frac{dx}{dt}\right) ^{2}+\left( \frac{dy}{dt}
\right) ^{2}}dt=L.
$$
vi) A integral \(\int_{C}f\left( z\right) \,dz\) não depende da escolha de uma parametrização para \(C\).
Representando o caminho \(C\) por meio da parametrização \(z\left(t\right)\), \(t_{1}\leq t\leq t_{2}\) então calculamos
$$
I=\int_{C}f\left( z\right) \,dz=\int_{t_{1}}^{t_{2}}f\left( z\left( t\right)\right) z^{\prime }\left( t\right) dt.
$$
Podemos também usar outra parametrização dada por \(z_{1}\left(\tau \right) =z\left( t\left( \tau \right) \right)\), \(\tau _{1}\leq \tau
\leq \tau _{2}\) onde \(t\left( \tau \right)\) é uma função crescente e monótona, \(t_{1}=t\left( \tau _{1}\right) ,\;t_{2}=t\left(
\tau _{2}\right)\). Neste caso
$$
I=\int_{C}f\left( z\right) \,dz=\int_{\tau _{1}}^{\tau _{2}}f\left(
z_{1}\left( \tau \right) \right) z^{\prime }\left( \tau \right) d\tau .
$$
Mas
$$
\frac{d\left( z_{1}\left( \tau \right) \right) }{d\tau }=\frac{d\left(
z\right) }{dt}\frac{dt}{d\tau }
$$
portanto
$$
I=\int_{\tau _{1}}^{\tau _{2}}f\left( z_{1}\left( \tau \right) \right) \frac{
d\left( z_{1}\left( \tau \right) \right) }{d\tau }d\tau =\int_{\tau
_{1}}^{\tau _{2}}f\left( z\left( t\left( \tau \right) \right) \right) \frac{
dz}{dt}\frac{dt}{d\tau }d\tau =\int_{t_{1}}^{t_{2}}f\left( z\left( t\right)
\right) \frac{dz}{dt}dt.
$$
Qualquer parametrização encontrada para a curva \(C\) pode ser usada na avaliação da integral, desde que o sentido seja preservado. Dizemos que a integral é invariante sob reparametrizações do caminho \(C\).
Exercício Resolvido: Calcule \(I=\int_{C}f\left(z\right) \,dz\) onde \(f\left( z\right) =z\) e \(C\) é um caminho qualquer ligando \(z_{1}\) a \(z_{2}\).
Vamos representar o caminho \(C\) por
$$
C=\left\{ z\left( t\right) =x\left( t\right) +iy\left( t\right) ;\;a\leq
t\leq b\right\} ,\;z\left( a\right) =z_{1},\;z\left( b\right) =z_{2}.
$$
Então \(dz=dx+idy=\left( x^{\prime }+iy^{\prime }\right) dt\) e a integral procurada é
$$
I=\int_{a}^{b}z\left( t\right) z^{\prime }\left( t\right)
\,dt=\int_{a}^{b}\left( x+iy\right) \left( x^{\prime }+iy^{\prime }\right)
dt=
$$
$$
=\int_{a}^{b}\left( x+iy\right) \left( x^{\prime }+iy^{\prime }\right)
dt=\int_{a}^{b}\left[ \left( xx^{\prime }-yy^{\prime }\right) +i\left(
xy^{\prime }+yx^{\prime }\right) \right] dt.
$$
Observamos agora que o integrando é uma diferencial exata:
$$
\frac{d}{dt}\left( x^{2}-y^{2}+2ixy\right) =2\left[ \left( xx^{\prime
}-yy^{\prime }\right) +i\left( xy^{\prime }+yx^{\prime }\right) \right] ,
$$
portanto
$$
I=\frac{1}{2}\int_{a}^{b}\frac{d}{dt}\left( x^{2}-y^{2}+2ixy\right) dt=\frac{
1}{2}\left. \left( x^{2}-y^{2}+2ixy\right) \right\vert _{a}^{b}=
$$
$$
\frac{1}{2}\left. z^{2}\right\vert _{a}^{b}=\frac{1}{2}\left[ z^{2}\left(
b\right) -z^{2}\left( a\right) \right] =\frac{1}{2}\left[ z_{2}^{2}-z_{1}^{2}
\right] .
$$
Aproveitamos este exercício para indicar um resultado importante, que será estudado na próxima seção. Se o caminho \(C\) é fechado então \(z\left( a\right) =z\left( b\right)\) e esta integral, sobre o caminho fechado, é nula:
$$
\int_{C}z\,dz\equiv \oint z\,dz=0.
$$
O sinal \(\oint\) indica integração sobre um caminho fechado. Como veremos este resultado não é uma coincidência, mas faz parte de um resultado mais geral que será expresso pelo teorema de Cauchy, descrito na próxima seção.
Exercícios :
1. Dados os pontos \(a=\left( 1,~0\right)\), \(b=\left( 0,~m\right), c=\left( 1,~m\right)\), calcule \(\int\limits_{C}f\left( z\right) dz\) onde \(f\left( z\right) =\bar{z}\) e \(C\) é o caminho que liga a origem ao ponto \(c\) ao longos de três percursos: \(\mathcal{O}c,\; \mathcal{O}ac \;\) e \(\mathcal{O}bc\).
2. Calcule \(\int\limits_{C}f\left( z\right)dz\) onde:
a. \( f\left( z\right) =\left\vert z\right\vert ; C=\left \{ z=re^{i\theta},\; \pi /2\leq \theta \leq \pi \right\}\)
b. \(f\left( z\right) =z^{2};\; C=\left\{ z=re^{i\theta },\; 0\leq \theta \leq \pi \right\}\)
c. \(f\left( z\right) =z^{2}; C=\left\{ z=re^{i\theta },\ -\pi \leq \theta \leq \pi \right\}\)
d. \(f\left( z\right) =\sqrt{z}; C=\left\{ z=re^{i\theta },\ 0\leq \theta \leq 2\pi \right\}\)
e. \(f\left( z\right) =\sqrt{z}; C=\left\{ z=re^{i\theta },\ -\pi \leq \theta \leq \pi \right\}\)
f. \(f\left( z\right) =\left\vert z\right\vert\), ao longo do segmento de reta de zero até \(-2+3i\).
g. \(f\left( z\right) =x^{2}-y^{2}+i\left( x-y^{2}\right)\), ao longo do segmento de reta de zero até \(3+2i\).
h. \(f\left( z\right) =y-x^{2}\), ao longo dos caminhos \(\mathcal{O}ac\) e \(\mathcal{O}bc\), onde \(\mathcal{O=}\left( 0, 0\right) , a=\left(2, 0\right) , b=\left( 0, 1\right)\) e \(c=\left( 2, 1\right)\).
3. Se \(C\) é um caminho qualquer ligando os pontos \(z_{1}\) a \(z_{2}\) mostre que \(\int_{C}dz= z_{2}-z_{1}\).
Algumas soluções:
1) \(\int_{\mathcal{O}c}=\frac{1+m^{2}}{2},\; \int_{\mathcal{O}ac}=\frac{1}{2}\left( 1+m^{2}+im\right) ,\; \int_{\mathcal{O}bc}=\frac{1}{2} \left(
1+m^{2}-2im\right)\). As integrais podem ser calculadas da seguinte forma: Representamos graficamente os três caminhos na figura 4 e buscamos uma parametrização para cada um deles.

O caminho direto \(\mathcal{O}c\) é a reta \(\left\{ z\left( t\right) =\left(1+im\right) t,\ 0\leq t\leq 1\right\}\). Sua diferencial é \( dz=z^{\prime }dt=\left( 1+im\right) dt\), enquanto o integrando é \(\bar{z}=\left( 1-im\right) t\). A integral pode ser avaliada como
$$
I_{1}=\int_{\mathcal{O}c}\bar{z}dz=\int_{0}^{1}\left(1-im\right) t\left(1+im\right) dt=\left( 1+m^{2}\right) \int_{0}^{1}tdt=\frac{1+m^{2}}{2}.
$$
ii) O caminho \(\mathcal{O}ac\) é a união de dois arcos simples,
$$
\mathcal{O}ac=\left\{ z\left( t\right) =t,\ 0\leq t\leq 1\right\} \cup \left\{ z\left( t\right) =1+imt,\ 0\leq t\leq 1\right\}.
$$
As diferenciais são, respectivamente, \(dz=dt\) e \(dz=imdt\) sobre cada parte do caminho. A integral pode ser partida em dois pedaços, \(\int_{\mathcal{O}ac}=\int_{\mathcal{O}a}+\int_{ac}\), ou seja
$$
I_{2}=\int_{0}^{1}tdt+\int_{0}^{1}\left( 1-imt\right) imdt=\int_{0}^{1}tdt+im\int_{0}^{1}dt+m^{2}\int_{0}^{1}tdt=\frac{1}{2}\left(1+m^{2}+2im\right).
$$
iii) O caminho \(\mathcal{O}bc\) é a união dos arcos
$$
\mathcal{O}bc=\left\{ z\left( t\right) =imt,\ 0\leq t\leq 1\right\} \cup \left\{ z\left( t\right) =t+im,\ 0\leq t\leq 1\right\}.
$$
As diferenciais são \(dz=imdt\) e \(dz=dt\) sobre cada parte do caminho e a integral pode ser avaliada como
$$
I_{3}=\int_{\mathcal{O}bc}=\int_{0}^{1}\left( -imt\right)imdt+\int_{0}^{1}\left( t-im\right)dt =
$$
$$
=m^{2}\int_{0}^{1}tdt+\int_{0}^{1}tdt-im\int_{0}^{1}tdt=\frac{1}{2}\left(1+m^{2}-2im\right).
$$
Observamos que o valor da integral é diferente para cada caminho tomado, neste caso.
$$
\begin{array}{rll}
\text{2a. }\; \left(i-1\right) r^{2}\;\; & \text{b. }\; -2r^{3}/3 \;\; & \text{c. }\; \text{zero} \\
\text{d. }\; -4r\sqrt{r}/3 \;\; & \text{e. }\; 4r\sqrt{r}/3i \;\; & \text{f. }\; \sqrt{13}\left(3i-2\right) /2
\end{array}
$$
O seguinte teorema foi originalmente foi apresentada por Cauchy no início da década de 1800, afirmando que a integral de uma função analítica, realizada sobre um contorno fechado, é sempre nula.
Antes de enunciar o teorema de Cauchy vamos definir o sentido orientação de um contorno e fazer uma breve revisão sobre o teorema de Green.
Definição. Dizemos que o contorno fechado \(C\) é positivamente orientado se um observador com trajetória sobre \(C\) deixa sempre a região interior envolvida por \(C\) à sua esquerda.

Teorema de Green1: Sejam \(P\left( x,y\right)\) e \(Q\left( x,y\right)\) duas funções definidas em uma região \(R\) simplesmente conexa, com derivadas primeiras contínuas. Então, para qualquer contorno fechado simples \(C\) contido em \(R\), vale
$$
\iint_{R^{\prime }}\left( \frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\right) dxdy=\oint_{C}Pdx+Qdy,
$$
onde \(R^{\prime }\) é a região interior a \(C\). Uma notação útil pode ser utilizada escrevendo-se \(\vec{t}=\left(t_{x},\,t_{y}\right)\), para um vetor tangente ao contorno \(C\), e \(\vec{n} =\left( n_{x},\,n_{y}\right)\) um vetor unitário normal à \(C\). Então
$$
\left( dx,\,dy\right) =\vec{t}ds,\;\left( dy,\;-dx\right) =\vec{n}ds.
$$
Definindo um vetor \(F=\left( Q,\,-P\right)\) podemos escrever a equação (4) como
$$
\iint_{R^{\prime }}\text{div}\vec{F}\,dxdy=\oint_{C}\vec{F}\cdot \vec{n}\,ds.
$$
Teorema de Cauchy: Seja \(f\) uma função analítica em uma região simplesmente conexa \(R\). Então
$$
\oint_{C}f\left( z\right) \,dz=0,
$$
onde \(C\) é qualquer caminho fechado em \(R\). Equivalentemente, a integral
$$
\int_{z_{1}}^{z_{2}}f\left( z\right) \,dz
$$
não depende da escolha do caminho tomado mas apenas dos pontos extremos.
Demonstração: Fazemos \(f=u+iv\) e\(\;z=x+iy\). Então
$$
I=\oint_{C}f\left( z\right) \,dz=\oint_{C}\left( u+iv\right) \left(dx+idy\right) =
$$
$$
\oint_{C}\left( udx-vdy\right) +i\oint_{C}\left( udy+vdx\right).
$$
Usamos agora o teorema de Green, equação (4), para tansformar estas integrais em
$$
I=-\iint_{R^{\prime }}\left( \frac{\partial v}{\partial x}+\frac{\partial u}{\partial y}\right) dxdy+i\iint_{R^{\prime }}\left( \frac{\partial u}{
\partial x}-\frac{\partial v}{\partial y}\right) dxdy=0.
$$
Notamos que as integrais acima são nulas devido às condições de Cauchy-Riemann, \(u_{x}=v_{y}\) e \(v_{x}=-u_{y}\), válidas para funções analíticas. A equivalência dos enunciados pode ser mostrada das seguinte forma: construímos dois caminhos \(C_{1}\) e \(C_{2}\) ligando os pontos \(z_{1}\) e \(z_{2}\) e supomos que as integrais sobre os caminhos são iguais, \(\int_{C_1}=\int_{C_{2}}\). A integral avaliada sobre o caminho fechado \(C_{1}\cup \left(-C_{2}\right)\) é nula,
$$
\oint_{C}f\left( z\right) \,dz=\int_{C_{1}}f\left( z\right)\,dz-\int_{C_{2}}f\left( z\right) \,dz=0,
$$
já que a integração não depende do caminho escolhido. Por outro lado, se a integral fechada é nula concluímos que a integração não depende do caminho pois
$$
0=\oint_{C}=\int_{C_{1}}-\int_{C_{2}}\Rightarrow \int_{C_{1}}=\int_{C_{2}}.
$$
O teorema de Cauchy, também conhecido como teorema de Cauchy-Goursat, é o teorema fundamental da teoria das funções analíticas. Os principais resultados que ainda estudaremos são consequência direta deste teorema. Em particular veremos que funções analíticas possuem derivadas de todas as ordens e estas derivadas são contínuas. Nesta seção mostraremos que uma função analítica possue uma primitiva2.
Teorema: Seja \(f\) uma função analítica em uma região \(R\) simplesmente conexa. Então a forma geral de sua primitiva é
$$
F\left( z\right) =\int_{z_0}^{z}f\left( w\right) dw+c,
$$
onde \(c\) é uma constante arbitrária, \(z_0\) é um ponto fixo qualquer de \(R\) e a integração é feita ao longo de um contorno inteiramente contido em \(R\). Além disto a função \(F\left( z\right)\) definida desta forma é analítica.
Demonstração: A função \(F\left( z\right)\) está bem definida uma vez que a integral não depende do caminho escolhido. Sua derivada, por definição, é
$$
F^{\prime }\left( z\right) =\lim_{h\rightarrow 0}\frac{1}{h}\left[ F\left(z+h\right) -F\left( z\right) \right].
$$
Note que
$$
F\left( z+h\right) -F\left( z\right) =\left(
\int_{z_0}^{z+h}-\int_{z_0}^{z}\right) f\left( w\right)
dw=\int_{z}^{z+h}f\left( w\right) dw.
$$
Definindo uma função auxiliar \(\eta \left( z,w\right) =f\left(w\right) -f\left( z\right)\) podemos escrever
$$
F^{\prime }\left( z\right) =\lim_{h\rightarrow 0}\frac{1}{h}\int_{z}^{z+h}
\left[ f\left( z\right) +\eta \left( z,w\right) \right] dw=f\left( z\right)
+\lim_{h\rightarrow 0}\frac{1}{h}\int_{z}^{z+h}\eta \left( z,w\right) dw.
$$
Na relação acima foi usado o seguinte fato:
$$
\lim_{h\rightarrow 0}\frac{1}{h}\int_{z}^{z+h}dw=1.
$$
Resta mostrar que o limite no segundo termo, é nulo. Para isto observe que, em módulo, vale
$$
\left\vert \frac{1}{h}\int_{z}^{z+h}\eta \left( z,w\right) dw\right\vert \leq \frac{1}{\left\vert h\right\vert }\int_{z}^{z+h}\left\vert \eta \left(
z,w\right) \right\vert \left\vert dw\right\vert.
$$
Como \(f\left( z\right)\) é analítica, portanto contínua, dado \(\varepsilon \gt 0\;\) existe \(\;\delta \gt 0\;\) tal que
$$
\left\vert \eta \left( z,w\right) \right\vert =\left\vert f\left( w\right)-f\left( z\right) \right\vert \gt \varepsilon \;\text{ para }\;\left\vert
w-z\right\vert \gt \delta.
$$
Portanto
$$
\left\vert \frac{1}{h}\int_{z}^{z+h}\eta \left( z,w\right) dw\right\vert \lt \frac{\varepsilon }{\left\vert h\right\vert }\int_{z}^{z+h}\left\vert
dw\right\vert =\varepsilon.
$$
No limite \(h \rightarrow 0\) temos que \(\varepsilon \rightarrow 0\) de onde concluímos, como pretendíamos, que \(F’=f\).
Corolário: Nas mesmas condições do teorema acima temos que
$$
\int_{z_0}^{z_{1}}f\left( z\right) dz=F\left( z_{1}\right) -F\left(z_0\right),
$$
onde \(F\left( z\right)\) é uma primitiva qualquer de \(f\).
Exemplo 3: A função abaixo é uma primitiva de \(z^n\)
$$
\frac{z^{n+1}}{n+1}
$$
para \(n\) inteiro não negativo. A seguinte integral pode ser diretamente avaliada:
$$
\int_{z_{1}}^{z_{2}}z^{n}dz=\frac{1}{n+1}\left. z^{n+1}\right\vert_{z_{1}}^{z_{2}}=\frac{1}{n+1}\left( z_{2}^{n+1}-z_{1}^{n+1}\right).
$$
Uma observação importante será útil na solução de diversos problemas que se apresentarão. Suponha que desejamos calcular a integral de caminho
$$
\oint_{C_{0}}f\left( z\right) \,dz,
$$
onde \(f\left(z\right)\) é analítica em uma região \(R\), exceto em regiões \(R_{1},\; R_{2}\; \text{ e } \; R_{3}\) contidas em \(R\), e \(C_{0}\) é um caminho que envolve as regiões \(R_{1},\; R_{2}\; \text{ e } \; R_{3}\) uma vez no sentido positivo, como representado na figura 5. Podemos construir caminhos arbitrários \(C_{1},\;C_{2}\;\; \text{ e } \;\; C_{3}\) envolvendo estas regiões e, com elas, um novo contorno
$$
C=C_{0}\cup T_{1}\cup -C_{1}\cup -T_{1}\cup T_{2}\cup -C_{2}\cup -T_{2}\cup T_{3}\cup -C_{3}\cup -T_{3},
$$
de forma que \(f\left( z\right)\) é analítica em \(C\) e na região circulada, sendo portanto \(\oint_{C}f\left( z\right) \,dz=0\). Notando que as integrais sobre os caminhos \(T_{i}\) e \(-T_{i} \;\; (i=1,2,3)\) se cancelam restam apenas os termos
$$
0=\oint_{C}f\left( z\right) \,dz=\int_{C_{0}}f\left( z\right)\,dz-\int_{C_{1}}f\left( z\right) \,dz-\int_{C_{2}}f\left( z\right)\,dz-\int_{C_{3}}f\left( z\right) \,dz,
$$
de onde se conclui que
$$
\int_{C_{0}}f\left( z\right) \,dz=\int_{C_{1}}f\left( z\right)
\,dz+\int_{C_{2}}f\left( z\right) \,dz+\int_{C_{3}}f\left( z\right) \,dz.
$$

Cabe notar que o mesmo procedimento pode ser usado para integrar sobre regiões onde existam um número finito arbitrário de regiões onde \(f\left( z\right)\) não é analítica.
Exemplo 4: Se \(C\) é um contorno qualquer envolvendo \(z_0\) uma vez, no sentido positivo, calcule
$$
I=\oint\limits_{C}\frac{dz}{z-z_0}.
$$
Pela observação feita acima verificamos que a integral tem o mesmo resultado se for avaliada ao longo de outro caminho \(C^{\prime }\) qualquer em torno de \(z_0\). Escolheremos então um caminho que admita uma parametrização simples e facilite a solução do problema. Em particular podemos tomar \(C^{\prime }\) como a circunferência de centro em \(z_0\) e raio \(\delta\),
$$
C^{\prime }:\left\vert z-z_0\right\vert =\delta ,
$$

tomando o cuidado de que \(\delta\) seja suficientemente pequeno para que \(C^{\prime }\) esteja inteiramente contida na região interior à \(C\). Neste caso podemos escrever
$$
z-z_0=\delta e^{i\theta },\ 0\leq \theta \leq 2\pi ,
$$
$$
dz=i\delta e^{i\theta }d\theta .
$$
A integral se torna
$$
I=\int_{0}^{2\pi }\frac{i\delta e^{i\theta }d\theta }{\delta e^{i\theta }}
=i\int_{0}^{2\pi }d\theta =2\pi i.
$$
Podemos resumir os resultados acima da seguinte forma:
$$
\oint\limits_{C}\frac{dz}{z-z_0}=\left\{
\begin{array}{ll}
0, & \;\;\text{ se }\;\;C\text{ não envolve }\;z_0 \\
2\pi i,\; & \;\;\text{ se }\;\;C\text{ envolve }\;z_0\text{ uma vez no sentido positivo.}
\end{array}
\right.
$$
Um conceito útil que será estudado com mais detalhes mais tarde é o de singularidades. Se uma função \(f\left( z\right)\) é analítica em toda uma região \(R\subset \mathbb{C}\), exceto em pontos isolados \(z_{i}\) então dizemos que \(z_{i}\) são singularidades isoladas de \(f\). Como exemplos, as funções
$$
f\left( z\right) =\frac{1}{z^{2}+1}\;\; \text{ e } \;\; g\left( z\right) =\frac{z}{\text{sen }z}
$$
possuem singularidades isoladas, respectivamente, em \(z=\pm i\) e \(z=n\pi\;\; \left( n=0,~\pm 1,~\pm 2,\ldots \right)\).
Exercícios:
Verifique se são nulas as seguintes integrais \(\oint\nolimits_{C}f\left( z\right) dz\):
1. \(f\left( z\right) =\frac{z+1}{z-3}\), onde \(C\) é o círculo \(\left\vert z\right\vert =2\).
2. \(f\left( z\right) =\frac{3z^{2}}{z+2i}\), onde \(C\) é o círculo \(\left\vert z\right\vert =\frac{3}{2}\).
3. \(f\left( z\right) =\frac{3ze^{z}}{z^{2}+3}\), onde \(C\) é o círculo \(\left\vert z\right\vert =\frac{5}{4}\).
4. \(f\left( z\right) =\frac{\ln \left( z-2i\right) }{z+2}\), onde \(C\) é o quadrado de vértices \(\pm 1\pm i\).
5. \(f\left( z\right) =\frac{\ln \left( z+1\right) }{z^{2}-9}\), onde \(C\) é o círculo \(x^{2}+y^{2}-2x=0\).
6. \(f\left( z\right) =\frac{\ln \left( z+i\right) }{z^{2}-9}\), onde \(C\) é o círculo \(x^{2}+y^{2}+2x=0\).
7. \(f\left( z\right) =\frac{\ln \left( z-1+i\right) }{z^{2}+9}\), onde \(C\) é o quadrado de vértices \(\pm 1\pm i\).
8. \(f\left( z\right) =\frac{1}{z^{2}}\), onde \(C\) é qualquer caminho que envolve a origem uma vez, no sentido positivo.
9. Calcule a integral de \(f\left( z\right) =1/z\) sobre o caminho \(C\) de \(-i\) até \(i\) passando pelo semiplano \(\text{Re}\left( z\right) >0\).
10. Calcule a integral de \(f\left( z\right) =1/z\) sobre o caminho \(C\) de \(-i\) até \(i\) passando pelo semiplano \(\text{Re}(z) \lt 0\).
11. Combine os resultados dos exercícios (9) e (10) para obter\( \oint\nolimits_{C}\frac{dz}{z}\), onde \(C\) é qualquer caminho que envolve a origem uma vez no sentido positivo.
Outro resultado importante devido a Cauchy é a fórmula da integral. Ela expressa o fato de que uma função analítica em uma região \(R\) fica completamente determinada por seus valores na fronteira de \(R\). Ela também pode ser usada para expressar sob formas integrais todas as derivadas de uma função holomorfa.
Teorema: Seja \(f\) uma função analítica em uma região simplesmente conexa \(R\). Se \(C\) é um contorno fechado inteiramente contido em \(R\) que envolve o ponto \(z_0\) uma vez no sentido positivo então
$$
\oint\limits_{C}\frac{f\left( z\right) }{z-z_0}dz=2\pi if\left(z_0\right).
$$
Demonstração: Iniciamos por reduzir a integração ao contorno
$$
C_{\delta }:\left\vert z-z_0\right\vert =\delta ,
$$
um círculo com centro em \(z_0\) e raio \(\delta\), com \(\delta\) suficientemente pequeno para que \(C_{\delta }\) esteja na região interior à \(C\). Como o integrando é analítico na região hachurada (figura 6) então
$$
\oint\limits_{C\cup -C_{\delta }}\frac{f\left( z\right) }{z-z_0} dz=0\Rightarrow \oint\limits_{C}\frac{f\left( z\right) }{z-z_0} dz=\oint\limits_{C_{\delta }}\frac{f\left( z\right) }{z-z_0}dz.
$$

Defina a função auxiliar
$$
g\left( z\right) =\left\{ \begin{array}{ll}
\frac{f\left( z\right) -f\left( z_0\right) }{z-z_0}, & \;\;\text{ se }\;\; z\neq z_0 \\
f\left( z_0\right) , & \;\;\text{ se }\;\;z=z_0,
\end{array}
\right.
$$
observando que \(g\left( z\right)\) é analítica em \(z_0\). Isto significa que
$$
\oint\limits_{C_{\delta }}g\left( z\right) dz=0=\oint\limits_{C_{\delta }}\frac{f\left( z\right) }{z-z_0}dz-\oint\limits_{C_{\delta }}\frac{f\left(
z_0\right) }{z-z_0}dz.
$$
A segunda integral já foi calculada em um exemplo anterior,
$$
\oint\limits_{C_{\delta }}\frac{f\left( z_0\right) }{z-z_0}dz=f\left(z_0\right) \oint\limits_{C_{\delta }}\frac{dz}{z-z_0}=2\pi if\left(z_0\right) ,
$$
onde \(f\left( z_0\right)\) foi tirado de dentro do sinal de integração por ser uma constante com relação à variável integrada. Fica assim mostrado o teorema.
O teorema acima foi enunciado e demonstrado para valores fixos de \(z_0\). Note, no entanto que nenhuma consideração foi feita para que esse seja um ponto particular no plano complexo. Podemos reafirmar o teorema para pontos variáveis de \(\mathbb{C}\), da seguinte forma: se \(f\) é uma função analítica então ela assume os seguintes valores sobre pontos \(z\) contidos na região interior à \(C\),
$$
f\left( z\right) =\frac{1}{2\pi i}\oint\limits_{C}\frac{f\left( w\right) }{w-z}dw.
$$
A variável de integração foi renomeada para diferenciá-la da variável livre, \(z\). Isto significa que uma função analítica pode ser avaliada no ponto \(z\) interior à curva \(C\) se conhecermos somente seus valores sobre o contorno. Observe que \(z\) é uma singularidade isolada do integrando, embora \(f\left( z\right)\) seja analítica.
Exemplo 5: Usando a fórmula integral de Cauchy podemos calcular
$$
I=\oint\limits_{C}\frac{\text{sen }z}{z-i}dz;\ \text{onde }C:\left\vert z-1\right\vert =2.
$$
O único ponto singular do integrando é \(z=i\), que está na região interior ao contorno \(C\), como mostrado na figura.

Tomamos então \(z_0=i\) e \(f\left( z\right) =\text{sen }z\) para uso da fórmula (1). Como resultado
$$
\oint\limits_{C}\frac{\text{sen }z}{z-i}dz=2\pi if\left( i\right) =\frac{2\pi i}{2i}\left( e^{-1}-e\right) =\pi \left( \frac{1}{e}-e\right).
$$
O cálculo do seno foi feito das seguinte forma: por definição
$$
\text{sen }z=\frac{1}{2i}\left( e^{iz}-e^{-iz}\right) ,
$$
portanto,
$$
\text{sen }i=\frac{1}{2i}\left( e^{-1}-e\right).
$$
Exemplo 6: Para calcular
$$
I=\oint\limits_{C}\frac{zdz}{\left( 9-z^{2}\right) \left( z+i\right) }; \;\; \text{onde }\;\; C:\left\vert z\right\vert =2
$$
observamos que o integrando possui três pontos singulares, que são \(z=-i\) e \(z=\pm 3\). Os pontos \(z=\pm 3\), no entanto, não estão dentro da região envolvida pelo contorno, de modo que podemos tomar
$$
z_0=-i,\ f\left( z\right) =\frac{z}{\left( 9-z^{2}\right) },
$$
e a integral é
$$
I=2\pi if\left( -i\right) =2\pi i\left( \frac{-i}{9+1}\right) =\frac{\pi }{5}.
$$
Exemplo 7: O cálculo da seguinte integral
$$
I=\oint\limits_{C}\frac{dz}{z^{2}+1}
$$
onde \(C\) é o retângulo de vértices \(\pm 2\pm 2i\) pode ser feito de duas formas. Os pontos \(z=\pm i\) são as únicas singularidades do integrando e ambos estão dentro da região limitada pelo contorno \(C\).

A integral pode ser reduzida ao cálculo sobre os contornos \(C_{1}\) e \(C_{2}\), como se mostra na figura, \(
\oint\nolimits_{C}=\oint\nolimits_{C_{1}}+\oint\nolimits_{C_{2}}\), assumindo a seguinte forma:
$$
I=I_{1}+I_{2}=\oint\limits_{C_{1}}\frac{dz}{\left( z+i\right) \left(
z-i\right) }+\oint\limits_{C_{2}}\frac{dz}{\left( z+i\right) \left(
z-i\right) },
$$
onde escrevemos \(z^{2}+1=\left( z+i\right) \left( z-i\right)\). Na primeira destas integrais apenas \(z_0=i\) é um ponto singular. Fazemos \(f\left(z\right) =1/\left( z+i\right)\) e usamos a fórmula da integral
$$
I_{1}=2\pi i~f\left( z_0\right) =2\pi i\frac{1}{2i}=\pi .
$$
Para calcular a segunda integral tomamos \(z_0=-i\) e \(f\left( z\right)=1/\left( z-i\right)\). Usando novamente a fórmula da integral temos
$$
I_{2}=2\pi i~f\left( z_0\right) =2\pi i\frac{-1}{2i}=-\pi ,
$$
de modo que a interal procurada é nula
$$
I=\oint\limits_{C}\frac{dz}{z^{2}+1}=I_{1}+I_{2}=\pi -\pi =0.
$$
Alternativamente, podemos proceder da seguinte forma. Escrevemos o integrando sob forma de frações parciais:
$$
\frac{1}{z^{2}+1}=\frac{1}{\left( z+i\right) \left( z-i\right) }=\frac{A}{z+i}+\frac{B}{z-i}.
$$
Para que a identidade seja satisfeita temos que identificar os numeradores, ou seja
$$
1=A\left( z-i\right) +B\left( z+i\right) =z\left( A+B\right) +i\left(-A+B\right) ,
$$
o que resulta no sistema
$$
\left.
\begin{array}{ll}
~~A+B & =0\ \\
-A+B & =-i,
\end{array}
\right\} \Rightarrow
\begin{array}{ll}
A & =i/2, \\
B & =-i/2.
\end{array}
$$
Verificamos assim que
$$
\frac{1}{z^{2}+1}=\frac{i/2}{z+i}-\frac{i/2}{z-i}
$$
e a integral procurada é
$$
I=\frac{i}{2}\left( \oint\limits_{C}\frac{dz}{z+i}-\oint\limits_{C}\frac{dz}{z-i}\right) =0
$$
pois cada uma das integrais tem a forma de
$$
\oint\limits_{C}\frac{dz}{z-z_0}=2\pi i
$$
onde \(C\) envolve apenas um ponto singular \(z_0\) uma vez, no sentido positivo.
Devemos nos recordar, neste ponto, de que funções reais de uma varíavel real são chamadas de funções analíticas se possuem derivadas de todas as ordens que são, por sua vez, também analíticas. Isto garante que elas possuem uma expansão de Taylor, em séries de potências. Esta terminologia tem origem no estudo das funções de variáveis complexas, devido ao teorema que se segue.
Teorema: Uma função analítica em uma região \(R\) do plano complexo possue derivadas de todas as ordens em \(R\). Estas derivadas são, também, analíticas e podem ser obtidas porderivação direta da fórmula de Cauchy, sendo dadas por
$$
f^{\prime }\left( z\right) =\frac{1}{2\pi i}\oint\limits_{C}\frac{f\left(w\right) }{\left( w-z\right) ^{2}}dw.
$$
Demonstração: Seja \(C\) um contorno fechado simples em \(R\) e \(z\) um ponto na região interior a este contorno. Podemos então escrever
$$
f\left( z\right) =\frac{1}{2\pi i}\oint\limits_{C}\frac{f\left( w\right) }{w-z}dw.
$$
Admitindo a possibilidade de inverter a ordem de operação entre a derivada e a integração obtemos
$$
f^{\prime }\left( z\right) =\frac{df\left( z\right) }{dz}=\frac{1}{2\pi i}
\frac{d}{dz}\oint\limits_{C}\frac{f\left( w\right) }{w-z}dw=\frac{1}{2\pi i}
\oint\limits_{C}\frac{d}{dz}\frac{f\left( w\right) }{w-z}dw.
$$
Observando que \(f\left( w\right)\) é constante, do ponto de vista de variações em \(z\), e
$$
\frac{d}{dz}\frac{1}{w-z}=\frac{1}{\left( w-z\right)^{2}}
$$
chegamos ao resultado que queremos mostrar:
$$
f^{\prime }\left( z\right) =\frac{1}{2\pi i}\oint\limits_{C}\frac{f\left(w\right) }{\left( w-z\right) ^{2}}dw.
$$
Como consequência do teorema podemos obter a derivada segunda derivando mais uma vez a última expressão,
$$
f^{^{\prime \prime }}\left( z\right) =\frac{1}{2\pi i}\oint\limits_{C}\frac{f\left( w\right) }{\left( w-z\right) ^{3}}dw,
$$
ou, por indução, a derivada de qualquer ordem
$$
f^{\left( n\right) }\left( z\right) =\frac{n!}{2\pi i}\oint\limits_{C}\frac{f\left( w\right) }{\left( w-z\right) ^{n+1}}dw.
$$
Exercícios:
1. Demonstre a equação (6).
Use a fórmula da integral de Cauchy para calcular:
2. \( \oint\limits_{\left\vert z-1\right\vert =2}\frac{zdz}{z-2}\)
4. \( \oint\limits_{\left\vert z-2i\right\vert =2}\frac{\text{sen }z}{z-i}dz\)
6. \( \oint\limits_{\left\vert z-1\right\vert =2}\frac{e^{iz}dz}{z+i}\)
8. \( \oint\limits_{\left\vert z-1\right\vert =2}\frac{e^{iz}dz}{\pi -2z}\)
3. \( \oint\limits_{\left\vert z+1\right\vert =2}\frac{zdz}{z+2}\)5. \( \oint\limits_{\left\vert z\right\vert=2}\frac{z\cos z}{z-i}dz\)
7. \( \oint\limits_{\left\vert z\right\vert =1}\frac{izdz}{1-2z}\)
9. \( \oint\limits_{\left\vert z-1\right\vert =2}\frac{e^{z}dz}{z^{2}-4}\)
10. \(\oint\limits_{C}\frac{dz}{z^{2}+1}\) onde \(C\) é o quadrado de vértices \(0\), \(2i,\ \pm 1+i\).
11. \(\oint\limits_{C}\frac{dz}{z^{2}+1}\) onde \(C\) é o quadrado de vértices \(0,-2i,\ \pm 1-i\).
12. \(\oint\limits_{C}\frac{ze^{z}dz}{z^{2}-2z-3}\) onde \(C\) é o losango de vértices \(\pm 2,\ \pm i\).
13. Use a fórmula da derivada para calcular \(\oint\limits_{\left\vert z\right\vert =3}\frac{\cos \left( z^{2}+3z-1\right) }{\left( 2z+3\right)^{2}}dz\)
Algumas respostas:
$$
\begin{array}{lll}
2)\; 4\pi i & 3)\; – 4\pi i & 4)\; \pi \left( 1-e^{2}\right) /e \\
5)\; -\pi \left( e^{2}+1\right) /e \;\; & 6)\; 2\pi ie \;\; & 7)\; \pi /2 \\
8)\; \pi & 9)\; i\pi e^{2}/2 & 10)\; \pi \\
11)\; -\pi & 12)\; \pi i/2e. & 13)\; 0.
\end{array}
$$
Exercício Resolvido:
5) Faça \(f\left( z\right) =z\cos z\), e \(z_0=i\). A integral é, portanto, \(I=2\pi i\left( i\cos i\right)\). Como
$$
\cos z=\frac{1}{2}\left( e^{iz}+e^{-iz}\right) \Rightarrow \cos i=\frac{1}{2} \left( e^{i^{2}}+e^{-i^{2}}\right) =\frac{1}{2}\left( e^{-1}+e\right) ,
$$
temos \(I=-\pi \left( e^{-1}+e\right) =-\pi \left( e^{2}+1\right) /e\).
13) Dada a integral
$$
I=\oint\limits_{\left\vert z\right\vert =3}\frac{\cos \left(z^{2}+3z-1\right) }{\left( 2z+3\right) ^{2}}dz
$$
defina
$$
I\left( w\right) =\oint\limits_{\left\vert z\right\vert =3}\frac{\cos
\left( z^{2}+3z-1\right) }{\left( 2z-2w\right) ^{2}}dz=\frac{1}{4}
\oint\limits_{\left\vert z\right\vert =3}\frac{\cos \left(
z^{2}+3z-1\right) }{\left( z-w\right) ^{2}}dz.
$$
Observe que a integral procurada é \(I=I\left( -3/2\right)\). Pela fórmula da derivada, obtida da fórmula da integral de Cauchy, temos
$$
I\left( w\right) =\frac{1}{4}\frac{d}{dw}\oint\limits_{\left\vert
z\right\vert =3}\frac{\cos \left( z^{2}+3z-1\right) }{z-w}dz,
$$
ond a última integral pode ser avaliada fazendo \(f\left( w\right) =\cos \left( w^{2}+3w-1\right)\). Portanto
$$
I\left( w\right) =\frac{2\pi i}{4}\frac{d}{dw}\left[ f\left( w\right) \right] =\frac{\pi i}{2}\frac{d}{dw}\left[ \cos \left( w^{2}+3w-1\right) \right] .
$$
Esta derivada pode ser obtida diretamente:
$$
I\left( w\right) =-\frac{\pi i}{2}\left[ \text{sen }\left( w^{2}+3w-1\right)\right] \left( 2w+3\right).
$$
A integral procurada é \(I=I\left( -3/2\right) =0\).
Uma função analítica, como vimos, possui derivadas de todas as ordens e suas derivadas são também analíticas3. Por outro lado a integral de uma função analítica, quando integrada sobre um contorno fechado é sempre nula. O teorema seguinte afirma que a recíproca é também verdadeira.
Teorema de Morera: Seja \(f\) uma função contínua em uma região \(R\) satisfazendo \(\oint\nolimits_{C}f\left( z\right) dz=0\) para todo contorno \(C\) em \(R\). Então \(f\) é analítica em \(R\).
Demonstração: Seja\(z_0\) um ponto fixo qualquer de \(R\). A função
$$
F\left( z\right) =\int_{z_0}^{z}f\left( w\right) dw
$$
independe do caminho de integração pois, por hipótese, a integral sobre um caminho fechado é nula. Como no teorema da primitiva, \(F\) é analítica e sua derivada,
$$
\frac{d}{dz}F\left( z\right) =\frac{d}{dz}\int_{z_0}^{z}f\left( w\right)dw=f\left( z\right) ,
$$
é, também, uma funções analítica, o que conclui a demonstração do teorema.
Uma função é chamada de “harmônica” em uma região \(R\) se, nesta região, ela possui derivadas de segunda ordem e satisfaz à equação de Laplace4
$$
\bigtriangledown ^{2}u=\frac{\partial ^{2}u}{\partial x^{2}}+\frac{\partial^{2}v}{\partial x^{2}}=0.
$$
Se \(f\left( z\right) =u\left( x,y\right) +iv\left( x,y\right)\) é analítica em \(R\) então ela possui derivadas de todas as ordens e
$$
\frac{d}{dz}=\frac{\partial }{\partial x}=\frac{\partial }{\partial \left(iy\right) }.
$$
Podemos então derivar as equações de Cauchy-Riemann um número arbitrário de vezes. Derivando uma vez
$$
\left.
\begin{array}{ccc}
u_{x}=v_{y} & \text{(em }x\text{)}\rightarrow & u_{xx}=v_{yx} \\
u_{y}=-v_{x} & \text{(em }y\text{)}\rightarrow & u_{yy}=-v_{xy}
\end{array}
\right\} \Rightarrow u_{xx}+u_{yy}=0,
$$
$$
\left.
\begin{array}{ccc}
u_{x}=v_{y} & \text{(em }y\text{)}\rightarrow & u_{xy}=v_{yy} \\
u_{y}=-v_{x} & \text{(em }x\text{)}\rightarrow & u_{yx}=-v_{xx}
\end{array}
\right\} \Rightarrow v_{xx}+v_{yy}=0,
$$
de onde concluimos que, se \(f\) é analítiva então \(u\left(x,y\right)\) e \(v\left( x,y\right)\) são funções harmônicas.
Uma questão interesssante que segue dai é a seguinte: dada uma função harmônica qualquer ela pode ser considerada parte real ou imaginária de uma função analítica? A resposta é afirmativa, como mostraremos a seguir para o caso geral. Antes disto, porém, vamos mostrar em um exemplo como encontrar a parte imaginária de uma função analítica se conhecemos sua parte real.
Exemplo 8: A função \(u\left( x,y\right)=x^{2}-y^{2}\) é harmônica pois
$$
u_{xx}=2,\ u_{yy}=-2,\ \bigtriangledown ^{2}u=0.
$$
Queremos determinar \(v=\text{Im}\left( f\right)\) de forma que a função \(f=u+iv\) seja analítica. Usando a primeira condição de Cauchy-Riemann
$$
u_{x}=2x=v_{y}
$$
podemos determinar, por integração, que
$$
v=-\int 2xdy=2xy+h\left( x\right)
$$
onde \(h\) é uma função, por enquanto indeterminada, que só pode depender de \(x\). Para encontrar \(h\) usamos a outra condição
$$
u_{y}=-2x=-v_{x}\Rightarrow v_{x}=2x.
$$
Comparando com a equação (7) obtemos
$$
v_{x}=2y+h^{\prime }
$$
de onde concluimos que \(h^{\prime }=0\) e, portanto \(h=c\), uma constante. A função analítica procurada é
$$
f\left( z\right) =x^{2}-y^{2}+2ixy+c=z^{2}+c.
$$
A função \(v\) é a chamada a harmônica conjugada de \(u\).
O caso geral pode ser tratado da seguinte forma: dada \(u\left( x,y\right)\) uma função harmônica procuramos sua harmônica conjugada, \(v\). Sua diferencial será
$$
dv=v_{x}dx+v_{y}dy=-u_{y}dx+u_{x}dy.
$$
Procuramos \(v\) na forma de
$$
v\left( x,y\right) =v_{0}+\int_{\left( x_{0},y_{0}\right) }^{\left(x,y\right) }-u_{y}dx+u_{x}dy,
$$
onde \(v_{0}=v\left( x_{0},y_{0}\right)\). A função \(v\left(x,y\right)\) está bem definida e possui derivadas contúnuas se a integral independe do caminho, ou seja, se \(-u_{y}dx+u_{x}dy\) é uma diferencial exata. Se isto ocorre então \(\oint -u_{y}dx+u_{x}dy=0\) pois \(\oint dv=0\). Para mostrar que este é exatamente o caso denotamos por \(R^{\prime }\) a região interior ao contorno \(C\) e usamos o teorema de Green
$$
\oint -u_{y}dx+u_{x}dy=\iint\nolimits_{R^{\prime }}\left(u_{xx}+u_{yy}\right) =0
$$
sendo que a última integral é nula porque \(u\) é harmônica.
Exercícios :
Mostre que as funções \(u\) dadas abaixo são harmônicas, encontre suas conjugadas harmônicas e as funções analíticas \(f=u+iv\).
$$
\begin{array}{ll}
\text{1.} \; u=x-5xy \;\; & \text{2.} \; u=x-4xy \\
\text{3.}\; u=\text{sen }x \cosh y \;\;\;\; & \text{4.} \; u=x^{3}-3xy^{2}
\end{array}
$$
Algumas respostas:
1. \(f(z)=z+5iz^{2}/2+c,\) 3. \( v=\cos x\text{ senh }y+c, \;\; f(z) =\text{sen }z+ic\).
Uma função \(f:\mathbb{C}\rightarrow \mathbb{C}\) é uma operação que transforma pontos do plano complexo em outros pontos. A cada função de uma variável complexa
$$
w=f\left( z\right) =u\left( x,y\right) +i\left( x,y\right)
$$
estão associadas duas funções reais: \(u\left( x,y\right) =\text{Re}f\left( z\right) \;\text{ e }\; v(x,y)=\text{Im}f\left( z\right)\). Como estas funções levam pontos do plano \(\mathbb{C}\) em pontos de \(\mathbb{C}\) há uma dificuldade natural em se visualizar geometricamente seu efeito. Em algumas situações é útil visualizar funções complexas como transformações. Neste caso se observa como um determinado conjunto de pontos de \(\mathbb{C}\) é levado no próprio \(\mathbb{C}\) pela função.
Exemplo 1: O valor absoluto é uma função que tem como argumento números complexos e retorna números reais: \(\;f:\mathbb{C}\rightarrow \mathbb{R}\). Representaremos esta função por \(\;f(z) = \left\vert z \right\vert\) e a definimos como
$$
w=f\left( z\right) =\left\vert z\right\vert =\sqrt{x^{2}+y^{2}}.
$$
A imagem desta função é \(\mathbb{R}^{+}\).
Exemplo 2: A função
$$
w=f\left( z\right) =\frac{2z-3i}{\left( z-2\right) \left( z+i\right) }
$$
é válida para todos os pontos de \(\mathbb{C}\), exceto \(z=2\) e \(z=-i\). Seu domínio é, portanto, \(D\left(f\right) =\mathbb{C}-\left\{ 2\right\} -\left\{ -i\right\}\).
Exercício Resolvido: Encontre as partes real e imaginária da função
$$
w=\frac{3}{z-5}.
$$
Em coordenadas cartesianas temos
$$
w=\frac{3}{x-5+iy}=\frac{3\left( x-5-iy\right) }{\left( x-5\right) ^{2}+y^{2}}=\frac{3x-15-3iy}{\left( x-5\right) ^{2}+y^{2}}.
$$
Portanto
$$
u\left( x,y\right) = \frac{3x-15}{\left( x-5\right) ^{2}+y^{2}} \;\;\;\;\text{ e }\;\;\;\; v\left( x,y\right) =\frac{3y}{\left( x-5\right) ^{2}+y^{2}}
$$
são as partes real e imaginária, respectivamente.
Algumas definições são necessárias para prosseguirmos nosso estudo.
Definição: Se \(z_{0}\) é um ponto de acumulação do domínio \(D\) de uma função \(f\) então
$$
\lim_{z\rightarrow z_{0}}f\left( z\right) =L
$$
se, dado qualquer \(\epsilon >0\) existe um \(\delta >0\) tal que
$$
z\in D,\;0<\left\vert z-z_{0}\right\vert <\delta \Rightarrow \left\vert f\left( z\right) -L\right\vert <\epsilon .
$$
Equivalentemente:
$$
z\in D\cap V_{\delta }\left( z_{0}\right) \Rightarrow f\left( z\right) \in V_{\varepsilon }\left( L\right).
$$
Definição: Se \(\lim_{z\rightarrow z_{0}}f\left( z\right) =f\left( z_{0}\right)\) então \(f\) é contínua em \(z_{0}\).
Teorema: Seja \(f=u+iv\) e \(L=U+iV\). Então
$$
\lim_{z\rightarrow z_{0}}f\left( z\right) =L\Longleftrightarrow \lim_{z\rightarrow z_{0}}u=U\text{ }\;\;\;\;\;\text{ e }\;\;\;\;\lim_{z\rightarrow z_{0}}v=V.
$$
Corolário: Uma função \(f\left(z\right) =u\left( x,y\right) +iv\left( x,y\right)\) é contínua se, e somente se, as funções \(u\) e \(v\) são contínuas.
Teorema: Se \(\lim_{z\rightarrow z_{0}}f\left( z\right) =F\) e \(\lim_{z\rightarrow z_{0}}g\left( z\right) =G\) então
(c) \(\lim_{z\rightarrow z_{0}}\left[ f\left( z\right) /g(z)\right] =F/G\), se \(G\neq 0\).
Teorema: Se \(\lim_{z\rightarrow z_{0}}f\left( z\right) =F\) então existe uma vizinhança \(V_{\delta }\left( z_{0}\right)\) onde \(f\left(z\right)\) é limitada.
Teorema: A soma e o produto de funções contínuas são contínuas. O quociente é contínuo se o denominador não se anula.
Diferente do que acontece com as funções de uma variável real, quando se analisa o comportamento de uma função de uma variável complexa na vizinhança de um ponto \(z_{0}\) é necessário considerar os diferentes caminhos tomados para se chegar a \(z_{0}\) no plano complexo. De modo análogo ao que ocorre com funções de duas variáveis reais, diremos que uma função \(f:D\rightarrow \mathbb{C}\) é derivável em \(z_{0}\) se sua derivada não depende do caminho tomado para se chegar a \(z_{0}\).
Definição: Uma função \(f:D\rightarrow \mathbb{C}\) é derivável em \(z\in D\) se existe o limite
$$
\lim_{\Delta z\rightarrow 0}\frac{f\left( z+\Delta z\right) -f\left(
z\right) }{\Delta z}\equiv f^{\prime }\left( z\right).
$$
Este limite deve ser único, não podendo depender de como \(z+\Delta z\) se aproxima de \(z\) ou, equivalentemente, de como \(\Delta z\rightarrow 0\).
Exemplo 3: A função \(f\left( z\right) =\left\vert z\right\vert ^{2}\) não é derivável em nenhum ponto de \(\mathbb{C}\). Para ver isto fazemos \(f\left( z\right) =\left\vert z\right\vert ^{2}=z \bar{z}\) e, usando a definição,
$$
f^{\prime }\left( z\right) =\lim_{\Delta z\rightarrow 0}\frac{\left(
z+\Delta z\right) \left( \bar{z}+\Delta \bar{z}\right) -z\bar{z}}{\Delta z}
=\lim_{\Delta z\rightarrow 0}\frac{z\Delta \bar{z}}{\Delta z}+\Delta \bar{z}+
\bar{z}.
$$
Escrevendo o incremento em forma polar,
$$
\Delta z=re^{i\theta };\ \Delta \bar{z}=re^{-i\theta },
$$
e lembrando que \(\Delta z\rightarrow 0\) equivale a \(r\rightarrow 0\) temos que
$$
f^{\prime }\left( z\right) =\lim_{r\rightarrow 0}\ \left( ze^{-2i\theta
}+re^{-i\theta }+\bar{z}\right) =ze^{-2i\theta }+\bar{z}.
$$
Observe que este limite depende do ângulo \(\theta\) com que se aproxima de \(z\) e, portanto, o limite não é único. Dizemos que esta função só tem derivada no ponto \(z=0\) e, neste ponto, \(f^{\prime}\left( 0\right) =0\).
Definição: Uma função \(f:D\rightarrow \mathbb{C}\) é analítica em uma região \(R\) se é derivável em cada ponto de \(R\). \(f\) é analítica no ponto \(z_{0}\) se é analítica numa vizinhança \(V_{\delta }\left( z_{0}\right)\). Uma função é dita inteira se for analítica em todo o plano complexo. As expressões holomorfa ou regular são também empregadas.
As funções elementares, extendidas para o plano complexo, são analíticas. Veremos alguns exemplos simples deste fato.
Exemplo 4: A função contínua \(f\left( z\right)=z_0\;\) (uma constante) é analítica e sua derivada é nula em todo ponto.
Exemplo 5: Se \(f\left( z\right) =z^{2}\) então
$$
f^{\prime }\left( z\right) =\lim_{\Delta z\rightarrow 0}\frac{f\left(
z+\Delta z\right) -f\left( z\right) }{\Delta z}=\lim_{\Delta z\rightarrow 0}
\frac{\left( z+\Delta z\right) ^{2}-z^{2}}{\Delta z}=
$$
$$
= \lim_{\Delta z\rightarrow 0}\frac{2z\Delta z+\Delta z^{2}}{\Delta z}==\lim_{\Delta z\rightarrow 0}2z+\Delta z=2z.
$$
Observe que este limite não depende de como \(\Delta z\rightarrow 0\). Usando o binômio de Newton podemos generalizar este resultado para funções \(f\left( z\right) =z^{n}\), cujas derivadas são
$$
f^{\prime }\left( z\right) =nz^{n-1}.
$$
Observamos que a soma e o produto de funções analíticas são analíticas. O quociente é analítico se o denominador for não-nulo. As seguintes regras se aplicam:
| a. \(\left(f+g\right)^{\prime}=f^{\prime}+g^{\prime }\) |
| b. \(\left(fg\right)^{\prime}=f^{\prime}g+fg^{\prime }\) |
| c. \(\left(\frac{f}{g}\right)^{\prime}=\frac{f^{\prime}g-fg^{\prime }}{g^{2}},\;\;\text{ se }\;\;g\neq 0\). |
Além disto temos um resultado importante: se \(f\) é uma função derivável em \(z_{0}\) então ela é contínua neste ponto. Para ver isto notamos que
$$
f^{\prime }\left( z_{0}\right) =\lim_{z\rightarrow z_{0}}\frac{f\left(z\right) -f\left( z_{0}\right) }{z-z_{0}}.
$$
Definimos
$$
g\left( z\right) =\frac{f\left( z\right) -f\left( z_{0}\right) }{z-z_{0}}-f^{\prime }\left( z_{0}\right)
$$
e, portanto,
$$
\lim_{z\rightarrow z_{0}}g\left( z\right) =0.
$$
De (1) podemos escrever
$$
f\left( z\right) =f\left( z_{0}\right) +\left( z-z_{0}\right) g\left(z\right) +\left( z-z_{0}\right) f^{\prime }\left( z_{0}\right)
$$
e, desta última expressão
$$
\lim_{z\rightarrow z_{0}}f\left( z\right) =f\left( z_{0}\right).
$$
Logo ela é contínua.
Exemplo 6: A função
$$
f\left( z\right) =\frac{\left( z+i\right) \left( 3z+1\right) ^{2}}{z\left(z-i\right) \left( z+2\right) ^{2}}
$$
só deixa de ser analítica nos pontos \(z=0\), \(z=i\) e \(z=-2\).
Seja \(f\left( z\right) =u+iv\) uma função derivável em \(z=x+iy\). Então o limite
$$
\lim_{\Delta z\rightarrow 0}\frac{f\left( z-\Delta z\right) -f\left(
z\right) }{\Delta z}=f^{\prime }\left( z\right)
$$
existe e independe de como \(\Delta z\rightarrow 0\). Tomamos em particular dois caminhos. Fazendo \(\Delta z=k\), que corresponde a \(z\) se aproximando de \(z_{0}\) ao longo do eixo real, temos
$$
f^{\prime }\left( z\right) =\lim_{k\rightarrow 0}\frac{1}{k}\left[ u\left(
x+k,y\right) +iv\left( x+k,y\right) -u\left( x,y\right) -iv\left( x,y\right)
\right]
$$
$$
=\lim_{k\rightarrow 0}\frac{1}{k}\left[ u\left( x+k,y\right) -u\left(
x,y\right) +iv\left( x+k,y\right) -iv\left( x,y\right) \right] =
$$
$$
=\frac{\partial u\left( x,y\right) }{\partial x}+i\frac{\partial v\left(
x,y\right) }{\partial x}.
$$
Por outro lado, fazendo \(\Delta z=it\), o que corresponde a tomar \(z\) se aproximando de \(z_{0}\) ao longo do eixo imaginário, temos
$$
f^{\prime }\left( z\right) =\lim_{t\rightarrow 0}\frac{1}{it}\left[ u\left(x,y+t\right) +iv\left( x,y+t\right) -u\left( x,y\right) -iv\left( x,y\right)
\right].
$$
Para explicitar as partes real e imaginária deste limite multiplicamos numerador e denominador por \(-i\),
$$
f^{\prime }\left( z\right) =\lim_{t\rightarrow 0}\frac{1}{t}\left[ v\left(x,y+t\right) -v\left( x,y\right) -iu\left( x,y+t\right) +iu\left( x,y\right) \right] =
$$
$$
=\frac{\partial v\left( x,y\right) }{\partial y}-i\frac{\partial u\left(x,y\right) }{\partial y}.
$$
Para que a função seja derivável os limites tomados para os dois casos devem ser iguais. Identificando as partes reais e imaginárias chegamos às equações de Cauchy-Riemann:
$$
\frac{\partial u\left( x,y\right) }{\partial x}=\frac{\partial v\left(x,y\right) }{\partial y};
$$
$$
\frac{\partial u\left( x,y\right) }{\partial y}=-\frac{\partial v\left(x,y\right) }{\partial x}.
$$
Para simplificar a notação faremos
$$
\frac{\partial u}{\partial x}=u_{x};\;\ \frac{\partial v}{\partial y}=v_{y};\ \;\frac{\partial u}{\partial y}=u_{y};\ \;\frac{\partial v}{\partial x}=v_{x},
$$
de forma que as equações de Cauchy-Riemann podem ser escritas simplesmente como
$$
u_{x}=v_{y};\;\;\ \;u_{y}=-v_{x}.
$$
Estas condições, no entanto, são necessárias mas não suficientes para que \(f=u+iv\) seja uma função analítica. O seguinte teorema exibe as condições para que isto seja verdadeiro.
Teorema: Sejam \(u\left( x,y\right)\) e \(v\left(x,y\right)\) funções reais com derivadas parciais contínuas numa região \(R\). Então as equações de Cauchy-Riemann são condições necessárias e suficientes para que \(f=u+iv\) seja analítica.
Observe que, para uma função analítica, podemos tomar\ \(\Delta z\rightarrow 0\) ao longo de qualquer caminho, em particular podemos fazer \(\Delta z=\Delta x\), como fizemos na derivação das equações de Cauchy-Riemann. Sua derivada é, portanto
$$
\frac{df\left( z\right) }{dz}=\frac{\partial f\left( z\right) }{\partial x}.
\label{dparc}
$$
Se for conveniente podemos também usar a derivada parcial em \(y\).
Exemplo 8: A função \(f\left( z\right) =\bar{z}\) não é analítica. Note que \(\bar{z}=x-iy\). Dai
$$
u\left( x,y\right) =x,\; v\left( x,y\right) =-y,\; u_{x}=1,\; v_{x}=0,\; u_{y}=0,v_{y}=-1.
$$
Exemplo 9: Como já sabemos a função \(f\left(z\right) =z^{2}\) é analítica. Observe que, em coordenadas cartesianas,
$$
f\left( z\right) =\left( x+iy\right) ^{2}=x^{2}-y^{2}+2xyi.
$$
Suas partes real e imaginária são
$$
u\left( x,y\right) =x^{2}-y^{2};\ \ v\left( x,y\right) =2xy
$$
e suas derivadas parciais
$$
\begin{array}{ll}
\frac{\partial u}{\partial x}=2x, & \frac{\partial v}{\partial y}=2x \\
\frac{\partial u}{\partial y}=-2y,\ \ \ \ & \frac{\partial v}{
\partial x}=2y.
\end{array}
$$
Como \(u_{x}=v_{y}\), \(\ u_{y}=-v_{x}\) e as derivadas parciais são contínuas então a função é analítica. Sua derivada é, usando (2),
$$
\frac{dz^{2}}{dz}=\frac{\partial z^{2}}{\partial x}=u_{x}+iv_{x}=2x+2iy=2z.
$$
Exemplo 10: Vamos verificar que se a função \(f\left(z\right) =1/z\) é analítica e encontrar sua derivada. Precisamos primeiro escrever a função de forma a explicitar sua parte real e imaginária,
$$
f\left( z\right) =\frac{1}{z}=\frac{1}{x+iy}=\frac{1}{x+iy}\frac{x-iy}{x-iy}=
\frac{x-iy}{x^{2}+y^{2}}.
$$
Portanto
$$
u\left( x,y\right) =\frac{x}{x^{2}+y^{2}},\;\;\;v\left( x,y\right) =\frac{-y}{x^{2}+y^{2}}.
$$
Lembrando que a derivada de um quociente é
$$
\left( \frac{f}{g}\right) ^{\prime }=\frac{f^{\prime }g-fg^{\prime }}{g^{2}}
$$
calculamos
$$
u_{x}=\frac{x^{2}+y^{2}-x\left( 2x\right) }{\left( x^{2}+y^{2}\right) ^{2}}=
\frac{y^{2}-x^{2}}{\left( x^{2}+y^{2}\right) ^{2}},
$$
$$
u_{y}=\partial _{y}\left[ x\left( x^{2}+y^{2}\right) ^{-1}\right] =\frac{-2xy}{\left( x^{2}+y^{2}\right) ^{2}},
$$
$$
v_{x}=\partial _{x}\left[ -y\left( x^{2}+y^{2}\right) ^{-1}\right] =\frac{2xy}{\left( x^{2}+y^{2}\right) ^{2}},
$$
$$
v_{y}=-\frac{x^{2}-y^{2}}{\left( x^{2}+y^{2}\right) ^{2}}=\frac{y^{2}-x^{2}}{\left( x^{2}+y^{2}\right) ^{2}}.
$$
Observamos que as equações de Cauchy-Riemann, \(u_{x}=v_{y},\;u_{y}=-v_{x},\;\) são satisfeitas em todo o plano complexo. No entanto as derivadas parciais de \(u\) e \(v\) não são contínuas em \(\left(x,y\right) =\left( 0,0\right)\) de onde concluímos que \(f\left(z\right)\) é analítica em \(\mathbb{C}-\left\{ 0\right\}\). Fora de \(z=0\) a função é analítica e podemos usar (2) para obter sua derivada:
$$
\frac{d}{dz}\left( \frac{1}{z}\right) =\frac{\partial }{\partial x}\left(\frac{1}{z}\right) =\frac{\partial }
{\partial x}\left( \frac{x-iy}{x^{2}+y^{2}}\right) =-\frac{1}{z^{2}}.
$$
Obtenha, como um exercício, a última igualdade.
Exercício Resolvido: Verifique se são analíticas e em que região são analíticas as funções:
a. \(f(z)=e^z\) b. \(f(z) =z\bar{z}\) c. \(f(z) =1\)
Encontre as derivadas das funções, quando existirem.
a. A função exponencial pode ser escrita como
$$
f\left( z\right) =e^{z}=e^{x+iy}=e^{x}e^{iy}=e^{x}\left( \cos y+i\text{sen }y\right).
$$
Portanto
$$
u\left( x,y\right) =e^{x}\cos y\;\;\;\Rightarrow \;\;\;u_{x}=e^{x}\cos y,\;\;\;u_{y}=-e^{x}\text{sen }y
$$
$$
v\left( x,y\right) =e^{x}\text{sen }y\;\;\;\Rightarrow \;\;v_{x}=e^{x}\text{sen }y,\;\;\;v_{y}=e^{x}\cos y.
$$
Como as condições de Cauchy Riemann são satisfeitas e as derivadas parciais são contínuas a função é analítica em todo o plano complexo. Além disto sua derivada é
$$
\frac{d\,e^{z}}{dz}=\frac{\partial \,e^{z}}{\partial x}=u_{x}+iv_{x}=e^{x}\cos y+ie^{x}\text{sen }y=e^{x}e^{iy}=e^{z}.
$$
b. A função \(f\left( z\right) =z\bar{z}=(x+iy)\left( x-iy\right)=x^{2}+y^{2}\) só é analítica em \(z=0\) pois
$$
u\left( x,y\right) =x^{2}+y^{2}\;\;\;\Rightarrow \;\;\;u_{x}=2x,\;\;\;u_{y}=2y
$$
$$
v\left( x,y\right) =0\;\;\;\Rightarrow \;\;v_{x}=0,\;\;\;v_{y}=0.
$$
c. Já a função constante \(f\left( z\right) =1\) é analítica em \(\mathbb{C}\) pois \(u=1,\;v=0\), e todas as derivadas são nulas, portanto contínuas. Sua derivada é
$$
\frac{d\,1}{dz}=\frac{\partial \,1}{\partial x}=0.
$$
Algumas vezes é mais fácil trabalhar com as funções em coordenadas polares para testar sua analiticidade. Para obter as equações de Cauchy-Riemann nestas coordenadas partimos das relações entre as coordenadas polares e as coordenadas cartesianas,
$$
r\left( x,y\right) =\sqrt{x^{2}+y^{2}};\;\;\theta \left( x,y\right) =\arctan\left( \frac{y}{x}\right)
$$
ou, inversamente,
$$
x=r\cos \theta ,\ \ y=r\text{sen }\theta .
$$
Se \(f\) é uma função de \(x\) e \(y\), que, por sua vez, são funções de \(r\) e \(\theta\),
$$
f=f\left( x\left( r,\; \theta \right) ,\;\; y\left( r,\; \theta \right) \right)
$$
podemos relacionar as derivadas parciais calculadas nos dois sistemas de coordenadas por meio da regra da cadeia:
$$
\frac{\partial f}{\partial r}=\frac{\partial f}{\partial x}\frac{\partial x}{
\partial r}+\frac{\partial f}{\partial y}\frac{\partial y}{\partial r},
$$
$$
\frac{\partial f}{\partial \theta }=\frac{\partial f}{\partial x}\frac{
\partial x}{\partial \theta }+\frac{\partial f}{\partial y}\frac{\partial y}{
\partial \theta }.
$$
Como estas duas relações são válidas independentemente da função \(f\) considerada podemos escrever as relações de operadores,
$$
\frac{\partial }{\partial r}=\frac{\partial }{\partial x}\frac{\partial x}{
\partial r}+\frac{\partial }{\partial y}\frac{\partial y}{\partial r},
$$
$$
\frac{\partial }{\partial \theta }=\frac{\partial }{\partial x}\frac{
\partial x}{\partial \theta }+\frac{\partial }{\partial y}\frac{\partial y}{
\partial \theta }.
$$
Precisaremos das derivadas
$$
\begin{array}{ll}
x_{r}=\cos \theta , & y_{r}=\text{sen }\theta , \\
x_{\theta }=-r\text{sen }\theta ,\ \ \ & y_{\theta }=r\cos \theta .
\end{array}
$$
Então
$$
\frac{\partial }{\partial r}=\cos \theta \frac{\partial }{\partial x}+\text{
sen}\theta \frac{\partial }{\partial y},\; \; \; \; \frac{\partial }{
\partial \theta }=-r\text{sen }\theta \frac{\partial }{\partial x}+r\cos
\theta \frac{\partial }{\partial y}.
$$
Em particular
$$
\begin{array}{ll}
u_{r}=\cos \theta ~u_{x}+\text{sen }\theta ~u_{y}, & v_{r}=\cos \theta ~v_{x}+
\text{sen }\theta ~v_{y}, \\
u_{\theta }=-r\text{sen }\theta ~u_{x}+r\cos \theta ~u_{y},\; \; \; \; &
v_{\theta }=-r\text{sen }\theta ~v_{x}+r\cos \theta ~v_{y}.
\end{array}
$$
Usando as equações de Cauchy-Riemann em coordenadas cartesianas (\(u_{x}=v_{y}\) e \(u_{y}=-v_{x}\) ) podemos escrever
$$
\begin{array}{ll}
u_{r}=\cos \theta & v_{y}-\text{sen }\theta ~v_{x}=\frac{1}{r}v_{\theta }, \\
u_{\theta }=-r\text{sen }\theta & v_{y}-r\cos \theta ~v_{x}=-rv_{r}.
\end{array}
$$
Estas são, portanto, as equações de Cauchy-Riemann em coordenadas polares:
$$
\frac{\partial u}{\partial r}=\frac{1}{r}\frac{\partial v}{\partial \theta },
$$
$$
\frac{\partial v}{\partial r}=-\frac{1}{r}\frac{\partial u}{\partial \theta}.
$$
Observe que, se a função é analítica, sua derivada é
$$
\frac{df\left( z\right) }{dz}=\frac{\partial f\left( z\right) }{\partial x}.
$$
A derivada parcial em \(x\) pode ser associada às derivadas em \(r\) e \(\theta\) da seguinte forma: primeiro calculamos as derivadas parciais
$$
\frac{\partial r}{\partial x}=\frac{\partial }{\partial x}\sqrt{x^{2}+y^{2}}=\frac{x}{\sqrt{x^{2}+y^{2}}}=\frac{x}{r}=\cos \theta,
$$
$$
\frac{\partial \theta }{\partial x}=\frac{\partial }{\partial x}\text{arctag } \left( \frac{y}{x}\right) =\frac{1}{1+\left( y/x\right) ^{2}}\frac{-y}{x^{2}}
=\frac{-y}{x^{2}+y^{2}}=\frac{-\text{sen }\theta }{r}.
$$
Em seguida, usando a regra da cadeia, temos
$$
\frac{\partial }{\partial x}=\frac{\partial }{\partial r}\frac{\partial r}{
\partial x}+\frac{\partial }{\partial \theta }\frac{\partial \theta }{
\partial x}=\cos \theta \frac{\partial }{\partial r}-\frac{\text{sen }\theta
}{r}\frac{\partial }{\partial \theta }
$$
portanto
$$
\frac{df\left( z\right) }{dz}=\cos \theta \frac{\partial f\left( z\right) }{
\partial r}-\frac{\text{sen }\theta }{r}\frac{\partial f\left( z\right) }{
\partial \theta }.
$$
Apenas como referência vamos listar a derivada parcial em \(y:\)
$$
\frac{\partial }{\partial y}=\frac{\partial }{\partial r}\frac{\partial r}{
\partial y}+\frac{\partial }{\partial \theta }\frac{\partial \theta }{
\partial y}=\text{sen }\theta \frac{\partial }{\partial r}+\frac{\cos \theta
}{r}\frac{\partial }{\partial \theta },
$$
enquanto \(r\) e \(\theta\) tem derivadas em \(y\)
$$
\frac{\partial r}{\partial y}=\frac{\partial }{\partial y}\sqrt{x^{2}+y^{2}}=
\frac{y}{\sqrt{x^{2}+y^{2}}}=\frac{r\text{sen }\theta }{r^{2}}=\text{sen }
\theta ,
$$
$$
\frac{\partial \theta }{\partial y}=\frac{\partial }{\partial y}\text{arctag}
\left( \frac{y}{x}\right) =\frac{1}{1+\left( y/x\right) ^{2}}\frac{1}{x}=
\frac{x}{x^{2}+y^{2}}=\frac{\cos \theta }{r}.
$$
Exemplo 11: Vamos verificar se a função \(f\left(z\right) =1/z\) é analítica. Já resolvemos este exercício em coordenadas cartesianas mas vale notar que a verificação fica mais simples em coordenadas polares. Para isto escrevemos
$$
f\left( z\right) =\frac{1}{z}=\frac{1}{re^{i\theta }}=\frac{e^{-i\theta }}{r}
=\frac{1}{r}\left( \cos \theta -i\text{sen }\theta \right).
$$
Portanto
$$
u\left( r,\theta \right) =\frac{1}{r}\cos \theta ,\;\;\;v\left( r,\theta
\right) =-\frac{1}{r}\text{sen }\theta .
$$
Calculamos agora
$$
u_{r}=-\frac{1}{r^{2}}\cos \theta ,\;\;\;\;\;u_{\theta }=-\frac{1}{r}
\text{sen }\theta ,
$$
$$
v_{r}=\frac{1}{r^{2}}\text{sen }\theta, \;\;\;\;\;\;v_{\theta }=-\frac{1}{r}\cos \theta.
$$
portanto \(u_{r}=\frac{1}{r}v_{\theta },\;v_{r}=-\frac{1}{r}u_{\theta }\), as equações de Cauchy-Riemann são satisfeitas. No entanto as derivadas parciais não são contínuas em \(r=0\) logo \(f\left(z\right)\) não é analítica em \(z=0,\;\) como já havíamos concluído usando a representação em coordenadas cartesianas.
Exemplo 12: Verifique se a função \(f\left( z\right) =1/z^{2}\) é analítica. Escrevemos a função em coordenadas polares,
$$
f\left( z\right) =\frac{1}{z^{2}}=\frac{1}{r^{2}e^{2i\theta }}=\frac{
e^{-2i\theta }}{r^{2}}=\frac{1}{r^{2}}\left( \cos 2\theta -i\text{sen }
2\theta \right).
$$
Portanto
$$
u\left( r,\theta \right) =\frac{1}{r^{2}}\cos 2\theta ,\;\;\;v\left(
r,\theta \right) =-\frac{1}{r^{2}}\text{sen }2\theta .
$$
As derivadas parciais de \(u\) e \(v\), em coordenadas polares, são
$$
u_{r}=-\frac{2}{r^{3}}\cos 2\theta ,\;\;\;\;\;u_{\theta }=-\frac{2}{r^{2}}\text{sen }2\theta ,
$$
$$
v_{r}=\frac{2}{r^{3}}\text{sen }2\theta ;\;\;\;\;\;\;v_{\theta }=-\frac{2}{
r^{2}}\cos 2\theta .
$$
portanto \(u_{r}=\frac{1}{r}v_{\theta },\;v_{r}=-\frac{1}{r}u_{\theta }\). As derivadas parciais não são contínuas em \(r=0\;\;\) logo \(f\left(z\right)\) não é analítica em \(r=0\).
Exercício Resolvido: Verifique se são analíticas e em que região são analíticas:
a. \(f\left( z\right) =\frac{1}{z^{3}},\;\;\;\)b.\( \; f\left( z\right) =\sqrt{z}\).
Para estas funções é mais fácil fazer o teste em coordenadas polares.
a. Escrevemos \(z=re^{i\theta }\), logo
$$
f\left( z\right) =\frac{1}{z^{3}}=\frac{1}{r^{3}e^{3\theta i}} =r^{-3}\left( \cos 3\theta -i\text{sen }3\theta \right).
$$
Foi usado aqui
$$
\frac{1}{e^{3\theta i}}=e^{-3\theta i}=\cos \left( -3\theta \right) +i \text{sen }\left( -3\theta \right) =\cos 3\theta -i\text{sen }3\theta ,
$$
pois o cosseno é uma função par enquanto o seno é impar. Temos então
$$
u=r^{-3}\cos 3\theta \;\;\;\Rightarrow \;\;\;u_{r}=-3r^{-4}\cos 3\theta ,\;\;\;u_{\theta }=-3r^{-3}\text{sen }3\theta
$$
$$
v=-r^{-3}\text{sen }3\theta \;\;\;\Rightarrow \;\;v_{r}=3r^{-4}\text{sen }3\theta ,\;\;\;v_{\theta }=-3r^{-3}\cos 3\theta .
$$
Então a função é analítica, exceto em \(z=0\), onde as derivadas parciais não são contínuas. Observe que neste ponto a função nem mesmo está definida.
b. Escrevemos \(z=re^{i\theta }\) e tomamos uma de suas raízes, observando que o mesmo resultado seria obtido com a outra raiz,
$$
f\left( z\right) =\sqrt{z}=\sqrt{re^{i\theta }}=\sqrt{r}e^{i\theta /2}=\sqrt{r}\left( \cos \frac{\theta }{2}+i\text{sen }\frac{\theta }{2}\right).
$$
Temos então
$$
u=\sqrt{r}\cos \frac{\theta }{2}\;\;\;\Rightarrow \;\;\;u_{r}=\frac{1}{2\sqrt{r}}\cos \frac{\theta }{2},\;\;\;u_{\theta }=-\frac{\sqrt{r}}{2}\text{
sen}\frac{\theta }{2},
$$
$$
v=\sqrt{r}\text{sen }\frac{\theta }{2}\;\;\;\Rightarrow \;\;v_{r}=\frac{1}{2
\sqrt{r}}\text{sen }\frac{\theta }{2},\;\;\;v_{\theta }=\frac{\sqrt{r}}{2}
\cos \frac{\theta }{2}.
$$
Então a função é analítica exceto em \(z=0\). Note que a função está definida em \(z=0\) mas suas derivadas parciais, \(u_{r}\) e \(v_{r}\), não são contínuas neste ponto.
Exercício Resolvido: Verifique se é analítica a função logaritmo, \(f\left( z\right) =\ln z=\ln \left(re^{i\theta }\right)\).
Observe que o logaritmo, que voltaremos a estudar ainda neste capítulo, pode ser escrito da seguinte forma, usando a propriedade \(\ln \left(ab\right) =\ln a+\ln b:\)
$$
\ln z=\ln \left( re^{i\theta }\right) =\ln r+\ln e^{i\theta }=\ln r+i\theta ,
$$
para \(0\leq \theta \leq 2\pi\). Nesta região temos
$$
u\left( r,\theta \right) =\ln r,\ \ v\left( r,\theta \right) =\theta .
$$
As derivadas parciais são
$$
\begin{array}{lll}
u_{r}=\frac{1}{r}, & & v_{\theta }=0, \\
v_{r}=0, & & v_{\theta }=1,
\end{array}
$$
e, portanto a função é analítica em todo o plano complexo exceto na origem, onde \(u_{r}\) não é contínua.
Para o estudo que se segue será útil fazer uma revisão dos conceitos de curva de nível e gradiente. Dada uma função de duas variáveis, \(z=u\left( x,y\right)\), então \(u\left( x,y\right) =k\), uma constante, formam famílias de curvas em \(\mathbb{R}^{2}\), cada curva correspondendo a um valor da constante \(k\). Estas são as chamadas curvas de nível de \(u\) consistindo no conjunto de pontos de \(\mathbb{R}^{2}\) que são levados no mesmo valor \(k\) pela função \(u\). Definimos o gradiente de \(u\) como o vetor
$$
\text{grad}u=\vec{\bigtriangledown}u=\left( \frac{\partial u}{\partial x},~
\frac{\partial u}{\partial y}\right)
$$
e observamos que o gradiente é perpendicular a um vetor tangente às curvas de nível, como ilustrado na figura. Para ver isto note que, sobre as curvas de nível, temos \(u\left( x,y\right) =k\) e portanto
$$
0=du=\frac{\partial u}{\partial x}dx+\frac{\partial u}{\partial y}dy=\left(
\frac{\partial u}{\partial x},~\frac{\partial u}{\partial y}\right) \cdot
\left( dx,~dy\right).
$$
Em outros termos temos
$$
\vec{\bigtriangledown}u\cdot d\vec{x}=0\Rightarrow \vec{\bigtriangledown} u\bot d\vec{x}.
$$

Podemos agora enunciar o seguinte teorema:
Teorema: Se a função \(f=u+iv\) é analítica em uma região \(R\) então as curvas de nível das famílias \(u\left( x,y\right) = \; \text{ constante e } \; v\left( x,y\right) =\) constante se cruzam em ângulo reto (são ortogonais) em todo ponto \(z_{0}\in R\) satisfazendo \(\;f^{\prime }\left( z_{0}\right) \neq 0\).
Demonstração: \(\text{grad}u=\vec{\bigtriangledown} u=\left( u_{x},~u_{y}\right)\) é normal às curvas \(u=\) cte enquanto \(\vec{\bigtriangledown}v=\left( v_{x},~v_{y}\right)\) é normal às curvas \(v=\) cte. Tomamos o produto escalar
$$
\vec{\bigtriangledown}u\cdot \vec{\bigtriangledown}v=\left(
u_{x},~u_{y}\right) \cdot \left( v_{x},~v_{y}\right) =u_{x}v_{x}+u_{y}v_{y}.
$$
Usando as condições de Cauchy-Riemann para a analiticade de \(f\) temos
$$
\vec{\bigtriangledown}u\cdot \vec{\bigtriangledown}v=-u_{x}u_{y}+u_{y}u_{x}=0,
$$
de onde concluímos que \(\vec{\bigtriangledown}u\bot \vec{\bigtriangledown}v\).
Observe que estas curvas, \(u\) e \(v\) constante, são curvas no domínio da função no plano complexo, representado pelas coordenadas \(z=x+iy\) como ilustrado na figura. As curvas \(u\) e \(v\) constante na imagem, \(w=f\left( z\right)\) são perpendiculares por definição.
Exemplo 13: Vamos verificar a perpendicularidade estudada acima para a função
$$
w=z^{2}=x^{2}-y^{2}+2ixy.
$$
As curvas \(u\left( x,y\right) =k\) são as hipérboles
$$
x^{2}-y^{2}=k_{1}\Rightarrow \frac{x^{2}}{k_{1}}-\frac{y^{2}}{k_{1}}=1,
$$
enquanto \(v\left( x,y\right) =k\) são também hipérboles, dadas por
$$
2xy=k_{2}\Rightarrow y=\frac{k_{2}}{2x}.
$$
Algumas vezes é útil considerar o último teorema sob a seguinte
forma:
Teorema: Se a função \(f=u+iv\) é analítica em uma região \(R\) então as famílias de curvas
parametrizadas por \(x\) e \(y\) respectivamente, são ortogonais em \(z_{0}\in R\), desde que \(f^{\prime }\left( z_{0}\right) \neq 0\).
Demonstração: Em forma vetorial as famílias \(F_{1}\) e \(F_{2}\) e suas respectivas tangentes, \(t_{1}\) e \(t_{2}\), são
$$
\begin{array}{ll}
F_{1}=\left( u\left( x,y_{0}\right) ,\ v\left( x,y_{0}\right) \right) ;\ &
t_{1}=\frac{\partial F_{1}}{\partial x}=\left. \left( u_{x},~v_{x}\right)
\right\vert _{\left( x_{0},y_{0}\right) },\; \; \\
F_{2}=\left( u\left( x_{0},y\right) ,~v\left( x_{0},y\right) \right) ;\ &
t_{2}=\frac{\partial F_{2}}{\partial y}=\left. \left( u_{y},~v_{y}\right)
\right\vert _{\left( x_{0},y_{0}\right) },
\end{array}
$$
lembrando que as tangentes são calculadas no ponto \(\left(x_{0},y_{0}\right)\). As tangentes são ortogonais, pois, tomando seu produto escalar obtemos
$$
t_{1}\cdot t_{2}=u_{x}u_{y}+v_{x}v_{y}=-u_{x}v_{x}+v_{x}u_{x}=0.
$$
Isto pode ser visualizado na figura abaixo.

Exemplo 14: Vamos visualizar a função \(w=\exp \left(z\right) =e^{z}\) como uma transformação e observar que as curvas \(\left( x_{\ },y_{0}\right)\) e \(\left( x_{0},y\right)\) no plano \(xy\) são levadas em curvas que se interceptam ortogonalmente no plano \(uv\). Notamos primeiramente que
$$
w=e^{x+iy}=e^{x}e^{iy}=e^{x}\left( \cos y+i\text{sen }y\right).
$$
As partes real e imaginária e suas derivadas são
$$
\begin{array}{lll}
u\left( x,y\right) =e^{x}\cos y, & u_{x}=e^{x}\cos y, & u_{y}=-e^{x}\text{sen }y, \\
v\left( x,y\right) =e^{x}\text{sen }y, & v_{x}=e^{x}\text{sen }y, & v_{y}=e^{x}\cos y.
\end{array}
$$
Como as condições de Cauchy-Riemann são satisfeitas e as derivadas parciais são contínuas a função é analítica. Além disto sua derivada é
$$
\frac{de^{z}}{dz}=\frac{\partial e^{z}}{\partial x}=\frac{\partial }{
\partial x}\left( e^{x+iy}\right) =e^{x+iy}=e^{z},
$$
e
$$
\vec{\nabla}u\cdot \vec{\nabla}v=u_{x}v_{x}+u_{y}v_{y}=0.
$$
A reta \(\left( x,~0\right)\) é levada em \(w=e^x\), que é a semi-reta \(u\gt 0,\; v=0\) do plano \(uv\). A reta \(\left( x,~\pi /4\right)\) é levada em \(w=e^{x}e^{i\pi /4}\), que é a semi-reta bissetriz do primeiro quadrante. A reta \(\left( 0,\ y\right)\) é levada em \(w=e^{iy}\), que é a circunferência de raio \(1\). Estas e outras retas de \(xy\) e sua imagem no plano \(uv\) estão representadas na figura. Observe que nenhum ponto de \(\mathbb{C}\) é levado na origem da imagem.

1. Encontre as partes real e imaginárias das seguintes funções:
$$
\begin{array}{ll}
\text{a) }\;\; w=z^{2}-5z+3 & \;\; \text{b) }\;\; w=\frac{z+2}{z-i} \\
\text{c) }\;\; w=e^{iz} & \;\; \text{d) }\;\; w=\sqrt{z}
\end{array}
$$
2. Qual é o domínio máximo de definição das seguintes funções?
$$
\begin{array}{ll}
\text{a)}\ f\left( z\right) =\frac{z}{x}-\frac{y}{z}\ \ \ \ \
& \text{b)}\ f\left( z\right) =\frac{z^{2}+\left( z-1\right) ^{3}}{\left(
e^{z}-1\right) \cos y}
\end{array}
$$
3. Mostre, usando a definição, que
$$
\frac{d}{dz}\left( \frac{1}{z}\right) =-\frac{1}{z^{2}}
$$
para \(z\neq 0\). Obtenha a mesma derivada usando
$$
\frac{d}{dz}\left( \frac{1}{z}\right) =\frac{\partial }{\partial x}\left(
\frac{1}{z}\right)
$$
na região onde \(f\) é analítica.
4. Calcule as derivadas de
$$
\begin{array}{ll}
\text{a)}\ f\left( z\right) =z^{5}+3iz^{2}-1\ \ \ \ \ & \text{b)
}\ f\left( z\right) =\left( z^{2}-1\right) ^{2}\left( iz+1\right) ^{3} \\
\text{c)}\ f\left( z\right) =\frac{z-1}{z-i} & \text{d)}\ f\left(
z\right) =ze^{iz}
\end{array}
$$
5. Mostre por indução que \(\left( z^{n}\right) ^{\prime }=nz^{n-1}\) para todo \(n\) inteiro positivo.
6. Verifique se são analíticas e, em caso afirmativo, em que região são analíticas e quais as derivadas das funções:
$$
\begin{array}{lll}
\text{a)}\;\;w=z^{3} & \text{b)}\;\;w=e^{y+ix} & \text{c)}\;\;w=\bar{z} \\
\text{d)}\;\;w=\sqrt{z} & \text{e)}\;\;w=e^{-z} & \text{f)}\;\;w=x+iy\; \text{ a identidade.}
\end{array}
$$
7. Dadas as funções
$$
\text{(a)}\;\; w=z^{2}\;\; \text{(b)}\;\; w=\frac{1}{z}
$$
faça os gráficos das famílias de curvas \(\ u\left( x,y\right)=c_{1}\) e\ \(v\left( x,y\right) =c_{2}\) e verifique se elas se cruzam ortogonalmente.
<h3Logaritmo
Embora já tenhamos usado o logaritmo em um exercício para mostrar que é uma função analítica em \(\mathbb{C}\) será útil fazermos um estudo mais completo desta função. Como uma revisão nos lembraremos de que o logaritmo natural ou neperiano pode ser definido como a área sob a curva do hipérbole \(y=1/t\), como ilustrado na figura.

Como consequência temos as propriedades:
Uma das motivações que levaram ao estudo dos números complexos foi exatamente a necessidade de se atribuir algum sentido ao logaritmo de números negativos, que não está definido para os reais. Como veremos a extensão desta função para os complexos está definida em \(\mathbb{C}-\left\{ 0\right\}\). Esta extensão é obtida de modo muito natural escrevendo-se
$$
\ln z=\ln re^{i\theta }=\ln r+\ln e^{i\theta }=\ln r+i\theta ,
$$
lembrando que a parte real está bem definida se \(z\neq 0\) pois, neste caso, \(r=\left\vert z\right\vert >0\). Se \(z\) é real então \(\theta =0\) e \(\ln z=\ln r\) e o logaritmo coincide com a função real. Com esta definição podemos dar um sentido ao logaritmo de um número negativo. Um exemplo disto é a célebre identidade escrita por Euler “associando os 4 números mais importantes”,
$$
e^{i\pi }=-1\Rightarrow \ln \left( -1\right) =i\pi .
$$
Observe, no entanto, que definida desta forma a função tem um problema. Ela é uma função “multivalente” , isto é, o mesmo ponto \(z\) pode corresponder a diversos pontos na imagem, o que não é compatível com a definição usual de uma função. Isto ocorre por uma ambiguidade na forma de se expressar o ponto \(z\), no domínio da função. Um ponto pode ser escrito como
$$
z=re^{i\theta }=re^{i\left( \theta +2k\pi \right) },\ k=0,~\pm 1,~\pm 2,…
$$
que pode ser levado em diversos pontos da imagem,
$$
\ln z=\ln re^{i\left( \theta +2k\pi \right) }=\ln r+i\left( \theta +2k\pi
\right) ,\ k\in \mathbb{Z}.
$$
Para torná-la uma função “univalente” podemos proceder da seguinte forma: para qualquer valor do argumento \(\theta\) em \(z=re^{i\theta }=re^{i\left( \theta+2k\pi \right) }\) tomamos \(\theta _{0}\) como o valor do argumento no intervalo \(\left[ 0,~2\pi \right)\). Então
$$
\theta _{0}=\theta +2k\pi ,\ k\in \mathbb{Z}
$$
e definimos o ramo principal (ou determinação) do \(\ln\) como \(\ln \theta =\ln \theta _{0}\). Se restringirmos \(\arg \left( z\right)\) aos intervalos
$$
2k\pi \leq \theta \lt 2\left( k+1\right) \pi ,\ k\in \mathbb{Z}
$$
teremos para cada valor de \(k\) um ramo do \(\ln\), ou seja
$$
\ln _{k}z=\ln r+i\theta .
$$
O logaritmo fica, desta forma, univocamente determinado se informarmos o ramo que está sendo usado. Os pontos \(\theta =0\) representam uma reta de corte em \(\mathbb{C}\), representada na figura (a) e são chamados pontos de ramificação. Pode ser interessante, dependendo da aplicação, estabelecer outra reta de corte definindo ramos diferentes para o \(\ln\). Podemos tomar
$$
\alpha \leq \theta \lt \alpha +2 \pi \;\;\text{ ou }\;\; \alpha \lt \theta \leq \alpha +2\pi,
$$
como representado na figura (b). Ao tomar estas restrições dizemos que \(\mathbb{C}\) foi cortado ao longo de \(z=re^{i\alpha }\).

Como já visto o logaritmo é analítico em \(z\neq 0\) no ramo principal, conclusão que pode ser ampliada para qualquer ramo. Por outro lado, usando a regra da cadeia, obtemos sua derivada,
$$
\frac{d}{dz}\ln \left( z\right) =\frac{\partial }{\partial x}\ln \left(z\right) =\frac{\partial }{\partial x}\left( \ln r+i\theta \right)
=\left(\frac{\partial r}{\partial x}\frac{\partial }{\partial r}+\frac{\partial\theta }{\partial x}\frac{\partial }{\partial \theta }\right)
\left( \ln r+i\theta \right),
$$
e as derivadas \(r_x=\cos \theta,\;\; r_y=-\text{sen }\theta /r\)
$$
\frac{d}{dz}\ln \left( z\right) =\left( \frac{\partial r}{\partial x}\frac{\partial }{\partial r}+\frac{\partial \theta }{\partial x}\frac{\partial }{\partial \theta }\right) \left( \ln r+i\theta \right) =\left( \frac{1}{r}\frac{\partial r}{\partial x}+i\frac{\partial \theta }{\partial x}\right) =
$$
$$
=\frac{\cos \theta }{r}-i\frac{\text{sen }\theta }{r}=\frac{e^{-i\theta }}{r}=\frac{1}{re^{i\theta }}=\frac{1}{z}.
$$
Um maneira prática de se visualizar o efeito da função logaritmo, e de outras funções igualmente, é encará-la como uma transformação entre pontos de \(\mathbb{C}\). Na tabela seguinte estão listados alguns conjuntos de pontos no domínio e sua imagem pelo logaritmo.
$$
\begin{array}{lll}
\text{Imagem } & z & \text{Domínio, } f\left( z\right) \\
\text{ponto } & z=0 & \ln 0=1 \\
\text{ponto } & z=i & \ln \left( i\right) =i\pi /2 \\
\text{reta } & \theta = cte. & v=\theta \left( \text{reta}\right) \\
\text{círculo } & r=1 & u=0\; \text{ (reta)} \\
\text{círculo } & r \gt 1 & u= \text{ cte. positivo (reta.)}
\end{array}
$$
Cada ramo tem como imagem uma faixa no plano \(w\), satisfazendo \(-\infty\lt u\lt \infty,\;\; 0\leq v \lt 2\pi\). A totalidade dos ramos cobre o plano \(w\). Observe na figura que retas \(\theta =\) cte. no plano \(z\) são levadas em \(w=\ln r+i\theta\) no plano \(w\), que são retas \(u=\) cte., enquanto circunferências \(r=\) cte. são levadas nas retas \(v=\) cte.no plano \(w\). A circunferência \(r=1\) tem como imagem a reta \(u=0\) (o eixo \(\mathcal{O}v)\) enquanto circunferências com raios menores (maiores) que 1 são levadas em retas verticais à esquerda (direita) do eixo \(\mathcal{O}v\).

Observe as funções exponencial e logaritmo são inversas mútuas: tome
$$
w=\ln _{k}z=\ln r+i\left( \theta +2k\pi \right) ,\ k=0,1,2,…
$$
Então, tomando a exponencial deste último termo temos
$$
e^{w}=e^{\ln _{k}z}=e^{\left[ \ln r+i\left( \theta +2k\pi \right) \right]
}=re^{i\left( \theta +2k\pi \right) }=re^{i\theta }=z.
$$
Por outro lado
$$
\ln _{k}\left( e^{w}\right) =\ln _{k}e^{\left[ \ln r+i\left( \theta +2k\pi\right) \right] }
=\ln _{k}\left( re^{i\theta }\right) =\left[ \ln r+i\left(\theta +2k\pi \right) \right] =w,
$$
como foi afirmado. Outras propriedades adicionais do logaritmo são:
A partir da equação de Euler e seu conjugado complexo
$$
\begin{array}{l}
e^{iy}=\cos y+i\text{sen }y \\
e^{-iy}=\cos y-i\text{sen }y
\end{array}
$$
podemos verificar que as funções trigonométricas seno e cosseno podem ser escritas como
$$\begin{array}{l}
\cos y=\frac{1}{2}\left( e^{iy}+e^{-iy}\right), \\
\text{sen }y=\frac{1}{2i}\left( e^{iy}-e^{-iy}\right),
\end{array}
$$
definidas apenas para valores reais de \(y\). Podemos extender as funções para ter validade sobre todo o plano complexo fazendo
$$
\cos z=\frac{1}{2}\left( e^{iz}+e^{-iz}\right) ,
$$
$$
\text{sen }z=\frac{1}{2i}\left( e^{iz}-e^{-iz}\right).
$$
De forma análoga definimos
$$
\text{tag}z=\frac{\text{sen }z}{\cos z},\ \text{cotg}z=\frac{\cos z}{\text{sen }z},\ \sec z=\frac{1}{\cos z},\ \csc z=\frac{1}{\text{sen }z},
$$
respectivamente a tangente, cotangente, secante e cossecante. As derivadas das funções continuam formalmente iguais as derivadas no eixo real:
$$
\left( \text{sen }z\right) ^{\prime }=\cos z,\ \left( \cos z\right)^{\prime }=-\text{sen }z,
$$
como pode ser facilmente verificado derivando-se as expressões em (3). Da mesma forma se verifica que
$$
\begin{array}{l}
\text{sen }\left( -z\right) =-\text{sen }z,\ \ \cos \left( -z\right) =\cos z, \\
\text{sen }^{2}z+\cos ^{2}z=1, \\
\text{sen }\left( z_{1}+z_{2}\right) =\text{sen }z_{1}\cos z_{2}+\cos z_{1}\text{sen }z_{2}, \\
\cos \left( z_{1}+z_{2}\right) =\cos z_{1}\cos z_{2}-\text{sen }z_{1}\text{sen }z_{2}, \\
\text{sen }z=\cos \left( \frac{\pi }{2}-z\right) ;\ \ \cos z=\text{sen }\left( \frac{\pi }{2}-z\right).
\end{array}
$$
As funções hiperbólicas são extendidas para o plano complexo através das definições:
$$
\text{senh}z=\frac{1}{2}\left( e^{z}-e^{-z}\right) ,
$$
$$
\cosh z=\frac{1}{2}\left( e^{z}+e^{-z}\right).
$$
Com estas definições valem
$$
\left( \text{senh }z\right) ^{\prime }=\cosh z;\ \ \left( \cosh z\right) ^{\prime }=\text{senh}z.
$$
Exercícios :
1. Mostre que \(\ln \left( -1\right) =\left( 2k+1\right) \pi i\) e \(\ln \left(i\right) =\left( \frac{4k+1}{2}\right) \pi i,~k=0,\pm 1,\pm 2,…\).
2. Mostre que, se \(x\neq 0\),
$$
\ln \left( x+iy\right) =\frac{1}{2}\ln \left( x^{2}+y^{2}\right) +i\left(
\theta _{0}+2k\pi \right) ,
$$
onde \(\theta _{0}\) é uma das determinações de \(\text{arctg}\left( y/x\right)\).
3. Determine as raízes de
$$
\begin{array}{lll}
\text{(a)}\ e^{z}=-1, & & \text{(b)}\ e^{2z}=-e, \\
\text{(c)}\ e^{z}=-\sqrt{3}+3i, & & \text{(d)}\ \ln z=\pi i/2, \\
\text{(e)}\ e^{z}+6e^{-z}=5, & & \text{(f)}\ e^{3z-4}=-1.
\end{array}
$$
4. Mostre as seguintes relações:
$$
\begin{array}{lll}
\text{(a)}\ \left( \text{sen }z\right) ^{\prime }=\cos z, & \text{(b)}\
\left( \cos z\right) ^{\prime }=-\text{sen }z, & \text{(c)}\ \text{sen }^{2}z+\cos ^{2}z=1, \\
\text{(d)}\ \left( \text{senh}z\right) ^{\prime }=\cosh z, & \text{(e)}\ \left( \cosh z\right) ^{\prime }=\text{senh}z, & \text{(f)}\ \text{sen }\left( iz\right) =i\text{senh }z, \\
\text{(g)}\ \cos \left( iz\right) =\cosh z, & \text{(h)}\ \cosh ^{2}z-\text{senh}^{2}z=1, & \text{(i)}\ \text{senh}\left( z+i\pi \right) =-
\text{senh}z, \\
\text{(j)}\ \cosh \left( z+i\pi \right) =-\cosh z, & \text{(k)}\;\; \cos \left(x+iy\right) =\cos x\cosh y-i\text{sen }x\text{ senh }y.&
\end{array}
$$