Desafios
O Problema de Monty Hall
A televisão americana manteve por muitos anos um programa chamado Let’s make a deal! (Vamos negociar). Nele o apresentador (que era o canadense Monty Hall) apresentava três portas fechadas para um concorrente. Em uma delas havia um automóvel, nas duas outras uma cabra. O concorrente ganharia o automóvel se escolhesse a porta com o automóvel. Uma vez escolhida uma das portas Hall abria outra porta entre as restantes, onde havia uma cabra, e perguntava ao concorrente se ele queria trocar de portas. O que você deve fazer para ter maior chance de ganhar o automóvel?
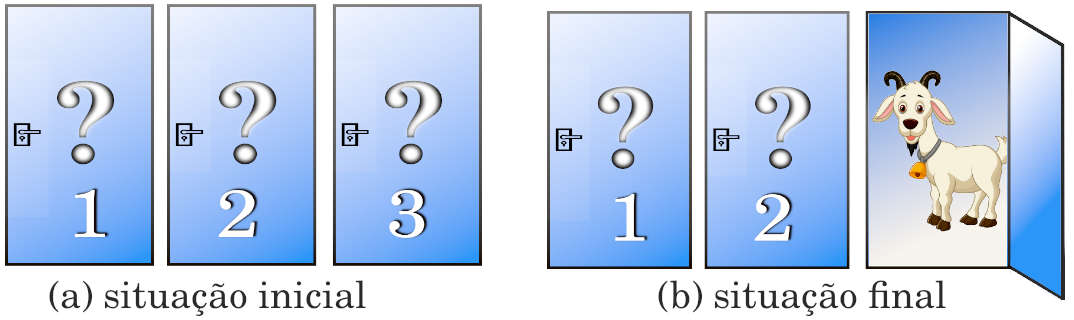
Sem perda de generalidade, vamos supor que você tenha escolhido a porta nº 1. O anfitrião do programa então abre a porta nº 3, que tem uma cabra. E diz: “Você quer trocar para a porta nº 2?”
É vantajoso mudar de escolha?
A solução do problema foi enviada por Steve Selvin para a revista American Statistician em 1975. Houve muito debate sobre o tema e ainda hoje se encontra pessoas que negam essa solução.Na primeira escolha (situação a) o concorrente podia escolher uma porta entre três, uma delas premiada. Logo ele tinha 1/3 de chances de acertar, 2/3 de errar.
Na segunda escolha (situação b) uma informação a mais foi inserido, a de que a porta nº 3 escondia uma cabra. O concorrente pode agora escolher uma porta entre duas. Logo ele tem agora 1/2 de chance de acertar, 1/2 de errar. Ele deve portanto mudar a sua escolha.
Muitos estatísticos se recusaram (e ainda se recusam) a aceitar essa solução e sua explicação, embora provas formais tenham sido desenvolvidas para mostrar isso. Conta-se que até Paul Erdös, um dos matemáticos modernos mais prolíficos, se recusou a aceitá-la até ver uma simulação de computador que mostra que essa é a escolha correta.
Encontre a Jóia Falsa
Você tem em mãos 9 pedras do mesmo tamanho e mesma aparência. Todas são diamantes, exceto uma delas, constituída de material mais leve. Você tem uma balança de pratos (que apenas serve para comparar pesos).
Como encontrar a pedra falsa fazendo apenas 2 pesagens?
Separe as pedras em 3 grupos de 3 pedras cada. Tome 2 desses grupos de 3 pedras e compare seus pesos. Se o peso for igual a pedra mais leve, portanto falsa, está no grupo isolado, fora da balança. Caso contrário ela está no grupo mais leve na balança. Usando o grupo mais leve compare o peso de 2 de suas pedras, deixando a terceira de fora e repita o mesmo procedimento!
Mais uma na Balança
Você recebe um carregamento de 10 caixas. Em cada caixa há 10 objetos pesando 10 gramas cada, exceto por uma delas onde, por defeito na fabricação, todos os objetos pesam, cada um, 1g a mais que os das outras caixas. O único instrumento disponível é uma balança graduada onde é possível ler o peso.
Como descobrir a caixa com os objetos defeituosos fazendo uma única medida?
Coloque as caixas em ordem, tome 1 objeto da primeira caixa, 2 da segunda, e asssim consecutivamente, até colocar todos os 10 objetos da 10ª caixa na balança. Se todos os objetos tivessem o mesmo peso (de 10g) a balança acusaria um peso de
10g + 20g + 30g + 40g + 50g + 60g + 70g + 80g + 90g + 100g = 550 gramas.
Se houver peso extra de 1g na medida (ou seja, se o peso total for de 551 g) a 1ª caixa contém os objetos defeituosos, 2g para 2ª caixa, … , 10g para 10ª caixa.
Os olhos azuis na Ilha
Um problema de lógica razoavelmente difícil.
Este é um problema bem definido e com solução lógica. Não é uma pegadinha nem um jogo de palavras.
200 pessoas moram em uma ilha, 100 com olhos azuis, 100 com olhos castanhos e uma guru, com olhos verdes. Ninguém na ilha sabe a cor de seus próprios olhos, não pode olhar em espelhos nem contar um ao outro qual é esta cor. Todos são excelentes lógicos – se uma conclusão pode ser deduzida logicamente eles o farão imediatamente. Todos podem ver os olhos dos demais moradores a qualquer momento e podem contar quantas pessoas têm olhos de cada cor.
Uma pessoa de olhos azuis pode ver 100 pessoas com olhos castanhos e 99 pessoas com olhos azuis (e uma com verde, a guru), mas isso não permite que ele saiba a cor de seus próprios olhos; para ele podem existir 101 pessoas de olhos castanhos e 99 de olhos azuis. Ou ele poderia até ter olhos verdes ou pretos!
Todas as noites um barco pára na ilha e qualquer morador que descobrir a cor de seus olhos deixará a ilha. Todos conhecem as regras aqui listadas.
Um dia, antes que chegue o barco, a guru anuncia para todos:
Posso ver alguém de olhos azuis.
Quem deixa a ilha, e em que noite?
Suponha que exista na ilha apenas uma pessoa de olhos azuis. O número de pessoas com olhos de outra cor não é relevante. Com o pronunciamento da guru ela saberia imediatamente que tem olhos azuis e sairia da ilha no mesmo dia. Se houver 2 pessoas de olhos azuis, cada uma delas perceberá que a outra não saiu no primeiro dia (porque enxergou outra pessoa com olhos azuis) e então ambas sairão no segundo dia. Pelo mesmo raciocínio se conclui que as 100 pessoas da ilha sairão no
centésimo dia.
O Teste de Wason
O teste de Wason foi usado para testar competência de seus sujeitos (as pessoas testadas). No estudo original, feito em 1966, apenas 10% dos testados acertavam a resposta. Quatro cartas estão dispostas em uma mesa à sua frente mostrando A, 7, D e 4.
Você recebe a informação de que cada uma delas contém uma letra em uma face, um dígito na outra. Você deve verificar a seguinte hipótese: todas as cartas que contém uma vogal contém um número par. Quais cartas devem ser viradas para verificar a hipótese?
A resposta correta é que você só precisa virar as cartas com A e 7. Deve haver um número par na primeira e uma consoante na segunda, caso contrário a hipótese está incorreta. Os reversos das cartas com D e 4 são irrelevantes, pois nada têm a ver com a hipótese formulada. Apenas as duas primeiras cartas podem falsear a hipótese e as duas últimas não servem para testá-la.
A maioria das pessoas decide olhar as quatro cartas pois, instintivamente procuram por evidências que confirmem sua suposição. Mas um teste mais eficaz consiste em tentar provar que a suposição é falsa. Se não for possível, então ela deve ser verdadeira.
Leia mais sobre o
Viés de Confirmação e Teste de Wason.
Os três cavalos mais rápidos
Você tem 25 cavalos e precisa descobrir quais são os 3 mais rápidos entre eles. Para isso você pode fazer testes de comparação colocando 5 cavalos de cada vez para competir em uma corrida. Você verá a ordem de classificação, mas não o tempo ou velocidade de cada um.
Qual é o menor número de testes necessários para fazer a sua seleção?
É possível selecionar os três mais rápidos com 7 testes ou corridas.
Comece por dividir os cavalos em cinco grupos e realizando 5 corridas. Como na figura, coloque cada grupo em uma linha em ordem de sua velocidade. Vamos denominar essas linhas como a, b, c, d, e. Chamaremos as colunas de 5, 4, 3, 2, 1, sendo que a coluna 1 tem os cavalos mais rápidos e a coluna 5 os mais lentos.
Depois faça o 6º teste com os cavalos da coluna 1 e os reordene (inclusive alterando as linhas a que cada cavalo pertence) colocando em cima o mais rápido de todos. Portanto o cavalo a1 é o vencedor de todos, um de nossos 3 cavalos procurados. Para encontrar os outros 2 vamos excluir o maior número possível de cavalos.
Olhando na figura, estão excluídos e marcados com um X branco:
todos os cavalos das colunas 4 e 5 podem ser excluídos pois, na melhor das hipóteses, são o 4º e 5º mais rápidos de suas linhas.
Cavalos d1 e e1 também são 4º e 5º da coluna 1. Como temos que encontrar apenas 2, os cavalos b3, c3, d3, e3 também podem ser excluídos (pois são, no máximo, os terceiros colocados).
Marcados com um X vermelho estão:
c2, porque é mais lento que c1 (que é no máximo 3º),
d2 mais lento que d1,
e2 mais lento que e1 (ambos já excluidos).
Restam 5 cavalos que podem ser selecionados com apenas 1 teste adicional. Logo precisamos de 7 testes.
Enquanto os colegas faziam as contas: 1 + 2 + 3 + . . . . + 99 + 100 = S, Gauss agrupou os inteiros em duas colunas e depois somou os números em cada linha:Vemos que Gauss obteve 50 linhas cuja soma é 101. A soma total é, portanto, 50 × 101 = 5050.
