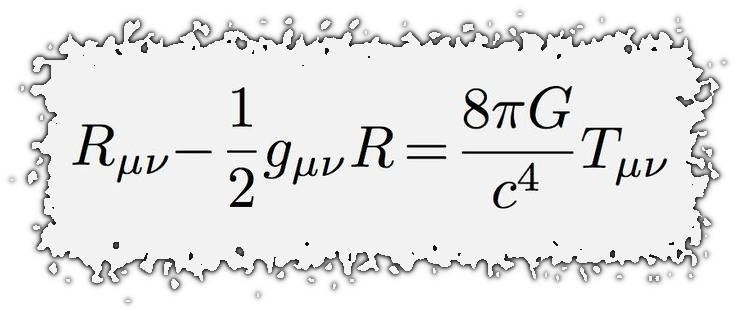Até o momento discutimos o movimento de partículas livres e a transformação de seu movimento entre dois referenciais inerciais. Partículas livres descrevem retas em \(M_4\) e estas retas são levadas em outras retas por meio de transformações de Lorentz, já que elas são transformações lineares. Concluímos que, assim como acontece na mecânica clássica sob transformações de Galileu, a inércia não fica alterada de um referencial para outro. Qualquer desvio na linearidade do movimento de uma partícula deve ser atribuído à presença de alguma interação, uma força agindo sobre ela.

Para construir uma dinâmica devemos definir massa e momento sobre esta teoria. Na teoria Newtoniana a massa é uma constante de proporcionalidade entre a aceleração e a força. Na TRE tentamos seguir de perto, tanto quanto possível, as definições e conceitos da mecânica clássica, principalmente tendo em mente que a teoria relativística deve se reduzir à clássica no caso limite de baixas velocidades, em particular no que se refere às leis de conservação.

Construímos, na seção anterior, os quadrivetores
$$
u^{\mu} = \frac{dx^{\mu}}{d \tau} = \left( \gamma c, \gamma v \right), \text{} p^{\mu} = mu^{\mu} = \left( \gamma mc, \gamma mv \right) .
$$

Vimos que as partes espaciais destes quadrivetores se relacionam com a velocidade e o momento linear ordinários em 3 dimensões de forma simples,
$$
u_{\left( 4 \right)}^i = \gamma v_{\left( 3 \right)}^i ; p_{\left( 4
\right)}^i = \gamma p_{\left( 3 \right)}^i .
$$

Gostaríamos agora de explorar um pouco mais o significado do componente temporal \(p^0\) do quadrivetor momento, o que faremos na próxima seção, juntamente com o conceito de força generalizada.

Além dos vetores \(u^{\mu}\) e \(p^{\mu}\) , contruídos à partir da linha mundo \(x^{\mu} \left( \tau \right)\) , podemos definir um terceiro vetor
interessante
$$
K^{\mu} = m \frac{d^2 x^{\mu}}{d \tau} = \frac{dp^{\mu}}{d \tau} =
\frac{d}{d \tau} \left( \gamma mc, \gamma mv \right) .
$$

a chamada força generalizada de Minkowsky.\(\mathbb{}\) Denotaremos o componente espacial desta força de \(\vec{F}\) e portanto \(K = \left( K^0, \vec{F} \right)\). Em particular estamos interessados em descobrir as quantidades que se conservam nesta teoria.

Contraindo a força generalizada e a 4-velocidade podemos obter um esclarecimento sobre \ natureza do componente \(p^0\) do momento. Começamos
por notar que
$$
u^{\mu} K_{\mu} = mu^{\mu} \frac{du_{\mu}}{d \tau} = 0.
$$

A expressão acima se anula pois
$$
0 = \frac{d}{d \tau} \left( u_{\mu} u^{\mu} \right) = u_{\mu}
\frac{du^{\mu}}{d \tau} = \left( \frac{du_{\mu}}{d \tau} \right) u^{\mu} =
2 u_{\mu} \frac{du^{\mu}}{d \tau},
$$

já que \(u_{\mu} u^{\mu} = – c^2\) é uma constante. Observe também que usamos neste cálculo o fato de que \(\eta_{\mu \nu}\) é formado por constantes e portanto
$$
u^{\mu} \frac{du_{\mu}}{d \tau} = u^{\mu} \frac{d \left( \eta_{\mu \nu}
u^{\nu} \right)}{d \tau} = \eta_{\mu \nu} u^{\mu} \frac{du^{\nu}}{d \tau}
= u_{\mu} \frac{du^{\mu}}{d \tau} .
$$

Por outro lado
$$
0 = u^{\mu} K_{\mu} = – \left( u^0 K^0 \right) + u^i K_i = – \gamma cK^0 +
\gamma v^i K_i,
$$

de onde tiramos uma expressão para \(K^0\) ,
$$
K^0 = \frac{1}{c} v^i K_i = \frac{1}{c} \vec{v} . \vec{F} .
$$

Prosseguindo na analogia com o caso clássico relembramos a equação 2. Se \(T\) é a energia cinética de uma partícula então
$$
\frac{dT}{dt} = \vec{F} . \vec{v},
$$

o que sugere a adoção da seguinte notação: fazemos
$$
P^0 = \gamma mc = \frac{E}{c}
$$

e, por conseguinte,
$$
K^0 = \frac{1}{c} \frac{dE}{d \tau},
$$

onde \(E\) é a energia total da partícula, cujo sentido exploraremos em seguida. Usando estas definições temos

$$
E = \gamma mc^2 \text{e} \vec{p} = \gamma m \vec{v}, \label{emc2}
$$
generalizações da energia e do momento ordinário, podemos escrever o vetor quadri-momento como

$$
p^{\mu} = \left( \frac{E}{c}, \vec{p} \right) . \label{pmu}
$$
A norma deste vetor é invariante,
$$
p^{\mu} p_{\mu} = – \left( \frac{E}{c} \right)^2 + p^2 = – m^2 c^2,
$$

sendo \(p = \left| \vec{p} \right|\). Uma expressão útil pode ser obtida daí,
$$
E^2 = m^2 c^4 + p^2 c^2,
$$

uma expressão que associa a energia total da partícula com sua massa e velocidade. No referencial comóvel, onde \(\gamma = 1\) e \(p = 0\) temos a famosa equação de Einstein
$$
E = mc^2,
$$

válida, como já indicado, apenas no referencial da partícula. Outra relação interessante pode ser obtida para o caso de baixas velocidades, \(\beta \ll 1\). Neste caso usamos a expansão em séries de potências mantendo apenas os termos mais relevantes para escrever \(\gamma \approx \left( 1 + \beta^2 / 2 \right)\) e a equação 7 para a energia se torna
$$
E = \gamma mc^2 \approx \left( 1 + \frac{\beta^2}{2} \right) mc^2 = mc^2 +
\frac{1}{2} mv^2 .
$$

Para baixas velocidades a energia definida na equação 7 é a energia cinética ordinária mais um termo constante que denominaremos energia de repouso da partícula.

Diversos fenômenos observados confirmam a correção destas expressões. Um exemplo interessante é o da aniquilação de um elétron e um pósitron que resulta na completa aniquilação da massa de repouso das partículas iniciais resultando na emissão de fótons com massa de repouso nula que transportam toda a energia inicial do sistema. Reações atômicas que ocorrem dentro de reatores nucleares ou bombas atômicas se utilizam da fissão nuclear, a quebra de núcleos, para a liberação de grandes quantidades de energia. Os núcleos partidos possuem massa menor que a massa inicial, a diferença sendo liberada sob forma de energia transportada por radiação eletromagnética. Um processo análogo, porém inverso, ocorre no interior das estrelas onde núcleos leves, basicamente hidrogênio e hélio, são fundidos em núcleos mais pesados, resultando na liberação de energia.

Leis de conservação

Na Mecânica Clássica as simetrias do sistema considerado levam às leis de conservação. Um sistema homogêneo por translações de coordenadas exibe conservação do momento linear enquanto sistemas isotrópicos apresentam conservação do momento angular. Se um sistema é homogêneo por translaçãoes temporais então ele possue a energia total conservada.

Na Teoria da Relatividade Especial os escalares são as quantidades conservadas. Escalares são invariantes quando se troca de um sistema de coordenada estabelecido em um referencial inercial para outro sistema inercial. Em um referencial comóvel uma partícula tem o 4-momento
$$
p^{\mu} = \left( m_0 c, \vec{0} \right),
$$

onde \(m_0\) é a chamada massa de repouso da partícula, a massa medida por um observador no referencial comóvel. Calculamos \(p^{\prime \mu}\) obtido por meio de uma transformação de Lorentz sobre o momento anterior
$$
p^{\prime \mu} = \Lambda_{\hspace{0.75em} \alpha}^{\mu} p^{\alpha} = \left[
\begin{array}{cccc}
\gamma & \gamma v / c & \hspace{0.75em} 0 & \hspace{0.75em} 0\\
\gamma v / c & \gamma & \hspace{0.75em} 0 & \hspace{0.75em} 0\\
0 & 0 & \hspace{0.75em} 1 & \hspace{0.75em} 0\\
0 & 0 & \hspace{0.75em} 0 & \hspace{0.75em} 1
\end{array} \right] \left[ \begin{array}{c}
m_0 c\\
0\\
0\\
0
\end{array} \right] = \left[ \begin{array}{c}
\gamma m_0 c\\
\gamma m_0 v\\
0\\
0
\end{array} \right],
$$

ou seja,
$$
p^{\prime \mu} = \gamma \left( m_0 c, \hspace{0.25em} m_0 v
\hspace{0.25em}, 0 \hspace{0.25em}, 0 \right) .
$$

Se pretendemos manter a expressão para o momento como composto por energia e momento, \(p^{\mu} = \left( \frac{E}{C}, \hspace{0.75em} m \mathbf{v} \right)\) teremos então que definir
$$
m = \gamma m_0 = \frac{m_0}{\sqrt{1 – \beta^2}}
$$

que mostra a dilatação da massa para partículas em altas velocidades. Nenhum objeto com massa de repouso não nula pode ser acelerado até uma velocidade igual ou superior à velocidade da luz.

Podemos mostrar que, na TRE, o quadrivetor momento-energia é uma entidade conservada em um sistema de partículas. Definindo a variação total de momento-energia em um referencial como
$$
\Delta p^{\mu} = \left( \sum^n_a p_a^{\mu} \right)_{final} – \left(
\sum^n_a p_a^{\mu} \right)_{inicial}
$$

onde a soma é realizada sobre todas as partículas do sistema. Em outro referencial os momentos são transformados, para cada partícula, da seguinte forma
$$
p_a^{\prime \mu} = \Lambda_{\nu}^{\mu} p_a^{\nu}
$$

e, portanto, a variação total do momento-energia é
$$
\Delta p^{\prime \mu} = \left( \sum^n_a \Lambda_{\nu}^{\mu} p_a^{\nu}
\right)_{final} – \left( \sum^n_a \Lambda_{\nu}^{\mu} p_a^{\nu}
\right)_{inicial} = \Lambda_{\nu}^{\mu} \Delta p^{\nu} = \Delta p^{\mu} .
$$

Isto significa que se a variação total é nula em um referencial então ela será nula em qualquer referencial inercial. Observe que, para concluir isto, seria suficiente afirmar que a variação total, sendo composta por somas de vetores, é também um vetor. Se transformarmos este vetor para o referencial comóvel os componentes de \(\mathbf{p}\) são, como vimos na equação 8, a energia e o momento ordinário, ambos quantidades conservadas em qualquer reação ou interação de forma que a variação total do sistema será \(\Delta p^{\prime \mu} = 0\). Concluimos assim que
$$
\Delta p^{\mu} = 0
$$

em qualquer referencial inercial. Note, no entanto, que o momento e a energia não se conservam isoladamente.

Convenções e notação

O espaço-tempo é denominado \(M_4\) , o espaço de Minkowsky, cujos pontos são os eventos
$$
\mathbf{x =} \left( x^0, x^1, x^2, x^3 \right) \text{ ou, resumidamente, }
\mathbf{x =} \left\{ x^{\mu} \right\} .
$$

Vetores de \(M_4\) são representados por letras em negrito, \(\mathbf{x, u, p}\) enquanto vetores de \(I \hspace{-4pt} R^3\) são representados por meio de setas \(\vec{x} = \left( x, y, z \right)\) ou \(\vec{x} = \left\{ x^i \right\}\).Algumas vêzes é interessante separar o vetor em suas partes temporal e espacial fazendo, por exemplo,
$$
\mathbf{p} = \left( p^0, \vec{p} \right)
$$

Usamos índices gregos como índices do espaço-tempo,
$$
\alpha, \beta, \mu, \nu = 0, 1, 2, 3,
$$

enquanto índices latinos são puramente espaciais:
$$
i, j, k = 1, 2, 3.
$$

\(\left\{ \mathbf{\hat{e}}_{\mu} \right\}\) é a base canônica de \(M_4\), onde \(\mathbf{\hat{e}}_0\) é um vetor unitário puramente temporal e \(\mathbf{\hat{e}}_1 = \hat{\imath}, \mathbf{\hat{e}}_2 = \hat{\jmath}, \mathbf{\hat{e}}_3 = \hat{k}\).A métrica de Minkowsky é \(\eta_{\mu \nu} = \textit{diag} \left( -, +, +, + \right)\). A base canônica \(\left\{ \mathbf{\hat{e}}_{\mu} \right\}\) é ortonormal em relação à métrica de Minkowsky, ou seja

$$
\mathbf{\eta} \left( \mathbf{\hat{e}}_0, \mathbf{\hat{e}}_0 \right) = – 1,
$$

$$
\mathbf{\eta} \left( \mathbf{\hat{e}}_i, \mathbf{\hat{e}}_j \right) = \delta_{ij} .
$$

A convenção de Einstein para o somatório, onde índices repetidos são somados, é adotada em quase todo o texto. Com ela podemos escrever, por exemplo,

$$
ds^2 = \sum^3_{\mu, \nu = 0} dx^{\mu} dx^{\nu} \eta_{\mu \nu} = dx^{\mu}
dx^{\nu} \eta_{\mu \nu} .
$$

Bibliografia

• Carrol, Sean, M.: Lecture Notes in General Relativity, gr-qc/9712019, Santa Barbara, 1997.
• Lopes, J. L.: A Estrutura Quântica da Matéria, Editora UFRJ, Rio e Janeiro, 1993.
• Misner, C., Thorne, K., Wheeler, A.: Gravitation, W. H. Freeman and Co., San Francisco, 1970.
• Ohanian, H., Ruffini: Gravitation and Spacetime, W. W. Norton & Company, New York, 1994.
• Ramond, P.: Field Theory, A Modern Primer, Addison-Wesley, New York, 1990.
• Weinberg, S.: Gravitation and Cosmology, Principles and Applications of General Theory of Relativity, John Wiley and Sons, New York, 1971.

Início: TRE

O espaço onde os fenômenos ocorrem, segundo a TRE, é um espaço vetorial de quatro dimensões que denotaremos por \(M_4\), o espaço de Minkowsky (que é similar ao \(R^4\), mas não euclidiano, como veremos). Cada ponto deste espaço é denominado um evento e será marcado com as coordenadas \((ct, \hspace{0.25em} x, \hspace{0.25em} y, \hspace{0.25em} z)\) que descrevem quando e onde o evento ocorreu. Cada ponto, portanto, pode ser associado a um quadrivetor \(\mathbf{x} = \left\{ x^{\mu} \right\} = \left( ct, \hspace{0.25em} x, \hspace{0.25em} y, \hspace{0.25em} z \right)\).

Com esta definição podemos reescrever a separação infinitesimal na forma
$$
ds^2 = – c^2 dt^2 + dx^2 + dy^2 + dz^2 = – \left( dx^0 \right)^2 + \left(
dx^1 \right)^2 + \left( dx^2 \right)^2 + \left( dx^3 \right)^2 = \eta_{\mu
\nu} dx^{\mu} dx^{\nu}
$$

onde escrevemos

$$
\eta_{\mu \nu} = \left( \begin{array}{cccc}
– 1 & 0 & 0 & 0\\
\hspace{0.75em} 0 & 1 & 0 & 0\\
\hspace{0.75em} 0 & 0 & 1 & 0\\
\hspace{0.75em} 0 & 0 & 0 & 1
\end{array} \right) . \label{etaMikowsky}
$$
Por construção as transformações de Lorentz deixam invariante este intervalo. Estas transformações, dadas pelas equações 5, podem ser escrita da seguinte forma:
$$
x^{\prime 0} = \gamma \left( x^0 – \frac{v}{c} x^1 \right),
\hspace{1.5em} x^{\prime 2} = x^2
$$

$$
x^{\prime 1} = \gamma \left( x^1 – \frac{v}{c} x^0 \right), \hspace{1.5em} x^{\prime 3} = x^3 .
$$

Em forma matricial temos
$$
\left[ \begin{array}{c}
x^{\prime 0}\\
x^{\prime 1}\\
x^{\prime 2}\\
x^{\prime 3}
\end{array} \right] = \left[ \begin{array}{cccc}
\gamma & – \gamma v / c & \hspace{0.75em} 0 & \hspace{0.75em} 0\\
– \gamma v / c & \gamma & \hspace{0.75em} 0 & \hspace{0.75em} 0\\
0 & 0 & \hspace{0.75em} 1 & \hspace{0.75em} 0\\
0 & 0 & \hspace{0.75em} 0 & \hspace{0.75em} 1
\end{array} \right] \left[ \begin{array}{c}
x^0\\
x^1\\
x^2\\
x^3
\end{array} \right]
$$

ou ainda, em forma compacta,
$$
x^{\prime \mu} = \Lambda_{\nu}^{\mu} x^{\nu}, \hspace{0.75em} \mu = 0, 1, 2, 3;
$$

onde a soma sob o índice \(\nu\) está subentendida. A invariância do intervalo, \(ds^{\prime 2} = ds^2\) , implica em
$$
\eta_{\mu \nu} dx^{\prime \mu} dx^{\prime \nu} = \eta_{\mu \nu}
\Lambda_{\hspace{0.3em} \alpha}^{\mu} dx^{\alpha} \Lambda_{\hspace{0.3em}
\beta}^{\nu} dx^{\beta} = \eta_{\mu \nu} dx^{\mu} dx^{\nu}
$$

e, por conseguinte, vale
$$
\eta_{\mu \nu} \Lambda_{\hspace{0.3em} \alpha}^{\mu}
\Lambda_{\hspace{0.3em} \beta}^{\nu} = \eta_{\alpha \beta} .
$$

A exigência da invariância entre separações de eventos define uma métrica \(\eta\) no espaço-tempo, a chamada métrica de Minkowsky. Tomando \(\mathbf{x}\) e \(\mathbf{y}\) como vetores de \(M_4\) definimos uma aplicação bilinear e simétrica satisfazendo

• \(\mathbf{\eta} \left( \mathbf{x}, \mathbf{x} \right) = \left|
  \mathbf{x} \right|^2\) , onde \(\left| \mathbf{x} \right|\) é a norma ou comprimento de \(\mathbf{x}\)
• \(\mathbf{\eta} \left( \mathbf{x}, \mathbf{y} \right) = \mathbf{\eta}
  \left( \mathbf{y, x} \right)\)
• \(\eta \left( \mathbf{x}, \mathbf{x} \right) \hspace{0.75em} \left\{
  \begin{array}{c}
  = 0\\
  > 0\\
  < 0
  \end{array} \right. \begin{array}{c}
  \hspace{0.75em} \text{separação tipo luz,}\\
  \hspace{0.75em} \text{separação tipo espaço,}\\
  \hspace{0.75em} \text{separação tipo tempo.}
  \end{array}\)

Observe, no entanto, que ela não é positiva como a métrica euclidiana, definida pelo produto interno ou produto escalar. Dizemos que \(M_4\) é um espaço pseudo-euclidiano.

Usando como base de \(M_4\) os vetores \(\left\{ \mathbf{\hat{e}}_{\mu} \right\} = \left\{ \hat{t}, \hat{\imath}, \hat{\jmath},
\hat{k} \right\}\) podemos obter os componentes da métrica
$$
\eta_{\mu \nu} = \mathbf{\eta} \left( \mathbf{\hat{e}}_{\mu} \mathbf{,
\hat{e}_{\nu}} \right) = \left\{
\begin{array}{cl}
\mathbf{\eta} \left( \mathbf{\hat{e}}_0 \mathbf{, \hat{e}_0} \right) & =
– 1\\
\mathbf{\eta} \left( \mathbf{\hat{e}}_i \mathbf{, \hat{e}}_j \right) & =
\delta_{ij}\\
\mathbf{\eta} \left( \mathbf{\hat{e}}_0 \mathbf{, \hat{e}}_i \right) & =
0.
\end{array} \right. .
$$

São estes os componentes já exibidos na equação (5).

Observe que dois eventos ligados por um feixe de luz, como a emissão e captação de um fóton, por exemplo, estão separados por uma distância nula, ou seja, um vetor não nulo pode ter comprimento zero. Para ver isto fazemos
$$
ds^2 = – c^2 dt^2 + dx^2 + dy^2 + dz^2 =
$$

$$
= dt^2 \left[ – c^2 + \frac{dx^2}{dt^2} + \frac{dy^2}{dt^2} +
\frac{dz^2}{dt^2} \right] = dt^2 \left[ – c^2 + v^2 \right] = 0
$$

já que para o fóton \(v = c. \hspace{0.75em}\) Observe ainda que um vetor pode ter norma negativa ou, ainda, um vetor não nulo pode ter norma nula.
Este é o caso de vetores sobre o cone de luz
$$
– c^2 t^2 + x^2 + y^2 + z^2 = 0,
$$

O passado é composto por pontos onde ocorreram eventos que podem influenciar o evento em \(O\) por meio de alguma interação causal. Por outro lado \(O\) pode influenciar todos os eventos dentro do cone do futuro. Nenhum evento fora do cone pode afetar \(O\) nem ser por ele afetado pois não podem estar conectados por nenhuma interação com velocidade menor ou igual à da luz. A velocidade da luz é uma velocidade limite para a transmissão de qualquer informação dentro do panorama de Relatividade Especial.

Vetores e tensores de M₄

O espaço-tempo é um espaço vetorial de quatro dimensões onde a métrica ou produto interno foi definido de modo a manter invariante a separação entre eventos. Se \(\mathbf{x} \in M_4\) então \(\mathbf{x =} x^{\mu} \mathbf{\hat{e}}_{\mu}\). Usaremos a notação⁽⁸⁾
$$
\mathbf{x =} \left( x^0, x^1, x^2, x^3 \right) \text{ ou, abreviadamente, } \mathbf{x =} \left\{ x^{\mu} \right\} .
$$

Observe que \(\mathbf{x}\) é um objeto geométrico que nada tem a ver com o sistema de coordenadas escolhido enquanto enquanto os componentes \(x^{\mu}\) dependem da escolha da base \(\left\{ \mathbf{\hat{e}}_{\mu} \right\}\) e, portanto, do sistema de coordenadas utilzado. De acordo com a definição da norma temos
$$
\left| \mathbf{x} \right|^2 = \mathbf{\eta} \left( \mathbf{x}, \mathbf{x}
\right) = \mathbf{\eta} \left( x^{\mu} \mathbf{\hat{e}}_{\mu}, x^{\nu}
\mathbf{\hat{e}}_{\nu} \right) = x^{\mu} x^{\nu} \mathbf{\eta} \left(
\mathbf{\hat{e}}_{\mu}, \mathbf{\hat{e}}_{\nu} \right) = x^{\mu} x^{\nu}
\eta_{\mu \nu}
$$

e, portanto, \(\mathbf{x}\) tem comprimento invariante sob transformações de Lorentz. Diremos que \(x^{\mu}\) são os componentes contravariantes do vetor enquanto
$$
x_{\mu} = \eta_{\mu \nu} x^{\nu}
$$

são os componentes covariantes. Observe que \(x_0 = \eta_{0 \nu} x^{\nu} = – x^0\) e que, com esta notação,
$$
\left| \mathbf{x} \right|^2 = x^{\mu} x_{\mu} = – \left( x^0 \right)^2 +
x^i x_i = – \left( x^0 \right)^2 + \vec{x} \cdot \vec{x} .
$$

Se definirmos como \(\eta^{\mu \nu}\) como os componentes da matriz inversa de \(\mathbf{\eta,}\) de forma que
$$
\mathbf{\eta}^{- 1} \mathbf{\eta = I} \Rightarrow \eta^{\mu \alpha}
\eta_{\alpha \nu} = \delta_{\nu}^{\mu}
$$

então podemos retornar aos componentes contravariantes fazendo
$$
x^{\mu} = \eta^{\mu \nu} x_{\nu} .
$$

Definiremos como vetores de \(M_4\) todas as quantidades que se transformam da mesma forma que \(\mathbf{x.}\) O comprimento de todos os vetores, assim como o produto interno de dois vetores
$$
\mathbf{\eta} \left( \mathbf{u}, \mathbf{v} \right) = \mathbf{\eta} \left(
u^{\mu} \mathbf{\hat{e}}_{\mu}, v^{\nu} \mathbf{\hat{e}}_{\nu} \right) =
u^{\mu} v^{\nu} \mathbf{\eta} \left( \mathbf{\hat{e}}_{\mu},
\mathbf{\hat{e}}_{\nu} \right) = u^{\mu} v^{\nu} \eta_{\mu \nu} = u^{\mu}
v_{\mu},
$$

denominado a contração de \(\mathbf{u}\) e\(\mathbf{v,}\) são escalares, independentes do sistema de referência. Em particular será útil definir os vetores velocidade e momento, o que faremos a seguir.

Uma trajetória em \(M_4\) é uma curva parametrizada também chamada de linha mundo da partícula,
$$
P \left( \tau \right) = \mathbf{x} \left( \tau \right) = x^{\mu} \left(
\tau \right) \mathbf{\hat{e}}_{\mu},
$$

onde \(\tau\) é um parâmetro qualquer embora, com frequência, seja conveniente usar o tempo próprio. Como \(\mathbf{x}\) é um vetor de \(M_4\) então
$$
\mathbf{u =} \frac{d \mathbf{x}}{d \tau} = \frac{dx^{\mu}}{d \tau}
\mathbf{\hat{e}}_{\mu} = u^{\mu} \mathbf{\hat{e}}_{\mu}
$$

onde definimos
$$
u^{\mu} = \frac{dx^{\mu}}{d \tau} .
$$

\(\mathbf{u,}\) a quadri-velocidade, é também um vetor, tangente à linha mundo. Seus componentes são
$$
u^0 = \frac{dx^0}{d \tau} = \frac{cdt}{d \tau} = \frac{c}{\sqrt{1 –
\beta^2}},
$$

$$
u^i = \frac{dx^i}{d \tau} = \frac{dt}{d \tau} \frac{dx^i}{dt} =
\frac{v^i}{\sqrt{1 – \beta^2}} .
$$

Portanto
$$
\mathbf{u} = \left( \frac{c}{\sqrt{1 – \beta^2}}, \frac{v_x}{\sqrt{1 –
\beta^2}}, \frac{v_y}{\sqrt{1 – \beta^2}}, \frac{v_z}{\sqrt{1 – \beta^2}}
\right) = \gamma \left( c, \hspace{0.75em} \vec{v} \right) .
$$

A partir desta velocidade construimos outro vetor paralelo à 4-velocidade, o 4-momento
$$
\mathbf{p =} m \mathbf{u} = mu^{\mu} \mathbf{\hat{e}}_{\mu},
$$

onde \(m\) é a massa da partícula. Seus componentes são
$$
\mathbf{p} = \left( \frac{mc}{\sqrt{1 – \beta^2}}, \frac{m \vec{v}}{\sqrt{1
– \beta^2}} \right) = m \gamma \left( c, \sim \vec{v} \right) .
$$

No referencial comóvel \(\vec{v} = 0\) e \(\gamma = 1\) e, portanto, estes vetores assumem as formas particulares
$$
u^{\mu} = \left( c, \vec{0} \right) \hspace{1.5em} \text{ e } \hspace{1.5em} p^{\mu} = \left( mc, \vec{0}
\right) .
$$

Como se verá \(\mathbf{p}\) é uma constante do movimento enquanto o momento linear tridimensional \(\vec{p} = m \vec{v} \mathbf{,}\) que é uma quantidade conservada classicamente, não se conserva na TRE. As normas de \(\mathbf{u}\) e\(\mathbf{p,}\) em qualquer referencial inercial, são
$$
\left| \mathbf{u} \right|^2 \mathbf{=} u^{\mu} u_{\mu} = – \left( u^0
\right)^2 + u^i u_i = \gamma^2 \left( – c^2 + v^2 \right) = \frac{- c^2 +
v^2}{1 – \beta^2} = – c^2 ;
$$

$$
\left| \mathbf{p} \right|^2 = p^{\mu} p_{\mu} = m^2 u^{\mu} u_{\mu} = – m^2
c^2 .
$$

Tensores do espaço-tempo O mais simples dos tensores é um escalar, um tensor de ordem zero. Escalares são invariantes sob transformações de Lorentz, como ocorre com a separação de eventos \(ds^2\) , com o tempo próprio \(\tau\) , ou com a norma do vetor quadrivelocidade, \(\left| \mathbf{u} \right|^2 = – c^2\).

Um vetor é um tensor de ordem um, um objeto de quatro componentes que se transforme como \(x^{\mu}\) :
$$
A^{\prime \mu} = \Lambda_{\nu}^{\mu} A^{\nu} .
$$

O vetor quadri-velocidade e o quadri-momento são exemplos. Um tensor mais geral, de ordem \(r\) é um objeto com \(4^r\) componentes que se transforma deacordo com
$$
A^{\prime \alpha \beta \ldots \gamma} = \Lambda_{\mu}^{\alpha}
\Lambda_{\nu}^{\beta} \ldots \Lambda_{\rho}^{\gamma} A^{\mu \nu \ldots
\rho} .
$$

Um exemplo é o tensor formada pelo produto externo \(x^{\mu} x^{\nu}\).

Dinâmica Relativística

A teoria da relatividade afirma que observadores em movimento relativo concordam quanto à forma das equações que descrevem os fenômenos observados. é necessário então descobrir a lei de transformação que leva à descrição feita em um referencial para o outro. Matematicamente esta é uma transformação particular de coordenadas, que passamos a explorar.

Suponhamos que dois observadores em movimento relativo analisam um pulso de luz. Cada observador está em repouso nos referenciais \(S\) e \(S^{\prime}\) com origens respectivamente em \(O\) e \(O^{\prime} . \hspace{0.75em} S^{\prime}\) se move com velocidade \(v\) no direção do eixo \(Ox\) em relação a \(S\). Como a velocidade da luz é a mesma em todos os referenciais inerciais, o que foi demonstrado pelo experimento de Michelson-Morley, os observadores devem ver o pulso de luz se afastando de forma esférica. Se isto não fosse verdade um dos observadores seria capaz de determinar seu movimento relativo em relação ao outro, o que contradiz o princípio da relatividade. Consideremos ainda dois eventos infinitesimalmente próximos ligados por este raio de luz. Para os observadores em \(S\) e \(S^{\prime}\) estes eventos estarão separados por \(ds^{\prime}\) e \(ds^{\prime,}\) respectivamente dados por
$$
ds^2 = – dt^2 + dx^2 + dy^2 + dz^2,
$$

$$
ds^{\prime 2} = – dt^{\prime 2} + dx^{\prime 2} + dy^{\prime 2} +
dz^{\prime 2} .
$$

Devido à invariância da velocidade da luz estas separação deverão ser iguais, \(ds^{\prime 2} = ds^2\). Observamos que a transformação de Galileu não deixa invariante uma frente de onda de luz que satisfaz, no referencial em repouso com relação à fonte, a equação \(x^2 + y^2 + z^2 = c^2 t^2\). Sabemos da observação⁽⁵⁾ que partículas livres seguem trajetórias que são linhas retas e isto deve ser preservado em qualquer referencial inercial. Procuramos então uma transformação linear⁽⁶⁾ na forma de
$$
\begin{array}{cl}
x^{\prime} & = \alpha x + \mu t\\
y^{\prime} & = y\\
z^{\prime} & = z\\
t^{\prime} & = \lambda x + \delta t,
\end{array}
$$

onde \(\alpha, \hspace{0.75em} \beta, \hspace{0.75em} \gamma \hspace{0.75em} \text{e} \hspace{0.75em} \delta \hspace{0.75em} \) são constantes a determinar. Sem perda de generalidade podemos colocar o observador fixo na origem de \(S^{\prime}\) e, portanto, sua coordenada \(x^{\prime} = 0\) enquanto \(x\) será sua coordenada do ponto de vista do observador em \(S\). Como consequência
$$
x^{\prime} = \alpha x + \mu t = 0 \Rightarrow \frac{x}{t} = v = –
\frac{\mu}{\alpha} .
$$

Já um observador fixo na origem de \(S\) \(\left( x = 0 \right)\) terá em \( S^{\prime} \) as coordenadas
$$
x^{\prime} = – \alpha vt ; \hspace{0.75em} t^{\prime} = \delta t.
$$

O referencial \(S\) se afasta de \(S^{\prime}\) com velocidade \(– v\) e
$$
\frac{x^{\prime}}{t^{\prime}} = – v = – \frac{\alpha}{\delta} v
$$

e, portanto \(\alpha = \delta\). Resta descobrir \(\alpha\) e \(\gamma\) na transformação
$$
\begin{array}{cl}
x^{\prime} & = \alpha \left( x – vt \right)\\
t^{\prime} & = \lambda x + \alpha t.
\end{array}
$$

Para o observador em \(S^{\prime}\) a frente de onda será vista como
$$
x^{\prime 2} + y^{\prime 2} + z^{\prime 2} = c^2 t^{\prime 2} \Rightarrow
\alpha^2 \left( x – vt \right)^2 + y^2 + z^2 = c^2 \left( \lambda x +
\alpha t \right)^2 \Rightarrow
$$

$$
x^2 \left( \alpha^2 – \lambda^2 c^2 \right) + y^2 + z^2 – 2 xt \left(
\alpha^2 v + c^2 \alpha \lambda \right) = c^2 t^2 \left( \alpha^2 –
\alpha^2 v^2 / c^2 \right) .
$$

Para igualarmos esta expressão à \(x^2 + y^2 + z^2 = c^2 t^2\) devemos ter
$$
\alpha^2 – \lambda^2 c^2 = 1 ; \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \alpha^2 – \alpha^2 v^2 / c^2 ;
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \alpha^2 v
+ c^2 \alpha \lambda = 0,
$$

cuja solução é
$$
\alpha = \frac{1}{\sqrt{1 – \left( v / c \right)^2}}, \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \lambda = \frac{- v /
c^2}{\sqrt{1 – \left( v / c \right)^2}} .
$$

As transformações de coordenadas que deixam invariante a frente de onda luminosa são as chamadas transformações de Lorentz e são dadas por

$$
x^{\prime} = \frac{x – vt}{\sqrt{1 – \left( v / c \right)^2}},
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} y^{\prime} = y
$$

$$
t^{\prime} = \frac{t – vx / c^2}{\sqrt{1 – \left( v / c \right)^2}},
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em} z^{\prime} =
z. \label{TransfLorentz}
$$
As transformações inversas, para se transformar a descrição do referencial \(S^{\prime}\) para \(S\) , pode ser obtida simplesmente lembrando que \(S\) se move com velocidade \(– v\) em relação a \(S^{\prime}\). Portanto
$$
x = \frac{x^{\prime} + vt^{\prime}}{\sqrt{1 – \left( v / c \right)^2}},
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} y = y^{\prime}
$$

$$
t = \frac{t^{\prime} + vx^{\prime} / c^2}{\sqrt{1 – \left( v / c
\right)^2}}, \hspace{0.75em} \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} z = z^{\prime} .
$$

Revisando a contração espacial e dilatação temporal

Uma vez obtidas as transformações de Lorentz os efeitos da contração espacial e dilatação \ temporal se tornam mais fáceis de serem verificados. Suponha por exemplo, que queremos medir o comprimento de uma régua que tem uma ponta em \(x_1\) e a outra em \(x_2\). No referencial de repouso seu comprimento será
$$
L_0 = x_2 – x_1 .
$$

Para um observador em movimento, com velocidade \(v\) ao longo do comprimento da régua, seu comprimento será
$$
L = x_2^{\prime} \left( t^{\prime} \right) – x_1^{\prime} \left( t^{\prime}
\right) .
$$

Observe que as medidas de cada ponto devem ser feitas no mesmo instante, \(t^{\prime}\). De acordo com a transformação de Lorentz temos
$$
x^{\prime} = \gamma \left( x – vt \right) \Rightarrow x = \gamma \left(
x^{\prime} + vt^{\prime} \right)
$$

e, portanto,
$$
\begin{array}{cl}
x_2 = & \gamma \left( x_2^{\prime} + vt^{\prime} \right)\\
x_1 = & \gamma \left( x_1^{\prime} + vt^{\prime} \right)
\end{array} .
$$

Dai podemos concluir que o observador em movimento mede um comprimento \(L\) para a régua menor que o medido no referencial de repouso:
$$
L_0 = x_2 – x_1 = \gamma \left( x_2^{\prime} – x_1^{\prime} \right) =
\gamma L.
$$

Invariância da equação de onda

Um exercício interessante pode ser feito para mostrar que a equação a equação de onda para a luz é invariante sob a transformação de Lorentz. Das equações de Maxwell se pode deduzir que a luz obedece a equação
$$
\left[ \frac{\partial^2}{\partial x^2} + \frac{\partial^2}{\partial y^2} +
\frac{\partial^2}{\partial z^2} – \frac{1}{c^2} \frac{\partial^2}{\partial
t^2} \right] \Phi \left( x, y, z, t \right) = 0,
$$

que é a equação de onda se propagando com velocidade \(c\). Em um referencial em movimento \(S^{\prime}\) teremos
$$
\left[ \frac{\partial^2}{\partial x^{\prime 2}} +
\frac{\partial^2}{\partial y^{\prime 2}} + \frac{\partial^2}{\partial
z^{\prime 2}} – \frac{1}{c^2} \frac{\partial^2}{\partial t^{\prime 2}}
\right] \Phi \left( x^{\prime}, y^{\prime}, z^{\prime}, t^{\prime} \right)
= 0
$$

sendo que \(\Phi\) é um escalar, satisfazendo portanto \(\Phi \left( x, y, z, t \right) = \Phi \left( x^{\prime}, y^{\prime}, z^{\prime}, t^{\prime} \right)\). Para simplificar as operações vamos considerar o caso de uma onda plana, com propagação na direção de \(x\) apenas, descrita por \(\Phi \left(x, t \right)\). Para relacionar as derivadas temos
$$
x^{\prime} = \gamma \left( x – vt \right) ; \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} t^{\prime} = \gamma \left( t – vx / c^2
\right),
$$

e, portanto, as derivadas espaciais e temporal em termos das novas
variáveis:
$$
\frac{\partial \Phi}{\partial x} = \frac{\partial \Phi}{\partial
x^{\prime}} \frac{\partial x^{\prime}}{\partial x} + \frac{\partial
\Phi}{\partial t^{\prime}} \frac{\partial t^{\prime}}{\partial x} = \gamma
\frac{\partial \Phi}{\partial x^{\prime}} – \frac{\gamma v}{c^2}
\frac{\partial \Phi}{\partial t^{\prime}},
$$

$$
\frac{\partial \Phi}{\partial t} = \frac{\partial \Phi}{\partial
x^{\prime}} \frac{\partial x^{\prime}}{\partial t} + \frac{\partial
\Phi}{\partial t^{\prime}} \frac{\partial t^{\prime}}{\partial t} = –
\gamma v \frac{\partial \Phi}{\partial x^{\prime}} + \gamma \frac{\partial
\Phi}{\partial t^{\prime}} .
$$

Os operadores derivadas se relacionam, nos dois sistemas de coordenadas, da seguinte forma:
$$
\frac{\partial}{\partial x} = \gamma \frac{\partial}{\partial x^{\prime}} –
\frac{\gamma v}{c^2} \frac{\partial}{\partial t^{\prime}} ;
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \frac{\partial}{\partial t}
= – \gamma v \frac{\partial}{\partial x^{\prime}} + \gamma
\frac{\partial}{\partial t^{\prime}} .
$$

Podemos construir a regra de transformação para as derivadas segundas,
$$
\frac{\partial^2}{\partial x^2} = \frac{\partial}{\partial x} \left(
\frac{\partial}{\partial x} \right) = \left( \gamma
\frac{\partial}{\partial x^{\prime}} – \gamma \frac{v}{c^2}
\frac{\partial}{\partial t^{\prime}} \right) \left( \gamma
\frac{\partial}{\partial x^{\prime}} – \gamma \frac{v}{c^2}
\frac{\partial}{\partial t^{\prime}} \right) =
$$

$$
= \gamma^2 \left( \frac{\partial^2}{\partial x^{\prime 2}} – \frac{2
v}{c^2} \frac{\partial^2}{\partial x^{\prime} \partial t^{\prime}} +
\frac{v^2}{c^4} \frac{\partial^2}{\partial t^{\prime 2}} \right) ;
$$

$$
\frac{\partial^2}{\partial t^2} = \frac{\partial}{\partial t} \left(
\frac{\partial}{\partial t} \right) = \left( – \gamma v
\frac{\partial}{\partial x^{\prime}} + \gamma \frac{\partial}{\partial
t^{\prime}} \right) \left( – \gamma v \frac{\partial}{\partial x^{\prime}}
+ \gamma \frac{\partial}{\partial t^{\prime}} \right) =
$$

$$
= \gamma^2 \left( v^2 \frac{\partial^2}{\partial x^{\prime 2}} – 2 v
\frac{\partial^2}{\partial x^{\prime} \partial t^{\prime}} +
\frac{\partial^2}{\partial t^{\prime 2}} \right) .
$$

Escrevendo a equação de onda no referencial em movimento temos
$$
\left[ \frac{\partial^2}{\partial x^2} – \frac{1}{c^2}
\frac{\partial^2}{\partial t^2} \right] \Phi = 0 \Rightarrow
$$

$$
\gamma^2 \left[ \frac{\partial^2 \Phi}{\partial x^{\prime 2}} \left( 1 –
\frac{v^2}{c^2} \right) – \frac{1}{c^2} \frac{\partial^2 \Phi}{\partial
t^{\prime 2}} \left( 1 – \frac{v^2}{c^2} \right) \right] = 0,
$$

ou, simplesmente,
$$
\frac{\partial^2 \Phi}{\partial x^{\prime 2}} – \frac{1}{c^2}
\frac{\partial^2 \Phi}{\partial t^{\prime 2}} = 0,
$$

o que mostra a invariância da equação de onda sob transformações de Lorentz. De fato se pode mostrar que as equações de Maxwell são invariantes sob estas transformações. Lorentz deduziu corretamente a formas destas transformações à partir das equações do eletromagnetismo, mas não foi capaz de aplicá-las ao uso da mecânica, como fez Einstein.

Transformação de velocidades

A partir das transformações de Lorentz
$$
x^{\prime} = \gamma \left( x – vt \right), \hspace{0.75em} \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} y^{\prime} = y, \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} z^{\prime} = z,
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em} t^{\prime}
= \gamma \left( t – vx / c^2 \right),
$$

podemos obter uma expressão para a relação entre velocidades nos dois referenciais inerciais. Denotamos por
$$
u_x = dx / dt \text{e} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em}
u_x^{\prime} = dx^{\prime} / dt^{\prime}
$$

as velocidades em \(S\) e \(S^{\prime}\) respectivamente e calculamos as diferenciais
$$
dx^{\prime} = \gamma \left( dx – vdt \right), \hspace{0.75em}
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} dy^{\prime} = dy,
\hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em} dz^{\prime}
= dz, \hspace{0.75em} \hspace{0.75em} \hspace{0.75em} \hspace{0.75em}
dt^{\prime} = \gamma \left( dt – v / c^2 dx \right) .
$$

O componente em \(x\) da velocidade é
$$
u_x^{\prime} = \frac{dx^{\prime}}{dt^{\prime}} = \frac{dx – vdt}{dt – v /
c^2 dx} = \frac{u_x – v}{1 – v / c^2 u_x} .
$$

Na última igualdade dividimos numerador e denominador por \(dt\). Da mesma forma podemos encontrar o componente \(y\) ,
$$
u_y^{\prime} = \frac{dy^{\prime}}{dt^{\prime}} = \frac{dy}{\gamma \left( dt
– v / c^2 dx \right)} = \frac{u_y}{\gamma \left( 1 – v / c^2 u_x \right)},
$$

e o componente \(z\) ,
$$
u_z^{\prime} = \frac{dz^{\prime}}{dt^{\prime}} = \frac{dz}{\gamma \left( dt
– v / c^2 dx \right)} = \frac{u_z}{\gamma \left( 1 – v / c^2 u_x \right)} .
$$

Isto mostra que os vetores velocidades não se somam da mesma forma que na mecânica de Newton.

Exemplo: Uma partícula A se move com velocidade \(v_A = 0, 5 c\) no referencial do laboratório, e emite uma partícula B com velocidade \(v_B = 0, 5 c\) em relação à sua própria velocidade. Qual a velocidade \(W\) da partícula B no laboratório? O laboratorio tem velocidade \(– v_A\) em relação a partícula:
$$
W = \frac{v_A + v_B}{1 + v_A v_B / c^2} = \frac{c}{1 + \left( 0, 5
\right)^2} = 0, 8 c.
$$

Tempo Próprio

Vimos que as medidas do tempo variam com a velocidade do observador que analisa o fenômeno sob consideração. O tempo próprio \(\tau\) de uma partícula é definido como o tempo medido por um observador que se move junto com a partícula, no chamado referencial comóvel. Neste caso \(dx = dy = dz = 0\) para o este observador. Como a separação em \(M_4\) é invariante temos, em comparação com um outro observador qualquer, temos que
$$
ds^2 = – c^2 d \tau^2 = – c^2 dt^2 + dx^2 + dy^2 + dz^2,
$$

ou seja,
$$
d \tau^2 = dt^2 – \frac{1}{c^2} \left( dx^2 – dy^2 – dz^2 \right) = \left(
1 – \frac{v^2}{c^2} \right) dt^2,
$$

onde foi feita a substituição
$$
v^2 = \left( \frac{dx}{dt} \right)^2 + \left( \frac{dy}{dt} \right)^2 +
\left( \frac{dz}{dt} \right)^2,
$$

sendo \(v\) a velocidade relativa entre os dois referenciais e, por conseguinte, a velocida da partícula estudada pelo observador não comóvel. Podemos ainda escrever
$$
d \tau = dt \sqrt{1 – \left( v / c \right)^2} = dt \sqrt{1 – \beta^2}
$$

e, como consequência
$$
\frac{dt}{d \tau} = \frac{1}{\sqrt{1 – \beta^2}} .
$$

O tempo próprio é um escalar
$$
d \tau^2 = \frac{- 1}{c^2} ds^2
$$

e portanto invariante sob mudanças de coordenadas que satisfazem as transformações de Lorentz. Por este motivo é um bom candidato a ser usado como parâmetro nas equações do movimento.

A estrutura do espaço-tempo

Como veremos, a simples exigência de que a velocidade da luz seja a mesma quando medida por um observador em um referencial inercial qualquer implica em profundas consequências tanto para o entendimento da mecânica quanto da estrutura do espaço-tempo.

Simultaneidade

Considere a situação ilustrada na figura 2. Dois eventos ocorrem em \(P\) e \(P^{\prime}\) igualmente distantes do observador \(O\) que está em repouso. Está observador poderá, por exemplo, coletar luz emitida pelos eventos e concluirá que os eventos foram simultâneos.

Outro observador \(O^{\prime}\) está em movimento na direção da separação entre os eventos. Como os sinais de luz levam algum tempo para alcançá-lo ele terá se deslocado de \(\Delta x\) na direção de \( P^{\prime}\) e, portanto, afirmará que \(P^{\prime}\) ocorreu antes que \(P\). Isto mostra que a simultaneidade não é um conceito absoluto. No entanto um observador em movimento transversal com relação à separação \(PP^{\prime}\), com qualquer velocidade, afirmará que os eventos ocorreram ao mesmo tempo.

Dilatação temporal

Na apresentação da TRE Einstein muitas vezes considerou necessário descrever uma forma operacional para se medir uma determinada quantidade. Para medir um intervalo de tempo, por exemplo, nada melhor que construir um relógio de luz, dada a constância de sua velocidade para todos os referenciais inerciais. Considere que dois observadores medem um intervalo de tempo, um deles no referencial \(O\) que se move com velocidade v em relação a \(O^{\prime}\). Um sinal de luz é emitido do ponto \(P_1\) , refletido por um espelho e coletado de volta em \(P_2\) ,como ilustrado na figura 3.

O observador \(O\) carrega consigo o relógio de luz e verifica que o tempo completo de ida e volta do sinal de luz é \(T = 2 \Delta t\) onde
$$ \Delta t = \frac{L}{c} . $$

O observador \(O^{\prime}\) , por sua vez, vê o relógio passar com velocidade \(v\) e medirá um intervalo de tempo \(T^{\prime} = 2 \Delta t^{\prime}\). Observe na figura que, pelo teorema de Pitágoras, temos
$$
L^{\prime 2} + \left( v \Delta t^{\prime} \right)^2 = \left( c \Delta
t^{\prime} \right)^2
$$

e, portanto,
$$
L^{\prime 2} = \Delta t^{\prime 2} \left( c^2 – v^2 \right) .
$$

Concluimos dai que
$$
\Delta t^{\prime} = \frac{L^{\prime}}{\sqrt{c^2 – v^2}} =
\frac{L^{\prime}}{c} \frac{1}{\sqrt{1 – \left( v / c \right)^2}} .
$$

Observe que \(L^{\prime} = L\) , pois não há ambiguidade no comprimento de distâncias perpendiculares à direção do movimento, logo
$$
T = \frac{2 L}{c}, \hspace{0.75em} T^{\prime} = \frac{2 L}{c}
\frac{1}{\sqrt{1 – \left( v / c \right)^2}} .
$$

Concluimos que
$$
T^{\prime} = \frac{T}{\sqrt{1 – \left( v / c \right)^2}},
$$
ou seja, o observador \(O^{\prime}\) mede intervalos de tempo maiores para o relógio em movimento, se comparado com as medidas do observador \(O\) , que está em repouso em relação ao relógio.

Contração espacial

Colocamos agora uma régua para medir a distância entre \(P_1\) e \(P_2\) nos dois referenciais. No primeiro caso ilustrado na figura 4, um observador \(O^{\prime}\) em repouso em relaçao à régua vê o feixe de luz ser emitido em \(P_1\) e recoletado em \(P_2\).

Como, para este observador, o intervalo de tempo gasto pela luz para percorrer o trajeto de ida é volta é \(T^{\prime}\), dado pela equação 3, a distância medida é \(R_0 =\) \(\overline{P_1 P_2} = vT^{\prime}\). Do ponto de vista do observador em \(O\) o relógio está fixo enquanto régua se move com velocidade \(– v\) e o tempo envolvido é \(T\). Portanto a distância percorrida é \( R = vT. \) Como conclusão os dois observadores medem uma distância diferente, relacionadas por
$$
\frac{R_0}{R} = \frac{T^{\prime}}{T} = \frac{1}{\sqrt{1 – \left( v / c
\right)^2}},
$$

o que representa uma contração espacial no sentido do movimento. O observador em movimento em relação à régua, vê seu comprimento como
$$
R = \sqrt{1 – \left( v / c \right)^2} R_0,
$$

onde \(R_0\) é o comprimento obtido por um observador parado em relação à régua.

é costume se definir os seguintes termos para o uso no contexto da TRE. A velocidade relativa do referencial ou objeto em estudo é
$$
\beta = \frac{v}{c},
$$

enquando

$$
\gamma = \frac{1}{\sqrt{1 – \left( \frac{v}{c} \right)^2}} =
\frac{1}{\sqrt{1 – \beta^2}} . \label{Gamma}
$$
Com estas definições podemos escrever
$$
T^{\prime} = \gamma T^{\prime}, \text{} R^{\prime} = R \sqrt{1 – \beta^2} .
$$

Concluímos que dois observadores em movimento relativo obtém diferentes resultados para medidas de intervalos de tempo e de distância ao longo do movimento. Cada observador verá as réguas do outro com menores comprimentos e seus relógios batendo mais devagar. Este fenômeno é irrelevante para os objetos da experiência diária, que têm velocidades pequenas se comparadas à da luz. No entanto dentro de aceleradores de partículas é possível acelerar partículas até velocidades muito próximas de \(c\) e, nesta situação, os efeitos relativísticos se tornam importantes.

Inúmeros exemplos podem ser citados como comprovação experimental destes resultados. Dentro dos aceladores de partículas são produzidas partículas \(\tau\) (tau), que têm meia-vida aproximada de \(3, 05 \times 10^{- 13}\) s quando observadas por um observador em repouso no referencial do laboratório. Elas se apresentam com velocidades muito altas, bem próximas da velocidade da luz⁽⁴⁾. Portanto, estas partículas não pode viajar em média uma distância superior a
$$
d = 3 \times 10^8 \hspace{0.25em} \text{m.s}^{- 1} \times 3, 05 \times
10^{- 13} \hspace{0.25em} \text{s} = 9, 15 \times 10^{- 5} \hspace{0.25em}
\text{m},
$$

antes que decaiam sob a forma de outras partículas. No entanto se observa que elas viajam por distâncias muito superiores a esta! A solução para o aparente paradoxo está na TRE. No referencial do laboratório as partículas estão em altas velocidades e por isto seus relógios internos batem mais devagar, permitindo uma viagem mais longa antes do decaimento. Para um referencial colocado sobre as partículas, o chamado referencial comóvel, o tempo flui inalterado mas as distâncias ao longo do movimento ficam contraídas e o resultado final é o mesmo.

Ambos os fenômenos dependem do fator \(\gamma\) definido acima. Partículas \(\tau\) geradas no SLAC, Stanford Linear Accelerator Collider atingem tipicamente \(\gamma = 20\) e as partículas viajam por uma distância média de
$$
20 \times (9, 15 \times 10^{- 5} \hspace{0.25em} \text{m}) = 1, 8 \times
10^{- 2} \hspace{0.25em} \text{m} \approx 1, 8 \hspace{0.25em}
\text{mm}.
$$

Na prática, em um laboratório, a medida do alcance média das partículas é usada para se calcular a meia-vida do \(\tau\).

As transformações de Lorentz