data science

NumPy, Introdução

Posted on by Guilherme


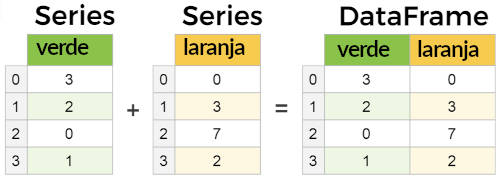
Numpy

NumPy é uma biblioteca do python especializada em computação científica e análise de dados. Ela é usada em diversos tipos de operações que envolvem operações matriciais. Além disso suas matrizes formam a base para outros pacotes, como o pandas e outras voltadas para o cálculo matemático e científico. Numpy foi primeiro lançado por Travis Oliphant em 2006 e tem sido mantido por um grande número de colabores desde então, sob licença BSD.

NumPy, com suas matrizes, apresenta algumas vantagens sobre o cálculo usual com objetos do python, como listas e tuplas. Essas operações são mais rápidas e flexíveis e foram construídas de forma a evitar a necessidade da realização de laços (loops ). Ela contém métodos voltados para operações da álgebra linear, geração de números aleatórios e transformadas de Fourier, além da interface voltada para a conexão com as linguagens C, C++ e FORTRAN.

Um exemplo rápido pode mostrar como as rotinas do numpy são mais eficientes que as de objetos list do python.

» # comparação de velocidades
» import numpy as np
» # um array do numpy
» array = np.arange(1_000_000)
» # uma lista usual do python
» lista = list(range(1_000_000))

» %time for _ in range(100): arr2 = array * 2
↳ CPU times: user 145 ms, sys: 7.93 ms, total: 152 ms
  Wall time: 151 ms

» %time for _ in range(100): lista2 = [x * 2 for x in lista]
↳ CPU times: user 5.35 s, sys: 778 ms, total: 6.13 s
  Wall time: 6.12 s

» # 5.35/.145 ≈ 37 × mais rápido

Wall time é o tempo total gasto pelo código para ser executado. CPU time é uma medida do tempo gasto pelo processador apenas quando esteve operando sobre a tarefa específica. Dependendo do cálculo feito o numpy pode ser mais de 100 vezes mais rápido que uma operação similar em puro python.

Instalação


Em geral o módulo está presente como pacote na maioria das distribuições de Python. Se necessária a sua instalação em separado pode ser feita. Numpy e pandas são instalados juntos com o Anaconda.

# No Linux (Ubuntu and Debian):
» sudo apt-get install python-numpy
# No Linux (Fedora)
» sudo yum install numpy scipy
# No Windows com Anaconda:
» conda install numpy
# após a instalação o módulo deve ser importado:
» import numpy as np
# O aliás np é opcional e de escolha do programador.

Ndarray

O objeto básico da biblioteca Numpy é o ndarray (N-dimensional array). Ndarrays são matrizes multidimensionais com número determinado de dimensões e elementos. Seus elementos pertencem todos a um único tipo, chamado de dtype (data-type ou tipo de dado). Cada dimensão é denominada por axis (eixo) e o número de eixos é o rank do objeto. Diferente das listas do python, ndarrays têm dimensões fixas, definidas em sua construção.

Um ndarray possui os seguintes atributos referentes ao seu tipo de dado, tamanho e ordem:

Atributo descrição
array.dtype tipo de dado armazenado. (Veja lista abaixo),
array.ndim número de dimensões (que são eixos ou axis ); o mesmo que rank
array.size número de elementos em cada eixo,
array.shape (ou forma), tupla de N inteiros positivos com o comprimento de cada eixo.

Um ndarray de 1 dimensão é um objeto similar a um vetor (rank = 1): arr1D = ([a0,a1,...,aN-1,]), arr1D.size = N, arr1D.ndim = 1, arr1D.shape = (N,).

Um ndarray de 2 dimensões é um objeto similar a uma matriz (rank = 2): se ela possui M linhas, cada uma com N elementos então arr2D.size = M × N , arr2D.ndim = 2, arr2D.shape = (M,N).

Um ndarray de 3 dimensões é uma coleção de matrizes (rank = 3): se ela possui K matrizes de M linhas, cada uma com N elementos então arr3D.size = K × M × N , arr3D.ndim = 3, arr3D.shape = (K, M, N).

Ndarrays de ordem superior são generalizações desse processo, acrescentados novos eixos.

Os eixos são numerados para diversas operações. Em 2 dimensões axis=0 são as linhas, axis=1 as colunas, e assim consecutivamente para ordens superiores.

Tipos, dtypes

Além dos tipos usuais do python, a importação de Numpy disponibiliza um conjunto extendido de tipos ou dtypes.

dtype descrição
bool booleano (true ou false) armazenado como um byte
intX inteiro com sinal, X-bit (X=8,16,32, 64)
uintX inteiro sem sinal, X-bit (X=8,16,32, 64)
intc idêntical ao int C (em geral int32 ou int64)
intp inteiro usado para indexação (como C size_t; em geral int32 ou int64)
float_ o mesmo que float64
float16 meia precisão float: sign bit, 5-bit exponente, 10-bit mantissa
float32 simple precisão float: sign bit, 8-bit exponente, 23-bit mantissa
float64 dupla precisão float: sign bit, 11-bit exponente, 52-bit mantissa
complex_ o mesmo que complex128
complex64 complexo, representado por dois 32-bit floats (parte real e imaginária)
complex128 complexo, representado por dois 64-bit floats (parte real e imaginária)

Construção de um array

Um array do NumPy pode ser criado passando-se uma lista para construtor np.array(lista).

» import numpy as np

» lista = [123,234,345]
» arr = np.array(lista)
» arr
↳ array([123, 234, 345])

# o objeto criado é um ndarray do numpy
» type(arr)
↳ numpy.ndarray

» arr.dtype
↳ dtype('int64')

» arr.ndim
↳ 1
» arr.shape
↳ (3,)
» arr.size
↳ 3

» # uma lista de listas
» lista2 = [[123,234,345],
            [456,567,678],
            [789,890,901]]
» arr2 = np.array(lista2)
» arr2
↳ array([[123, 234, 345],
         [456, 567, 678],
         [789, 890, 901]])

» arr2.ndim
↳ 2
» arr2.size
↳ 9
» arr2.shape
↳ (3, 3)

» # lista de listas de listas
» lista3 =[ [ [1,2],[2,3] ], [ [3,4],[4,5] ],  [ [1,2],[2,3] ], [ [3,4],[4,5] ] ]
» arr3 = np.array(lista3)
» # o resultado é: 4 matrizes de 2 x 2  elementos
» arr3
↳ array([[[1, 2],
         [2, 3]],

        [[3, 4],
         [4, 5]],

        [[1, 2],
         [2, 3]],

        [[3, 4],
         [4, 5]]])

» arr3.ndim
↳ 3
» arr3.shape
↳ (4, 2, 2)
» arr3.size
↳ 16

» # a 1ª matriz
» arr3[0]

↳  array([[1, 2],
         [2, 3]])

» # a 2ª linha da 1ª matriz
» arr3[0,1]
↳ array([2, 3])

» # o 1º elemento da 2ª linha da 1ª matriz
» arr3[0,1,0]
↳ 2

# todos os arrays criados tem o mesmo dtype
» arr3.dtype
↳ dtype('int64')

Arrays podem ser de outros tipos, como um array de strings. No entanto devem ser homogêneos (todos os elementos do mesmo tipo). Uma tentativa de criar um array como em stArr2 causa uma tentativa de ajuste (cast), transformando os inteiros em string. O método array(listas, dtype) aceita o parâmetro dtype onde se pode informar o tipo de elemento que se pretende armazenar.

» stArr = np.array([['a', 'b'],['c', 'd']])
» stArr
↳ array([['a', 'b'],
       ['c', 'd']], dtype='<U1')

» stArr[0,1]
↳ 'b'
» stArr.dtype
↳ dtype('<U1')
» stArr.dtype.name
↳ 'str32'

» stArr2 = np.array([[1.01, 2.02],['h', 'i']])
» stArr2
↳ array([['1.01', '2.02'],
        ['h', 'i']], dtype='<U21')

» stArr3 = np.array([[True, False],['h', 'i']])
» stArr3
↳ array([['True', 'False'],
        ['h', 'i']], dtype='<U5')

» # parâmetro dtype
» cplx = np.array([[1, 2, 3],[4, 5, 6]], dtype=complex)
» cplx
↳ array([[1.+0.j, 2.+0.j, 3.+0.j],
        [4.+0.j, 5.+0.j, 6.+0.j]])

Arrays podem ser transformados de um tipo para outro (quando possível). Para isso usamos array.astype(). Na transformação de floats para inteiros a parte decimal será truncada. Arrays de strings, desde que devidamente formatados, podem ser convertidos em numéricos.

» # criando um array de integers
» arr = np.array([1, 2, 3, 4, 5])
» arr.dtype
↳ dtype('int64')

» # cast para array de ponto flutuante
» floatArr = arr.astype(np.float64)
» floatArr.dtype
↳ dtype('float64')

» # floats para integers
» # criando um array de floats
» arr = np.array([1.9, -8.2, -9.6, 0.9, 2.3, 10.7])
» arr
↳ array([ 1.9, -8.2, -9.6, 0.9, 2.3, 10.7])

» # converte para inteiros (trunca parte inteira)
» arr.astype(np.int32)
↳ array([ 1, -8, -9, 0, 2, 10], dtype=int32)

» # um array de strings
» arrNumStrings = np.array(['0.0', '7.75', '-6.6', '100'], dtype=np.string_)
» arrNumStrings.astype(float)
↳ array([ 0., 7.75, -6.6 , 100.]

Métodos predefinidos de construção

O método np.arange(m,n,[p]) retorna um array de inteiros no intervalo (m, n], i.e., começando em m e terminando em n-1. Se o primeiro argumento for omitido m=0. Um terceiro argumento informa o p=passo, intervalo entre os valores da sequência. Em np.arange(m,n,p) m, n devem ser inteiros mas p pode ser um float.

O método np.linspace(m,n,p) retorna um array no intervalo (m, n), ambos os extremos incluídos, com p números igualmente espaçados.

np.random.random(n) retorna um array com n elementos aleatórios e np.random(m, n) retorna um array com shape = (m,n) e elementos aleatórios.

» # np.range(n)
» np.arange(10)
↳ array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

» # np.range(m,n)
» np.arange(5, 15)
↳ array([ 5,  6,  7,  8,  9, 10, 11, 12, 13, 14])

» # np.range(m,n,p)
» np.arange(10, 100, 10)
↳ array([10, 20, 30, 40, 50, 60, 70, 80, 90])

» np.arange(10, 20, .5)
↳ array([10. , 10.5, 11. , 11.5, 12. , 12.5, 13. , 13.5, 14. , 14.5, 15. ,
         15.5, 16. , 16.5, 17. , 17.5, 18. , 18.5, 19. , 19.5])

» # np.linspace(m,n,p)
» np.linspace(10, 20, 5)
↳ array([10. , 12.5, 15. , 17.5, 20. ])

» # a sequência pode ser decrescente
» np.linspace(20, 10, 5)
↳ array([20. , 17.5, 15. , 12.5, 10. ])

» # np.random.random(n)
» np.random.random(10)
↳ array([0.35433322, 0.54555179, 0.48783323, 0.5785414 , 0.76837232,
         0.69888297, 0.62492788, 0.33289321, 0.75068313, 0.95667854])

» # np.random.random(m,n)
» np.random.random((2,3))
↳ array([[0.11351481, 0.76831577, 0.27597676],
         [0.73130126, 0.7225559 , 0.54040225]])

Os métodos np.zeros((m,n)) e np.ones((m,n)) criam, respectivamente, ndarrays de zeros e uns com as dimensões dadas pela tupla (ou lista) no argumento. np.eye(m,n) gera um ndarray m × n com elementos 1 na diagonal, 0 fora dela. np.eye(n,n) é o mesmo que np.eye(n) ou np.identity(n), que são a matriz identidade de n dimensões.

» np.zeros((2,4))
↳ array([[0., 0., 0., 0.],
         [0., 0., 0., 0.]])

» np.ones((2,3))
↳ array([[1., 1., 1.],
         [1., 1., 1.]])

» np.eye(2,4)
↳ array([[1., 0., 0., 0.],
         [0., 1., 0., 0.]])

» np.identity(3)
↳ array([[1., 0., 0.],
         [0., 1., 0.],
         [0., 0., 1.]])

» np.eye(2,6)
↳ array([[1., 0., 0., 0., 0., 0.],
         [0., 1., 0., 0., 0., 0.]])

» np.eye(4,4)
↳ array([[1., 0., 0., 0.],
         [0., 1., 0., 0.],
         [0., 0., 1., 0.],
         [0., 0., 0., 1.]])

O método np.empty(m,n) permite a criação de arrays vazios, em geral destinados a serem preenchidos depois de sua criação por meio de algum cálculo ou leitura de dados. Nos exemplos criamos um array numérico vazio, arrN. Observe que não há garantia de que as entradas serão nulas. Em seguida criamos um array vazio de strings, com espaço para 3 caracteres (dtype='<U3′), e o preenchemos em um loop.

» # array numérico "vazio"
» arrN = np.empty((1,3))
» arrN
↳ array([[4.66896202e-310, 0.00000000e+000, 1.58101007e-322]])    

» # array de strings
» arr = np.empty((3,3), dtype='<U3')
» arr
↳ array([['', '', ''],
         ['', '', ''],
         ['', '', '']], dtype='<U3')

» for linha in range(arr.shape[0]):
»     for coluna in range(arr.shape[1]):
»         arr[linha,coluna] = 'a' + str(linha) + str(coluna)
» arr
↳ array([['a00', 'a01', 'a02'],
         ['a10', 'a11', 'a12'],
         ['a20', 'a21', 'a22']], dtype='<U3')

Alterando dimensões

Dado um array de uma única linha com r elementos podemos tranformá-lo em um array com shape = (m,n), desde que as dimensões sejam compatíveis, i.e., r = m × n. De fato, qualquer array pode ser transformado em outro se eles possuem o mesmo número de elementos (mesmo size ).

» arr = np.random.random(12)
» arr
↳ array([0.04276829, 0.76468762, 0.24807651, 0.75531679, 0.60327475,
         0.81704922, 0.08233836, 0.64112484, 0.55276595, 0.30669723,
         0.43989324, 0.60031761])

» # reshape
» arr.reshape(3,4)
↳ array([[0.04276829, 0.76468762, 0.24807651, 0.75531679],
         [0.60327475, 0.81704922, 0.08233836, 0.64112484],
         [0.55276595, 0.30669723, 0.43989324, 0.60031761]])

» np.linspace(0,10, 6).reshape(2,3)
↳ array([[ 0.,  2.,  4.],
         [ 6.,  8., 10.]])

Indexação e fatiamento


Quando um array é criado ele recebe automaticamente um conjunto de índices. Um elemento pode ser lido ou alterado por meio de seu índice. Índices negativos contam de trás para frente, sendo arr[-1] o último elemento do array. Para selecionar (ou editar) vários elementos passamos uma lista de índices.

» arr = np.linspace(1,12, 12)
» arr
↳ array([ 1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10., 11., 12.])

» # o 5º elemento
» arr[4]
↳ 5.

» # alterando o 5º elemento
» arr[4] = 100
» arr
↳ array([ 1.,  2.,  3.,  4.,  100.,  6.,  7.,  8.,  9., 10., 11., 12.])

» arr[-8]
↳ 100

» # lendo vários elementos
» arr[[0,2,5]]
↳ array([1., 3., 6.])

» # alterando vários elementos
» arr[[0,2,5]] = [10, 20, 30]
» arr
↳ array([ 10.,   2.,  20.,   4., 100.,  30.,   7.,   8.,   9.,  10.,  11.,  12.])

No caso de arrays bidimensionais os elementos do array são acessados pelos índices de suas linhas e colunas, sendo que arr[l,c] = al,c é o elemento da linha l e coluna c. Em objetos de ranks superiores cada índice se refere a um dos eixos.

Uma fatia ou slice do array é um subconjunto de elementos que pode ter o mesmo shape ou não. Para um vetor, digamos arr1D = [a0, a1, ..., aM] a fatia arr1D[m,n] = [am, ..., an-1], onde m ≥ 0, n ≤ M. Vale lembrar que o comprimento da fatia de um array unidimensional é arr1D[m,n].size = n-m.

» # outro teste para slices
» arr = np.arange(10)    # cria o array array([0, 1, 2, 3, 4, 5, 6, 7, 8, 9])

» arr[6:9]
↳ array([6, 7, 8])

» arr[:3]
↳ array([0, 1, 2])

» arr[7:]
↳ array([7, 8, 9])

» # uma seção pode ser alterada†
» arr[3:6] = -5
» arr
↳ array([ 0,  1,  2, -5, -5, -5,  6,  7,  8,  9])

» arr[7:] = -arr[7:]
» arr
↳ array([ 0,  1,  2, -5, -5, -5,  6, -7, -8, -9])

(†) Uma operação entre arrays de dimensões diferentes, como ocorre em arr[0:4] = -1 é chamado de propagação ou broadcasting. Para interagir com a 1ª parte da expressão a 2ª é transformada: -1 → arr[-1,-1,-1,-1]. Voltaremos a esse tópico.

Observe que uma fatia de um array é uma referência àquela parte do array e qualquer alteração feita na fatia se refletirá no array original. A notação arr[i:j] significa, claro, elementos de i-ésimo até (j-1)-ésimo. arr[:] significa todos os elementos do array.

» # criando um array de teste
» arr = (np.random.random(10)*10).round(1)
» arr
↳ array([3. , 1.5, 5.3, 1.3, 8.8, 9.8, 4.7, 0.1, 0.1, 0.6])
» fatia = arr[1:5]
» fatia
↳ array([1.5, 5.3, 1.3, 8.8])

# vamos alterar trecho da fatia
» fatia[1:3] = 0
» fatia
↳ array([1.5, 0. , 0. , 8.8])

» # o array original foi alterado
» arr
↳ array([3. , 1.5, 0. , 0. , 8.8, 9.8, 4.7, 0.1, 0.1, 0.6])

» # vamos alterar a fatia inteira
» fatia[:] = -10
» arr
↳ array([  3. , -10. , -10. , -10. , -10. ,   9.8,   4.7,   0.1,   0.1,  0.6])

» # valores específicos podem ser fornecidos (sem broadcast)
» fatia[:] = [-1,-2,-3,-4]
» arr
↳ array([ 3. , -1. , -2. , -3. , -4. ,  9.8,  4.7,  0.1,  0.1,  0.6])

Esse comportamento é útil quando se trabalha com array de dados muito grande e se deseja alterar apenas parte dele, lembrando que a biblioteca efetua suas operações mantendo os dados envolvidos na memória.

Em um array arr de 2 dimensões arr[m] é a m-ésima linha e arr[m,n] se refere ao elemento am,n, da m-ésima linha, n-ésima coluna. arr[m][n] é o mesmo am,n.

» # slices para dimensões mais altas
» arr = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]])
» arr
↳ array([[1, 2, 3],
         [4, 5, 6],
         [7, 8, 9]])

» # 2ª linha
» arr[1]
↳ array([4, 5, 6])

» arr[:1]
↳ array([[1, 2, 3]])

» # 1ª linha, 3º elemento
» arr[0,2]
↳ 3
» arr[0][2]
↳ 3

Uma cópia de um setor é uma referência para aquele setor, chamda de view ou visualização do segmento. Alterações feitas à view se refletam no array original, a menos que o método arr.copy() seja usado. Um array copiado dessa forma perde a referência com o array original e pode ser modificado independentemente.

» # slices em 3D:
» # criamos um array com shape (2,3,2)
» arr3D = np.arange(12).reshape(2,3,2)
» arr3D
↳ array([[[ 0,  1],
         [ 2,  3],
         [ 4,  5]],

        [[ 6,  7],
         [ 8,  9],
         [10, 11]]])

» # a 1ª matriz é
» arr3D[0]
↳ array([[0, 1],
        [2, 3],
        [4, 5]])
» # a 2ª linha da 1ª matriz é
» arr3D[0,1]
↳ array([2, 3])

» # seu 2º elemento
» arr3D[0,1,1] # o mesmo que arr3D[0,1][1]
↳ 1

» # copiamos um slice de 2 formas
» guardar = arr3D[0].copy()
» slice = arr3D[0]
» # ambos com os valores da  1ª matriz

» # alteramos toda a 1ª matriz
» arr3D[0] = 12
» # o array original foi alterado
» arr3D
↳ array([[[12, 12],
         [12, 12],
         [12, 12]],

        [[ 6,  7],
         [ 8,  9],
         [10, 11]]])
» # a cópia por referência foi alterada
» slice
↳ array([[12, 12],
         [12, 12],
         [12, 12]])

» # mas a cópia por valor não foi alterada
» guardar
↳ array([[0, 1],
         [2, 3],
         [4, 5]])

» # podemos restaurar o array aos seus valores originais
» arr3D[0] = guardar
» arr3D
↳ array([[[ 0,  1],
          [ 2,  3],
          [ 4,  5]],

         [[ 6,  7],
          [ 8,  9],
          [10, 11]]])


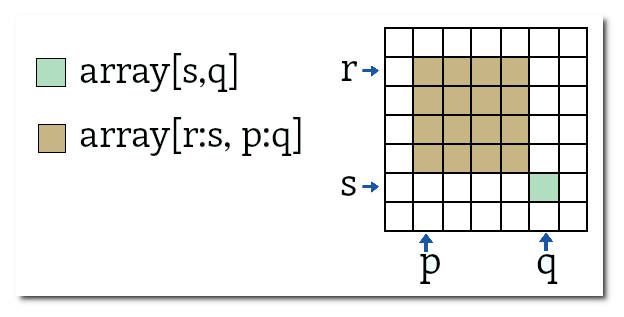
A notação de slice, idêntica à usada em listas do python, funciona em arrays. Para um array unidimensional arr1d[i:f] retorna do i-ésimo elemento até j-ésimo elemento (exclusive). Para um array de 2 dimensões arr2d[i:f] retorna i-ésima linha até j-ésima linha (exclusive). Se i é omitido o início é usado, se j é omitido o final é usado. Portanto arr2d[:2] significa as duas primeiras linhas do array (linha 0 e linha 1).

Slices ou segmentos múltiplos podem ser usados. Por exemplo, arr2d[m:n, r:s] são as linhas de m até n-1, colunas de r até s-1.

» # array 1d  (um vetor)  
» arr = np.array([1.2, 2.3, 3.4, 4.5, 5.6])
» arr[2:4]
↳ array([3.4, 4.5])

» # array 2d  (uma matriz)  
» arr2d = np.array([[1,2,3],[4,5,6],[7,8,9]])
» arr2d
↳ array([[1, 2, 3],
         [4, 5, 6],
         [7, 8, 9]])

» arr2d[0:2]
↳ array([[1, 2, 3],
         [4, 5, 6]])

» arr2d[:2]
↳ array([[1, 2, 3],
         [4, 5, 6]])
       
» # slices múltiplos
» arr2d[:2, 1:]
↳ array([[2, 3],
         [5, 6]])

arr2d[:2, 1:] são as linhas 0 e 1, colunas de 1 em diante.

O indexador pode ser um array booleano, e os valores serão filtrados apenas se o índice for True. Essa operação pode ser muito útil para a implementação de filtragens de tipos diversos.

» # o indexador pode ser booleano
» ar1 = np.array([-1,0, 3, 7, -2, 10])
» ar2 = np.array([-2,10, 2, 9, -1, 8])

» # extrair apenas 0º e 2º elemento
» ar1[[True, False, True, False, False, False]]
↳ array([-1,  3])

» # elementos de ar1 maiores que 2
» ar1[ar1>2]
↳ array([ 3,  7, 10])

» # elementos de ar1 maiores que os de ar2
» ar1[ar1>ar2]
↳ array([-1,  3, 10])

Suponha que temos dados sobre alguns países, armazenados em forma tabular. O primeiro array contém os nomes dos países, como se fosse um cabeçalho da tabela seguinte. O segundo array contém dados numéricos de qualquer natureza, com 5 linhas e 4 colunas, cada coluna contendo dados relativos ao país no cabeçalho. Para esse exemplo geramos esses dados aleatoriamente, apenas para exibir a operação.

» arrPais = np.array(['Brasil', 'Chile', 'Brasil', 'Peru'])
» arrDados = np.random.randn(5,4).round(2)  # 5 linhas e 4 colunas

» print(arrPais, '\n', arrDados)
↳ ['Brasil' 'Chile' 'Brasil' 'Peru'] 
   [[-0.71  0.42 -0.52  0.63]
   [-1.12 -0.29  0.03  1.43]
   [ 0.99  0.45  1.08  0.53]
   [-0.78  0.18 -0.07  0.28]
   [-2.03  0.44  0.07  1.28]]

» # podemos exibir todas as linhas das colunas 0 e 2
» arrDados[:,[0,2]]
↳ array([[-0.71, -0.52],
         [-1.12,  0.03],
         [ 0.99,  1.08],
         [-0.78, -0.07],
         [-2.03,  0.07]])

» # alternativamente, as colunas que correspondem ao Brasil
» arrBrasil = arrDados[:, arrPais=='Brasil']
» arrBrasil
↳ array([[-0.71, -0.52],
         [-1.12,  0.03],
         [ 0.99,  1.08],
         [-0.78, -0.07],
         [-2.03,  0.07]])

» # na tabela do Brasil, suponha que valores negativos sejam insignificantes
» # podemos eliminá-los com uma filtragem
» arrBrasil[arrBrasil < 0] = 0
» arrBrasil
↳ array([[0.  , 0.  ],
         [0.  , 0.03],
         [0.99, 1.08],
         [0.  , 0.  ],
         [0.  , 0.07]])

» # a soma desses dados é
» arrBrasil.sum()
↳ 2.17

» # para exibir os demais dados (não do Brasil)
» arrDados[:, arrPais!='Brasil'] # ou arrDados[:, ~(arrPais=='Brasil')]
↳ array([[ 0.42,  0.63],
         [-0.29,  1.43],
         [ 0.45,  0.53],
         [ 0.18,  0.28],
         [ 0.44,  1.28]])

Observe que arrPais!='Brasil' é a negação de arrPais=='Brasil'. O parênteses em ~(arrPais=='Brasil') é necessário pois a negação ~ tem precedência sobre o teste de igualdade. Sem o parênteses ~arrPais seria avaliado primeiro, o que resultaria em erro pois o array não é booleano.

As ferramentas do pandas facilitam operações como essas.

Operações matemáticas

Operações são realizadas elemento a elemento (que abreviaremos para “e/e” nesse texto). Operações usuais de um array por um escalar são são propagadas entre o escalar e cada elemento do array. Operações entre arrays são feitas e/e, ou seja, realizadas entre elementos na mesma posição. Os arrays devem ter as mesmas dimensões.

Operações de incremento, tais como array += 1 (que significa array = array + 1) ou array *= 2 são realizados inplace (alteram o próprio array). Diversas outras operações do NumPy (e do pandas) são realizadas inplace enquanto em várias delas existe o parâmetro inplace = True/False que permite a decisão de qual caso se deseja naquele momento.

Operações podem ser feitas entre arrays retornados por funções (que retornam arrays).

» # operações com escalares    
» ar1 =  np.linspace(10, 20, 5)
» ar1
↳ [10.  12.5 15.  17.5 20. ]

» ar1 + 10
↳ [20.  22.5 25.  27.5 30. ]

» ar1 * 10
↳ [100. 125. 150. 175. 200.]

» ar1 / 10
↳ [1.   1.25 1.5  1.75 2.  ]

» ar1**2
↳ [100.   156.25 225.   306.25 400.  ]

» 1/arr1
↳ array([0.1       , 0.08      , 0.06666667, 0.05714286, 0.05      ])

» # operações entre arrays
» ar2 =  np.linspace(10, 50, 5)
» print(ar1)
» print(ar2)
↳ [10.  12.5 15.  17.5 20. ]
↳ [10. 20. 30. 40. 50.]

» ar1 + ar2
↳ array([20. , 32.5, 45. , 57.5, 70. ])

» ar1 * ar2
↳ array([ 100.,  250.,  450.,  700., 1000.])

» ar2 / ar1
↳ array([1.        , 1.6       , 2.        , 2.28571429, 2.5       ])

» # operações com arrays (2 × 3)
» ar3 = np.linspace(0,5, 6).reshape(2,3)
» ar4 = np.linspace(0,10, 6).reshape(2,3)

» print(ar3)
↳ [[0. 1. 2.]
   [3. 4. 5.]]

» print(ar4)
↳ [[ 0.  2.  4.]
   [ 6.  8. 10.]]

» ar3 + ar4
↳ array([[ 0.,  3.,  6.],
         [ 9., 12., 15.]])

» ar3 - ar4
↳ array([[ 0., -1., -2.],
         [-3., -4., -5.]])

» ar3 * ar4
↳ array([[ 0.,  2.,  8.],
         [18., 32., 50.]])
       
» # operações de incremento são realizados inplace
» ar3 +=1
» ar3
↳ array([[1., 2., 3.],
         [4., 5., 6.]])

» # seno e cosseno em np retorna um array e/e
» ar1 * np.sin(ar2)
↳ array([ -5.44021111,  11.41181563, -14.82047436,  13.03948031,
          -5.24749707])

» ar3 * np.cos(ar4)
↳ array([[ 0.        , -0.41614684, -1.30728724],
         [ 2.88051086, -0.58200014, -4.19535765]])

Comparações entre arrays resultam em arrays booleanos.

» ar5 = np.linspace(0,5, 6).reshape(2,3)
» ar6 = np.random.random(6).reshape(2,3).round(2)*5

» ar5
↳ array([[0., 1., 2.],
         [3., 4., 5.]])
» ar6
↳ array([[3.  , 2.45, 1.2 ],
         [3.1 , 1.55, 1.75]])

» arrMaior= ar5 > ar6
» arrMaior
↳ array([[False, False,  True],
         [False,  True,  True]])

Broadcasting: A operações feitas acima, entre um array e um escalar, transformam o escalar em um array de dimensões apropriadas (de mesmo shape) antes de sua realização. Essa operação se chama broadcasting:. Por exemplo:

» ar1 = np.array([0,1,2,3])
» ar2 = np.array([4,4,4,4])

» # a soma com um escalar
» ar1 + 4
↳ array([4, 5, 6, 7])

» # é  mesmo que
» ar1 + ar2
↳ array([4, 5, 6, 7])

» # os elementos são iguais
» ar1 + ar2 == ar1 + 4
↳ array([ True,  True,  True,  True])

# o mesmo ocorre com comparações
» ar1 ≥ 2
↳ array([False, False,  True,  True])

Uma forma de seleção diferente consiste em passar listas de valores como índices. O array retornado depende de como essas listas são passadas. Essa é técnica é chamada de fancy indexing (indexação sofisticada). Em qualquer dos casos abaixo os índices podem aparecer em qualquer ordem.

O slice array[[i,j,...]] contém as linhas array[i], array[j], etc. (O mesmo que array[:,[i,j,...]]).
O slice array[:,[i,j,...]] contém as colunas array[:,i], array[:,j], etc.
O slice array[[i,j,...]:[r, s,...]] é uma linha contendo os elementos array[i,r], array[j,s], etc.

» # fancy indexing (passando arrays como indices)
» # vamos construir um array 6 × 5 e atribuir seus valores um a um
» arr = np.empty((6,5))

» for linha in range(6):
»     for coluna in range(5):
»         arr[linha,coluna] = linha * 10 + coluna
        
» # o array obtido é (uma forma de identificar facilmente de que elemento se trata)
» arr
↳ array([[ 0.,  1.,  2.,  3.,  4.],
         [10., 11., 12., 13., 14.],
         [20., 21., 22., 23., 24.],
         [30., 31., 32., 33., 34.],
         [40., 41., 42., 43., 44.],
         [50., 51., 52., 53., 54.]])

» # podemos selecionar linhas (em qualquer ordem)
» arr[[3,5,1]]       # o mesmo que arr[[3,5,1],:]
↳ array([[30., 31., 32., 33., 34.],
         [50., 51., 52., 53., 54.],
         [10., 11., 12., 13., 14.]]) 

» # ou colunas (em qualquer ordem)
» arr[:,[3,1]]
↳ array([[ 3.,  1.],
         [13., 11.],
         [23., 21.],
         [33., 31.],
         [43., 41.],
         [53., 51.]])

» # fornecer duas listas (que devem ter o mesmo tamanho) tem efeito diferente,
» # retornando array de i dimensão com os índices dados nas listas
» arr[[0,3,4,1],[0,3,4,1]]
↳ array([ 0., 33., 44., 11.])

» arr[[0,3,4,1],[1,0,4,2]]
↳ array([ 1., 30., 44., 12.])

Funções universais

Funções universais, ou ufunc, são funções que agem e/e, sobre todos os elementos de um array, retornando outra array de mesmas dimensões. Essas operações são também chamadas de operações vetorializadas. Embora envolvam laços (loops ) esses são realizados internamente e de forma eficiente, de modo a agilizar os processos.

Uma tabela das funções universais é encontrada abaixo.

Método retorna
abs, fabs valor absoluto inteiros, floats, ou complexos
sqrt raiz quadrada (equivale a arr**0.5)
square elementos elevados ao quadrado (equivale a arr**2)
exp exponencial de cada elemento (ex)
log, log10, logaritmos naturais (de base e e base 10var>
log2, log1p logaritmos de base 2 e log(1 + x)
sign sinal: (1, 0, -1) (positivo, zero, negativo)
ceil teto, menor inteiro maior ou igual
floor piso, maior inteiro menor ou igual
rint arredonda para o inteiro mais próximo, preservando dtype
modf partes inteiras e fracionárias do array, em e arrays
isnan array booleano, se o valor é NaN (Not a Number)
isfinite array booleano, se cada valor é finito (non-inf, non-NaN)
isinf array booleano, se cada valor é infinito
cos, sin, tan funções trigonométricas
cosh, sinh, tanh funções trigonométricas hiperbólicas
arccos, arcsin, arctan arcos de funções trigonométricas
arccosh, arcsinh, arctanh arcos de funções trigonométricas hiperbólicas
logical_not array booleano, negação do array (equivalent to ~arr).

Exemplos de uso:

» # Funções universais
» arrBool = np.array([True, False, False, True])
» arrBool
↳ array([ True, False, False,  True])
» np.logical_not(arrBool)
↳ array([False,  True,  True, False])

» arr = np.linspace(0, 10, 6)
» arr -=5
» arr
↳ array([-5., -3., -1.,  1.,  3.,  5.])

» np.abs(arr)
↳ array([5., 3., 1., 1., 3., 5.])

» # não altera arr
» np.sign(arr)
↳ array([-1., -1., -1.,  1.,  1.,  1.])

» arr = arr/10 +4
» arr = arr.reshape(2,3)
» arr
↳ array([[3.5, 3.7, 3.9],
         [4.1, 4.3, 4.5]])

» np.modf(arr)
↳ (array([[0.5, 0.7, 0.9],
          [0.1, 0.3, 0.5]]),
↳  array([[3., 3., 3.],
          [4., 4., 4.]]))

Funções de Agregação


Funções de agregação são funções que realizam operações em todos os elementos do array, retornando um escalar(um número). Em sua maioria elas retornam cálculos estatíscos sobre os dados.

» ag = np.array([3.3, 12.5, 11.2, 5.7, 0.3])
» ag
↳ array([ 3.3, 12.5, 11.2,  5.7,  0.3])

» # outputs nos comentários
» ag.sum()       # 33.0
» ag.min()       # 0.3
» ag.max()       # 12.5
» ag.mean()      # 6.6
» ag.std()       # 4.6337889464238655
» ag.var()       # 21.472
» ag.argmin()    # 4
» ag.argmax()    # 1

» # o mesmo vale para arrays com outros shapes
» ag23 =  np.random.random(6).reshape(2,3) -.5
» ag23
↳ array([[ 0.10425075, -0.29335437, -0.36814244],
         [ 0.32986805,  0.17289794, -0.4568041 ]])

» ag23.mean()
↳ -0.08521402850598175

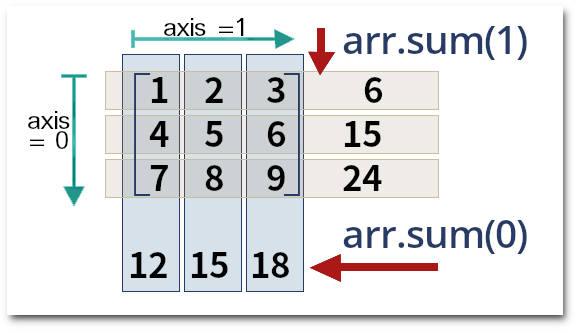
Diversas das operações podem ser feitas sobre o array inteiro ou sobre linhas ou colunas. Para isso podemos especificar axis = 0 para operações sobre elementos das colunas, axis = 1 para operações sobre elementos das linhas.

» arr = np.random.randn(4,5).round(2)
» arr
↳ array([[ 0.45, -0.11, -0.54, -0.97, -0.23],
         [ 1.65,  0.76, -0.39, -1.83,  0.02],
         [ 0.45, -1.22,  1.93,  1.92, -0.43],
         [-0.39,  2.01,  0.04,  0.67, -1.1 ]])

» # a soma de todos os elementos
» arr.sum()
↳ 2.689999999999999

» # soma sobre elementos de cada coluna
» arr.sum(axis=0)       # ou arr.sum(0)
↳ array([ 2.17,  0.37,  0.17, -2.49, -3.13])

» # soma sobre elementos de cada linha
» arr.sum(axis=1)       # ou arr.sum(1)
↳ array([-0.42, -1.67,  0.6 , -1.42])

» # produtos dos elementos das linhas
» arr.prod(axis=1).round(2)
↳ array([0.01, 0.02, 0.87, 0.02])

» # produtos dos elementos das colunas
» arr.prod(axis=0).round(2)
↳ array([-0.13,  0.21,  0.02,  2.28, -0.  ])


Funções básicas de agregação:

Função retorna
np.all booleano, True se todos os elementos no array são não nulos
np.any booleano, True se algum dos elementos no array é não nulo
np.sum soma dos elementos do array ou sobre eixo especificado †.
np.mean Média aritmética; arrays de comprimento nulo têm média = NaN
np.std, np.var variância e desvio padrão
np.max, np.min valor máximo e mínimo no array
np.argmax, np.argmin índices do valor máximo e mínimo no array
np.cumsum soma cumulativa dos elementos, começando em 0
np.cumprod produto cumulativo dos elementos, começando em 1

(†) Para arrays de comprimento nulo tem soma np.sum = NaN.

🔺Início do artigo

Bibliografia

  • Blair, Steve: Python Data Science, edição do autor, 2019.
  • Harrison, Matt: Learning Pandas, Python Tools for Data Munging, Data Analysis, and Visualization,
    Treading on Python Series, Prentiss, 2016.
  • Johansson, Robert: Numerical Python, Scientific Computing and Data Science Applications with Numpy, SciPy and Matplotlib, 2nd., Chiba, Japan, 2019.
  • McKinney, Wes: Python for Data Analysis, O’Reilly Media, Sebastopol CA, 2018.
  • McKinney, Wes, Pandas Development Team: pandas: powerful Python data analysis toolkit Release 1.2.1,
  • Miller, Curtis: Hands-On Data Analysis with NumPy and pandas, Packt Publishing, Birmingham, 2018.
  • Nelli, Fabio: Python Data Analytics With Pandas, NumPy, and Matplotlib, 2nd., Springer, New York, 2018.
  • Site AI Ensina: Entendendo a biblioteca NumPy, acessado em julho de 2021.
  • Site GeeksforGeeks: Python NumPy, acessado em julho de 2021.
  • Site W3 Schools: NumPy Tutorial, acessado em julho de 2021.
  • NumPy, docs.
  • NumPy, Learn.

Nesse site:

Introdução ao Pandas – Series

Posted on by Guilherme

🔻Final do artigo

O que é pandas?

Leia nesse site:
Jupyter Notebook,
Linguagem de Consultas SQL,
Pandas e SQL comparados.

Pandas é uma biblioteca do Python, de código aberto e com licença BSD, desenvolvida e mantida pelo PуDаtа Dеvеlорmеnt Tеаm. Ela fornece ferramentas de manipulação e análise estatística de dados, capacidade de exibição gráfica E extração de dados análogos (mas não idênticos) aos de consultas sql.

A biblioteca foi construída com Cython e, por isso, é bastante rápida. Ela se destinava inicialmente ao uso no setor financeiro para análise de séries temporiais, tendo se tornado uma ferramenta de uso comum na manipulação de dados, particularmente em data science e machine learning. Ela tem sido usada para substituir as planilhas do Excel, para processar dados sob forma tabular, importando com facilidade dados de arquivos csv ou json.

Os experimentos abaixo foram realizados no Jupyter Notebook. Você encontra nesse site um artigo sobre instalação e uso do Jupyter Notebook. As linhas de código e suas respostas, quando existirem, serão representadas da seguinte forma:

» # Comentários (não são lidos ou executados pelo interpretador)
» Linha de input (entrada de comandos)
↳ Linha de output (resposta do código)

NumPy e matplotlib

NumPy é a abreviação de Numerical Python, a biblioteca base da computação numérica em Python. Ela fornece as estruturas de dados e algoritmos necessários para a maioria das aplicações científicas e de engenharia utilizando cálculo numérico. Entre outros objetos NumPy NumPy fornece

  • o objeto multidimensional ndarray onde se pode aplicar operações vetorializadas rápidas e eficientes,
  • um conjunto de funções para cálculos elementares com vetores e matrizes,
  • ferramentas de leitura e gravação de dados,
  • operações da álgebra linear, transformada de Fourier e geração de números aleatórios,
  • interação com C e C++.


Para dados numéricos as matrizes do NumPy são armazenadas e manipuladas de modo mais eficiente do que as demais estruturas do Python. Além disso códigos escritos em linguagens de baixo nível, como C ou Fortran, podem operar diretamente nos dados armazenados com o NumPy. Por isso muitas ferramentas de computação numérica do Python usam as matrizes NumPy como um estrutura de dados primária.

matplotlib é a biblioteca Python mais popular usada para a produção de gráficos e visualização de dados. Ela pode ser usada na geração de gráficos estáticos ou animados e visualização interativa.

Pandas

O pandas se utiliza basicamente de 3 objetos de armazenamento de dados com as seguintes estruturas:
Estrutura de dados dos objetos do pandas:

Nome dimensões tabela
Series 1D coluna (vetor)
DataFrame 2D tabela (matriz)
Panel 3D várias tabelas (matriz multidimensional)

As series e os dataframes são utilizados com maior frequência.

Como a manipulação de dados usando séries e dataframes frequentemente envolvem operações encontradas no módulo numpy é frequente sua importação junto com pandas.

» import pandas as pd
» import numpy as np

Series

Uma series é um objeto unidimensional, tipo um vetor, que contém uma sequência de objetos do mesmo tipo. A essa sequência está associado um outro vetor de labels chamado de index (índice). O método básico de criação de séries é da seguinte forma:
serie = pd.Series(data, index=index)
onde data pode ser um dict (um dicionário do Python), uma lista ou ndarray do numPy, ou um escalar. index é uma lista de índices que, se omitida, é preenchida com inteiros iniciando em 0.

» serie1 = pd.Series([-1, 9, 0, 2, 5])
↳  0   -1
   1    9
   2    0
   3    2
   4    5

À esquerda estão listados os índices que, por default, são uma lista de inteiros começando por 0. Os valores podem ser listados com .values e os índices com .index.

» serie1.values
↳ array([-1,  9,  0,  2,  5])

» serie1.index
↳ RangeIndex(start=0, stop=5, step=1)

Os índices podem ser inseridos manualmente e não precisam ser inteiros. O valor correspondente ao índice i pode ser acessado com serie[i], como mostrado abaixo, onde os índices são strings.

» serie2 = pd.Series([4, 7, -5, 3], index=['a', 'b', 'c', 'd'])
» serie2
↳ a    4
  b    7
  c   -5
  d    3
  dtype: int64

» serie2['c']
↳ -5

Uma série pode ser filtrada passando como índice outra série de elementos boolenos, (True, False). Além disso operações vetorializadas podem ser realizadas sobre todos os elementos da série.

# O teste seguinte gera uma série de booleanos
» serie2 > 3
↳ a     True
  b     True
  c    False
  d    False
  dtype: bool

# Essa serie de True e False filtra a serie original
» serie2[serie2 > 3]
↳ a    4
  b    7
  dtype: int64

# Operações podem, ser realizadas sobre todos os elementos
» serie2 * 3
↳ a    12
  b    21
  c   -15
  d     9
  dtype: int64

# o módulo Numpy possui a função exponencial
» np.exp(serie2)
↳ a      54.598150
  b    1096.633158
  c       0.006738
  d      20.085537
  dtype: float64

Séries se comportam, em muitos sentidos, como um dicionário. Uma série pode ser criada passando-se um dicionário como argumento para pd.Series().

» populacao = {
           'Sudeste': 89012240, 
           'Nordeste': 57374243,
           'Sul': 30192315,
           'Norte': 18672591,
           'Centro-Oeste':16504303
         }

» serie3 = pd.Series(populacao)

» serie3
↳ Sudeste         89012240
  Nordeste        57374243
  Sul             30192315
  Norte           18672591
  Centro-Oeste    16504303
  dtype: int64


A ordem dos itens na série pode ser alterada através do fornecimento de uma lista com o ordenamento desejado para o argumento index. A elementos não presentes no dicionário serão atribuídos o valor NaN, Not a Number (não número). O método pd.isnull(serie) permite a avalição de quais elementos estão nulos ou NaN.

# fornecendo uma lista para o argumento index:
» ordem_alfabetica = ['Brasil', 'Centro-Oeste', 'Nordeste', 'Norte', 'Sudeste', 'Sul']
» serie4 = pd.Series(populacao, index=ordem_alfabetica)
» serie4
↳ Brasil               NaN
  Centro-Oeste    16504303
  Nordeste        57374243
  Norte           18672591
  Sudeste         89012240
  Sul             30192315
  dtype: int64

# para verificar quais valores são nulos (NaN)
» pd.isnull(serie4)
↳ Brasil           True
  Centro-Oeste    False
  Nordeste        False
  Norte           False
  Sudeste         False
  Sul             False
  dtype: bool

# os seguintes registros são NaN
» serie4[pd.isnull(serie4)]
↳ Brasil   NaN
  dtype: float64

» serie4[pd.notnull(serie4)]
↳ Centro-Oeste    16504303.0
  Nordeste        57374243.0
  Norte           18672591.0
  Sudeste         89012240.0
  Sul             30192315.0
  dtype: float64

» 'Brasil' in serie4
↳ True
» 'EUA' in serie4
↳ False
# uma excessão KeyError é lançada se o indice não existe
» serie4['EUA']
↳ KeyError

Como não existe no dicionário um valor para o índice Brasil a série atribuiu o valor NaN (Not a Number) para essa chave, a forma de NumPy e pandas indicar a ausência de um valor. O método retorna True ou False para cada item da série e pd.notnull() o seu inverso booleano. Alternativamente se pode usar o método das séries serie4.isnull().

Ainda sobre a semelhança entre séries e dicionários, podemos testar a existência de uma chave usando o operador in, como em 'Brasil' in serie4. A tentativa de recuperar um valor com índice não existente gera uma exceção (um erro do Python).

Observe que uma series tem propriedades de numpy ndarray, mas é um objeto de tipo diferente. Se um ndarray é necessário use series.to_numpy().

» type(serie4)
↳ pandas.core.series.Series

» type(serie4.to_numpy())
↳ numpy.ndarray

Series podem ser fatiadas com a notação serie[i:f] onde serão retornadas a i-ésima linha até a f-ésima, exclusive. Se i for omitido a lista se inicia em 0, se f for omitido ela termina no final da series.

» serie4
↳ Brasil                 NaN
  Centro-Oeste    16504303.0
  Nordeste        57374243.0
  Norte           18672591.0
  Sudeste         89012240.0
  Sul             30192315.0
  dtype: float64

» serie4[2:5]
↳ Nordeste        57374243.0
  Norte           18672591.0
  Sudeste         89012240.0
  dtype: float64

» serie4[:2]
↳ Brasil                 NaN
  Centro-Oeste    16504303.0
  dtype: float64

» serie4[4:]
↳ Sudeste    89012240.0
  Sul        30192315.0
  dtype: float64

Series podem ser exibidas com o método display(serie_0, serie_1, ..., serie_n). O resultado de operações envolvendo mais de uma serie, como a soma, alinha os valores por chaves (como uma UNION). Valores não presentes em um dos operandos terá NaN como resultado.

» serie5 = pd.Series([2, -1, -2, 1], index=['a', 'b', 'c', 'd'])
» serie6 = pd.Series([3, 4, 7, -1], index=['e', 'c', 'b', 'f'])
» display(serie5, serie6)
↳ a    2
  b   -1
  c   -2
  d    1
  dtype: int64

↳ e    3
  c    4
  b    7
  f   -1
  dtype: int64

» serie5 + serie6
↳ a    NaN
  b    6.0
  c    2.0
  d    NaN
  e    NaN
  f    NaN
  dtype: float64

Series possuem a propriedade name que pode ser atribuída na construção ou posteriormente com o método .rename(). No exemplo usamos o método np.random.randn(n) de numpy para fornecer um numpy.ndarray com n números aleatórios. Damos inicialmente a essa série o nome ‘randomica’, depois a renomeamos para ‘aleatoria’.

» serie7 = pd.Series(np.random.randn(5), name='randomica')
» serie7
↳ 0   -1.703662
  1    1.406167
  2    0.966557
  3   -0.557846
  4   -0.264914
  Name: randomica, dtype: float64

» serie7.name
↳ 'randomica'

» serie7= serie7.rename('aleatoria')
» serie7.name
↳ 'aleatoria'

O nome de uma série se torna seu índice ou nome de coluna caso ela seja usada para formar um DataFrame.

Atributos e Métodos das Series

Os atributos e métodos mais comuns e úteis das Series estão listados abaixo. Para uma lista completa consulte pandas.Series: API Reference.

Atributos

Atributo Descrição
at[n] Acesso ao valor na posição n
attrs Retorna ditionario de atributos globais da series
axes Retorna lista de labels do eixo das linhas
dtype Retorna o tipo (dtype) dos objetos armazenados
flags Lista as propriedades do objeto
hasnans Informa se existem NaNs
iat[n] Acesso ao valor na posição n inteiro
iloc[n] Acesso ao valor na posição n inteiro
index Retorna lista de índices
index[n] Retorna índice na n-ésima posição
is_monotonic Booleano: True se valores crescem de forma monotônica
is_monotonic_decreasing Booleano: True se valores decrescem de forma monotônica
is_unique Booleano: True se valores na series são únicos
loc Acessa linhas e colunas por labels em array booleano
name O nome da Series
nbytes Número de bytes nos dados armazenados
shape Retorna uma tuple com forma (dimensões) dos dados
size Número de elementos nos dados
values Retorna series como ndarray

Alguns casos de acessos à essas propriedades. Os outputs são exibidos como comentários:

» import pandas as pd
» import numpy as np 
» serie = pd.Series([1,-1, 2, 2, 6, 63])
» serie.size              # 6, o mesmo que len(serie)
» serie.at[5]             # 63
» serie.iloc[0]           # 1
» serie.index             # RangeIndex(start=0, stop=6, step=1)
» serie.is_monotonic      # False
» serie.is_unique         # False
» serie.shape             # (6,)

Métodos

Nas tabelas abaixo a expressão “elemento a elemento” é abreviada para “e/e”. Estas operações são repetidas a cada elemento da, ou das, séries envolvidas. Por exemplo, o método serie.add(s2) é feita “elemento a elemento” (e/e):

» import pd	
» serie_a = pd.Series([-1,9,0,2, 5, -8])
» serie_b = pd.Series([1,-9,0, -2,-5, 8])
» serie_a.add(serie_b)
» # é o mesmo que
» serie_a + serie_b
» # que resulta em serie nula 
» # pd.Series([0,0,0,0,0,0])

Manipulação e gerenciamento das Series

Método (sobre série s, outra s2) Descrição
s.align(s2) Alinha 2 objetos em seus eixos usando método especificado
s.append(to_append[, ignore_index, …]) Concatena 2 ou mais Series
s.asof(where[, subset]) Último elemento antes da ocorrência de NaNs após ‘where’
s.backfill([axis, inplace, limit, downcast]) Aliás para DataFrame.fillna() usando method=’bfill’
s.bfill([axis, inplace, limit, downcast]) Alias para DataFrame.fillna() usando method=’bfill’
s.clip([min, max, axis, inplace]) Inclui apenas valores no intervalo
s.combine(s2, func[, fill_value]) Combina a s com s2 ou escalar, usando func
s.copy([deep]) Cópia do objeto s, índices e valores
s.drop_duplicates([keep, inplace]) Remove elementos duplicados de s
s.dropna() Remove valores faltantes de s
s.duplicated([keep]) Exibe valores duplicados na s
s.explode([ignore_index]) Transforma cada elemento de um objeto tipo lista em uma linha
s.fillna([value, method, axis, inplace, …]) Substitui valores NA/NaN usando método especificado
s.get(key) Retorna item correspondente à key
s.groupby([by, axis, level, as_index, sort, …]) Agrupa a s
s.head([n]) Retorna os n primeiros valores
s.interpolate([method, axis, limit, inplace, …]) Preenche valores NaN usando metodo de interpolação
s.item() Primeiro elemento dos dados como escalar do Python
s.items() Iteração (lazy) sobre a tupla (index, value)
s.iteritems() Iteração (lazy) sobre a tupla (index, value)
s.mask(cond[, s2, inplace, axis, level, …]) Substitui valores sob condição dada
s.max([axis, skipna, level, numeric_only]) Valor máximo
s.memory_usage([index, deep]) Memória usada pela s
s.min([axis, skipna, level, numeric_only]) Menor dos valores da s
s.nlargest([n, keep]) Retorna os n maiores elementos
s.nsmallest([n, keep]) Retorna os n menores elementos
s.nunique([dropna]) Retorna quantos elementos únicos existem na s
s.pad([axis, inplace, limit, downcast]) O mesmo que DataFrame.fillna() usando method=’ffill’
s.plot() O mesmo que pandas.plotting._core.PlotAccessor
s.pop(i) Remove s[i] de s e retorna s[i]
s.repeat(repeats[, axis]) Repete elementos da s
s.replace([to_replace, value, inplace, limit, …]) Substitui valores em to_replace por value
s.sort_values([axis, ascending, inplace, …]) Reorganiza s usando seus valores
s.str Usa funções de string sobre s (se string). Ex. s.str.split(“-“)
s.tail([n]) Últimos n elementos
s.unique() Retorna os valores da s, sem repetições
s.update(s2) Modifica s usando valores de s2, usando índices iguais
s.view([dtype]) Cria uma nova “view” da s
s.where(cond[, serie, inplace, axis, level, …]) Substitui valores se a condição cond = True

Operações matemáticas básicas:

s.ewm([com, span, halflife, alpha, …])Calcula exponencial com peso

s.abs() Retorna s com valor absoluto, e/e
s.add(s2) Soma s com s2, e/e
s.agg([func, axis]) Agrega usando func sobre o eixo especificado
s.apply(func[, convert_dtype, args]) Aplica func sobre os valores de s, e/e
s.div(s2) Divisão (float) de s por s2, e/e
s.divmod(s2) Divisão inteira e módulo de s por s2, e/e
s.dot(s2) Produto interno entre a s e s2
s.floordiv(s2) Divisão inteira da s por s2, e/e
s.mod(s2[, level, fill_value, axis]) Módulo de s por s2, e/e
s.rfloordiv(s2[, level, fill_value, axis]) Divisão inteira de s por s2, e/e
s.rmod(s2[, level, fill_value, axis]) Modulo da divisão da s por s2, e/e
s.rmul(s2[, level, fill_value, axis]) Multiplicação de s por s2, e/e
s.round([n]) Arredonda valores da s para n casas decimais.
s.rpow(s2[, level, fill_value, axis]) Exponential de s por s2, e/e
s.rsub(s2[, level, fill_value, axis]) Subtração da s por s2, e/e
s.rtruediv(serie[, level, fill_value, axis]) Divisão (float) de s por s2, e/e
s.sub(s2) Subtração de s por s2, e/e
s.subtract(serie) Idem
s.sum([axis, skipna, level, numeric_only, …]) Soma dos valores da s
s.transform(func[, axis]) Executa func sobre elementos de s
s.truediv(s2) Divisão (float) de s por s2, e/e
s.truncate([before, after, axis, copy]) Trunca a s antes e após índices dados
s.mul(s2[, level, fill_value, axis]) Multiplicação de s por s2, e/e
s.multiply(s2[, level, fill_value, axis]) Idem
s.pow(s2) Exponential de s por s2, e/e
s.prod([axis, skipna, level, numeric_only, …]) Produto dos elementos da s
s.product([axis, skipna, level, numeric_only, …]) Idem
s.rdiv(s2[, level, fill_value, axis]) Divisão (float) de s por s2, e/e
s.rdivmod(s2) Divisão inteira e módulo de s por s2, e/e

Operações estatísticas:

Método (sobre série s, outra s2) Descrição
s.corr(s2) Correlação de s com s2, excluindo NaNs
s.count([level]) Número de observações na s, excluindo NaN/nulls
s.cov(s2[, min_periods, ddof]) Covariância da s, excluindo NaN/nulls
s.cummax([axis, skipna]) Máximo cumulativo
s.cummin([axis, skipna]) Mínimo cumulativo
s.cumprod([axis, skipna]) Produto cumulativo
s.cumsum([axis, skipna]) Soma cumulativa
s.describe([percentiles, include, exclude, …]) Gera descrição estatística
s.kurt([axis, skipna, level, numeric_only]) Kurtosis imparcial
s.kurtosis([axis, skipna, level, numeric_only]) Idem
s.hist() Plota histograma da s usando matplotlib.
s.mad([axis, skipna, level]) Desvio médio absoluto dos valores de s
s.mean([axis, skipna, level, numeric_only]) Média dos valores
s.median([axis, skipna, level, numeric_only]) Mediana dos valores
s.mode([dropna]) Moda da s
s.quantile([q, interpolation]) Valor no quantil dado
s.ravel([order]) Retorna dados como um ndarray
s.sample([n, frac, replace, weights, …]) Amostra randomizada de items da s
s.sem([axis, skipna, level, ddof, numeric_only]) Erro padrão imparcial da média
s.skew([axis, skipna, level, numeric_only]) Inclinação imparcial
s.std([axis, skipna, level, ddof, numeric_only]) Desvio padrão da amostra
s.value_counts([normalize, sort, ascending, …]) Retorna s com a contagem de valores únicos
s.var([axis, skipna, level, ddof, numeric_only]) Variância imparcial dos valores da s

Operações com índices:

s.add_prefix('prefixo') Adiciona prefixo aos labels com string ‘prefixo’
s.add_suffix('sufixo') Adiciona sufixo aos labels com string ‘sufixo’
s.argmax([axis, skipna]) Posição (índice inteiro) do valor mais alto de s
s.argmin([axis, skipna]) Posição (índice inteiro) do menor valor de s
s.argsort([axis, kind, order]) Índices inteiros que ordenam valores da s
s.drop([labels]) Retorna s com labels removidos
s.first_valid_index() Índice do primeiro valor não NA/null
s.idxmax([axis, skipna]) Label do item de maior valor
s.idxmin([axis, skipna]) Label do item de menor valor
s.keys() Alias de index
s.last_valid_index() Índice do último valor não NA/null
s.reindex([index]) Ajusta a s ao novo índice
s.reindex_like(s2[, method, copy, limit, …]) Série com índices em acordo com s2
s.rename([index, axis, copy, inplace, level, …]) Altera o nome (labels) dos índices
s.reorder_levels(order) Reajusta níveis de índices usando order
s.reset_index([level, drop, name, inplace]) Reinicializa índices
s.searchsorted(value[, side, sorter]) Índices onde elementos devem ser inseridos para manter ordem
s.sort_index([axis, level, ascending, …]) Reorganiza s usando os índices

Testes, com retorno booleanos e comparações:

Método (sobre série s, outra s2) Descrição
s.all([axis, bool_only, skipna, level]) Booleano: se todos os elementos são True
s.any([axis, bool_only, skipna, level]) Booleano: se algum elemento é True
s.equals(s2) Booleano: True se s contém os mesmos elementos que s2
s.between(min, max) Booleano: satisfazendo min <= s <= max, e/e
s.compare(s2[, align_axis, keep_shape, …]) Compara s com s2 exibindo diferenças
s.eq(s2) Boleano: igualdade entre s e s2, e/e
s.ge(s2) Booleana: maior ou igual entre s e s2, e/e
s.gt(s2[, level, fill_value, axis]) Booleana: se s é maior que s2, e/e
s.isin(valores) Booleano: se elementos da s estão contidos em valores
s.isna() Booleano: se existem valores ausentes
s.isnull() Booleano: se existem valores nulos
s.le(s2) Booleana: se s é menor ou igual a s2, e/e
s.lt(s2[, level, fill_value, axis]) Booleana: se s é menor que s2, e/e
s.ne(s2[, level, fill_value, axis]) Booleana: se s é diferente de s2, e/e
s.notna() Booleana: se existem valores não faltantes ou nulos
s.notnull() Idem

Transformações para outros formatos e tipos:

s.astype(dtype[, copy, errors]) Transforma (cast) para dtype
s.to_clipboard([excel, sep]) Copia o object para o clipboard do sistema
s.to_csv([path_or_buf, sep, na_rep, …]) Grava a s como arquivo csv
s.to_dict() Converte s para dict {label ⟶ value}
s.to_excel(excel_writer[, sheet_name, na_rep, …]) Grava s como uma planilha Excel
s.to_frame([name]) Converte s em DataFrame
s.to_hdf(path_or_buf, key[, mode, complevel, …]) Grava s em arquivo HDF5 usando HDFStore
s.to_json([path_or_buf, orient, date_format, …]) Converte s em string JSON
s.to_latex([buf, columns, col_space, header, …]) Renderiza objeto para LaTeX
s.to_markdown([buf, mode, index, storage_options]) Escreve a s em formato Markdown (leia)
s.to_numpy([dtype, copy, na_value]) Converte s em NumPy ndarray
s.to_pickle(path[, compression, protocol, …]) Grava objeto serializado em arquivo Pickle
s.to_sql(name, con[, schema, if_exists, …]) Grava elementos em forma de um database SQL
s.to_string([buf, na_rep, float_format, …]) Constroi uma representação string da s
s.tolist() Retorna uma lista dos valores
s.to_list() idem

Operações com séries temporais:

s.asfreq(freq) Converte TimeSeries para frequência especificada.
s.at_time(time[, asof, axis]) Seleciona valores em determinada hora (ex., 9:30AM)
s.between_time(inicio, fim) Seleciona valores com tempo entre inicio e fim
s.first(offset) Seleciona período inicial de uma série temporal usando offset.
s.last(offset) Seleciona período final de uma série temporal usando offset

Alguns exemplos de uso dos métodos de pandas.Series:

» import pandas as pd
» import numpy as np
» serie = pd.Series([1,-1, 2, 2, 6, 63])
» serie.abs()
» # retorna  pd.Series([1, 1, 2, 2, 6, 63])

» # Muitos métodos não alteram a series inplace.
» s2 = serie.rename('NovoNome')  # não altera nome de serie
» s2.name
↳ 'NovoNome'
» # para alterar o nome usamos
» serie.rename('NovoNome', inplace=True)  # altera nome de serie inplace
» serie.name
↳ 'NovoNome'

» # um resumo estatístico pode ser visto com describe
» serie.describe()
↳ count    15.000000
  mean      4.866667
  std       3.044120
  min       0.000000
  25%       3.500000
  50%       5.000000
  75%       7.000000
  max       9.000000
  dtype: float64

» # gerando outra series
» data = np.random.randint(0, 10,size=15)
» serie2 = pd.Series(data)
» data
↳ array([2, 2, 6, 3, 1, 4, 3, 4, 3, 0, 8, 3, 8, 2, 7])

» serie.div(serie2)
↳ 0     2.500000
  1     0.000000
  ...
  9          inf
  13    0.000000
  14    1.000000
  dtype: float64


Observe que a divisão por 0 não gera erro mas é representada por inf.

Alguma habilidade gráfica pode ser encontrada entre os métodos das series. Um exemplo é o serie.hist() que traça o histograma da series usando matplotlib. Veremos com mais detalhes as funcionalidades dessa biblioteca.

» data = np.random.randint(0, 10,size=15)
» data
array([5, 0, 7, 7, 0, 9, 6, 5, 6, 9, 5, 5, 2, 0, 7])
» serie = pd.Series(data)
» serie.hist()

Objetos do pandas possuem métodos poderosos e eficientes. O método serie.str() permite operações de strings sobre os elementos da serie, se esses forem strings.

» str = ['-mercado','-tensão','-plasia']
» serie = pd.Series(str)
» serie
↳ 0    -mercado
  1     -tensão
  2     -plasia

» serie = serie.str.replace('-','hiper-')
» serie
↳ 0    hiper-mercado
  1     hiper-tensão
  2     hiper-plasia

» serie.str.split('-')
↳ 0    [hiper, mercado]
  1     [hiper, tensão]
  2     [hiper, plasia]

» # elementos não strings resultam em NaN
» serie = pd.Series([123,'-tensão','-plasia'])
» serie.str.replace('-','hiper-')
↳ 0             NaN
  1    hiper-tensão
  2    hiper-plasia

Series podem ser usadas na construção de dataframes, que serão vistos a seguir. Em particular o método to_frame() transforma uma series em um dataframe com uma coluna, onde cada valor ocupa uma linha.

» # uma series pode ser transformada em um dataframe
» df = serie.to_frame()
» # um dataframe é gerado e armazenado em df

Como a maioria dos métodos de series são análogos àqueles de dataframes faremos uma exploração mais extensa desses na sessão referente aos dataframes.

🔺Início do artigo

Bibliografia

  • Blair,Steve: Python Data Science, The Ultimate Handbook for Beginners on How to Explore NumPy for Numerical Data, Pandas for Data Analysis, IPython, Scikit-Learn and Tensorflow for Machine Learning and Business, edição do autor disponível na Amazon, 2019.
  • Harrison, Matt: Learning Pandas, Python Tools for Data Munging, Data Analysis, and Visualization,
    edição do autor, 2016.
  • McKinney, Wes: pandas: powerful Python data analysistoolkit, Release 1.2.1
    publicação do Pandas Development Team, revisado em 2021.
  • McKinney, Wes: Python for Data Analysis, Data Wrangling with Pandas, NumPy,and IPython
    O’Reilly Media, 2018.
  • Pandas: página oficial, acessada em janeiro de 2021.
  • Pandas User Guide, acessada em fevereiro de 2021.
  • Miller, Curtis: On Data Analysis with NumPy and pandas, Packt Publishing, Birmingham, 2018.