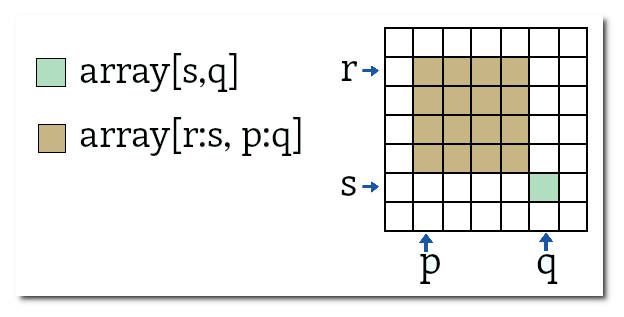Preparação de dados
Programadores que lidam com análise de dados passam grande parte do tempo dedicado a um projeto preparando esses dados, antes mesmo de começar qualquer análise. Normalmente os dados são importados de uma fonte externa, tal como um arquivo em forma tabular em html, pdf, texto puro ou csv. Eles precisam ser convertidos para um formato legível e muitas vezes contém erros e valores ausentes. A vezes o próprio processo de conversão introduz perda de dados, tal como acontece em textos impressos transformados em texto digital por OCR (optical character recognition ). Seja qual for a origem dos dados algum trabalho de depuração deve ser feito. Em seguida eles devem passar por formatação adequada, a quebra de tabelas, o estabelecimento de vínculos entre elas, etc. Pandas oferece boas ferramentas para todas essas etapas.

Dados ausentes
Já vimos que dados não presentes em alguma tabela são representados por NaN (not a number). O objeto None do python também é tratado como um valor ausente ou NA (not available). O método dropna() descarta linhas (se axis=0, default) ou colunas (se axis=1) contendo campos nulos. dropna(how='all') descarta linhas ou colunas se todos os campos forem nulos. Também podemos determinar que apenas linhas ou colunas com um número mínimo de elementos não nulos sejam mantidas, com df.dropna(thresh=n).
» import pandas as pd » import numpy as np » dados = pd.Series([121.45, np.nan ,32.12,42.21,51.56]) » dados ↳ 0 121.45 1 NaN 2 32.12 3 42.21 4 51.56 » dados[3]= None » dados.isnull() ↳ 0 False 1 True 2 False 3 True 4 False » dados.dropna() # o mesmo que dados[dados.notnull()] ↳ 0 121.45 2 32.12 4 51.56 » from numpy import nan as NA # para estabelecer um alias curto para np.nan » data = pd.DataFrame([[1., 6.5, 3.9], [1.3, NA, NA], [NA, NA, NA], [NA, 5.8, 6.7]]) » data ↳ 0 1 2 0 1.0 6.5 3.9 1 1.3 NaN NaN 2 NaN NaN NaN 3 NaN 5.8 6.7 » data.dropna() ↳ 0 1 2 0 1.0 6.5 3.9 » data.dropna(how='all') ↳ 0 1 2 0 1.0 6.5 3.9 1 1.3 NaN NaN 3 NaN 5.8 6.7 » data[4] = NA » data ↳ 0 1 2 4 0 1.0 6.5 3.9 NaN 1 1.3 NaN NaN NaN 2 NaN NaN NaN NaN 3 NaN 5.8 6.7 NaN » data.dropna(axis=1, how='all') ↳ 0 1 2 0 1.0 6.5 3.9 1 1.3 NaN NaN 2 NaN NaN NaN 3 NaN 5.8 6.7
Preenchendo valores ausentes
![]() A invés de descartar linhas e colunas com campos ausentes podemos preencher estas lacunas.
A invés de descartar linhas e colunas com campos ausentes podemos preencher estas lacunas. df.fillna(const) substitui campos NA com o valor único const. Um dicionário {coluna:valor} pode ser passado contendo constantes diferentes para cada coluna. Observando que df.mean() retorna uma Series com as médias de cada colunas, podemos usar df.fillna(df.mean()) para preencer NAs de cada coluna com essa média. Também podemos passar o parâmetro df.fillna(method='ffill') para preencher cada NA com o valor que o antecede na coluna. df.fillna(method='bfill') preenche NAs com o valor que o segue.
» # criando um df de teste com campos NA
» df = pd.DataFrame(np.random.randn(4, 3))
» df.iloc[0:3, 1] = NA
» df.iloc[1:3, 2] = NA
» df
↳ 0 1 2
0 0.615016 NaN -0.860821
1 1.195041 NaN NaN
2 -0.110482 NaN NaN
3 1.837690 1.569459 0.891858
» # preenche NAs com 0
» df.fillna(0)
↳ 0 1 2
0 0.615016 0.000000 -0.860821
1 1.195041 0.000000 0.000000
2 -0.110482 0.000000 0.000000
3 1.837690 1.569459 0.891858
» # preenche coluna 1 com 10, coluna 2 com 20
» df.fillna({1:10, 2:20})
↳ 0 1 2
0 0.615016 10.000000 -0.860821
1 1.195041 10.000000 20.000000
2 -0.110482 10.000000 20.000000
3 1.837690 1.569459 0.891858
» df.fillna(method='ffill')
↳ 0 1 2
0 0.615016 NaN -0.860821
1 1.195041 NaN -0.860821
2 -0.110482 NaN -0.860821
3 1.837690 1.569459 0.891858
» df.fillna(method='bfill')
↳ 0 1 2
0 0.615016 1.569459 -0.860821
1 1.195041 1.569459 0.891858
2 -0.110482 1.569459 0.891858
3 1.837690 1.569459 0.891858
» df.fillna(method='bfill', limit=2)
» df.mean()
↳ 0 0.884316
1 1.569459
2 0.015519
» df.fillna(df.mean())
↳ 0 1 2
0 0.615016 NaN -0.860821
1 1.195041 1.569459 0.891858
2 -0.110482 1.569459 0.891858
3 1.837690 1.569459 0.891858
Vemos que df.fillna(method='ffill') não substituiu valores nas linhas 0, 1, 2 da coluna 1 pois nenhum valor os antecede. Nesse caso teríamos que usar method='bfill', ou outra forma de preencher o campo vazio.
Substituições com dataframe.replace()
O método df.replace() substitui valores específicos em uma Series ou dataframe. Por ex., suponha que temos uma Series de valores positivos e a inserção de negativos foi convencionada para indicar valores ausentes. Podemos alterar esses valores usando df.replace(), lembrando que nenhuma das formas abaixo altera a Serie original, a menos que inplace=True seja usado.
» serie = pd.Series([12,-2, 34, -1]) » serie ↳ 0 12 1 -2 2 34 3 -1 » serie.replace(-2, -90) ↳ 0 12 1 -90 2 34 3 -1 » serie.replace([-2,-1], [20,10]) ↳ 0 12 1 20 2 34 3 10 » serie.replace(-1, NA) ↳ 0 12.0 1 -2.0 2 34.0 3 NaN
Claro que df.replace() pode ser usado para substituir um valor específico por valores calculados, usando métodos mais sofisticados de avaliação.
Em um dataframe df.replace(lista1, lista2) pode ser usado para substituir valores da lista1 pelos da lista2 (que deve ter o mesmo tamanho). df.replace(lista, escalar) substitui todos os valores em lista pelo escalar e df.replace(dicionario) substitui as chaves pelas valores no dicionário.
» df = pd.DataFrame({'a':[9,56,67], 'b':[33,55,66], 'c':[63,69,67], 'd':[2,3,9]})
» df
↳ a b c d
0 9 33 63 2
1 56 55 69 3
2 67 66 67 9
» df.replace(9, 100)
↳ a b c d
0 100 33 63 2
1 56 55 69 3
2 67 66 67 100
» df.replace([9, 55, 67], 0)
↳ a b c d
0 0 33 63 2
1 56 0 69 3
2 0 66 0 0
» df.replace([9, 55, 67], [1,2,3])
↳ a b c d
0 1 33 63 2
1 56 2 69 3
2 3 66 3 1
» df.replace({9:-9, 33:-33})
↳ a b c d
0 -9 -33 63 2
1 56 55 69 3
2 67 66 67 -9
Análise de outliers
Em qualquer processo de tomada de medidas ou coleta de dados existem restrições à precisão obtida. Mas, além da precisão restrita, é frequente existirem dados muito fora de qualquer curva esperada. Esses são os chamados pontos fora da curva ou outliers e geralmente são descartados. Os critérios de decisão sobre quais pontos são outliers dependem do modelo que se quer tratar.

No pandas podemos encontrar valores que estão acima ou abaixo de um certo limite.
Lembrando que np.random.randn(M, p) retorna um array de p colunas, cada uma com M valores, retirados aleatoriamente de uma distribuição normal com média 0 e variância 1, começamos por coletar um dataframe para testes.
Considerando os máximos e mínimos exibidos, vamos estabelecer arbitrariamente que valores afastados acima de 3 da média do conjunto são outliers. Isso quer dizer que consideraremos os pontos com |x| > 3 como outliers (onde |x| significa valor absoluto de x). Uma das possibilidades consiste em substituir valores não aceitáveis por np.nan e depois usar uma das formas de fill para preencher esses campos.
» dados = pd.DataFrame(np.random.randn(1000, 4)) » # são os valores mínimo e máximo desse dataframe » dados.min().min(), dados.max().max() ↳ (-3.7113843289590496, 3.480659301328407) » # substituimos |x| > 3 por np.nan » dados[np.abs(dados) > 3] = np.nan » dados.describe() # (1) visualização do dataframe (alguns campos exibidos) ↳ 0 1 2 3 count 996.000000 997.000000 998.000000 996.000000 mean 0.086548 0.021479 -0.046291 0.019611 min -2.772219 -2.860741 -2.763174 -2.644022 max 2.763864 2.849207 2.955914 2.905516 » dados = dados.fillna(method='bfill') » dados.describe() # (2) visualização do dataframe (alguns campos exibidos) ↳ 0 1 2 3 count 1000.000000 1000.000000 1000.000000 1000.000000 mean 0.089292 0.021845 -0.046568 0.020410 min -2.772219 -2.860741 -2.763174 -2.644022 max 2.763864 2.849207 2.955914 2.905516
No primeiro uso de describe a contagem count mostra que existem linhas com campos nulos para cada coluna. Após a operação de fill todos os campos são numéricos.
Removendo linhas duplicadas

Para remover linhas duplicadas em um dataframe usamos df.drop_duplicates(). Valores duplicados em apenas uma coluna podem ser removidos com df.drop_duplicates('nomeColuna'), ou em várias colunas, passando-se uma lista df.drop_duplicates(['col1',..., 'coln']). Por default a primeira linhas, entre as duplicadas é mantida. Para manter a última usamos df.drop_duplicates('coluna', keep='last').
» # remoção de linhas duplicadas
» dic ={'col1': ['vaca', 'vaca', 'pato','pato'], 'col2': [1, 3, 4, 4]}
» df = pd.dfFrame(dic)
» df
↳ col1 col2
0 vaca 1
1 vaca 3
2 pato 4
3 pato 4
» df.duplicated() # retorna uma Series mostrando linhas duplicadas
↳ 0 False
1 False
2 False
3 True
» df.drop_duplicates()
↳ col1 col2
0 vaca 1
1 vaca 3
2 pato 4
» df.drop_duplicates('col1')
↳ col1 col2
0 vaca 1
2 pato 4
» df.drop_duplicates('col1', keep='last')
↳ col1 col2
1 vaca 3
3 pato 4
No atual estado de Pandas não é possível fazer a remoção de duplicadas sobre colunas. Para isso obtenha a transposta do dataframe, remova linhas duplicadas e o transponha novamente.
Transformações sobre elementos de um dataframe
Um restaurante faz uma lista de aquisição de produtos, descrevendo o ítem e quantas unidades devem se adquiridas.
» compra = {'produto':['leite', 'manteiga', 'laranja', 'arroz'],
'quantos':[15, 40,50, 30]}
» dfComprar = pd.DataFrame(compra)
» dfComprar
↳ produto quantos
0 leite 15
1 manteiga 40
2 laranja 50
3 arroz 30
Mais tarde o gerente pede que os produtos sejam classificados como veganos ou não. Para isso podemos usar o método Series.map(dict) que transforma cada elemento usando-o como chave e retornando o valor no dicionário. Construímos um mapeamento entre produto e S/N, conforme o produto seja ou não vegano.
» veg = {'leite':'N', 'manteiga':'N', 'laranja':'S', 'arroz':'S'}
» # dfComprar['produto'] é uma Series e
» dfComprar['produto'].map(lambda x: vegano[x])
↳ 0 N
1 N
2 S
3 S
» # inserindo esse serie em uma nova coluna do df
» dfComprar['vegano'] = dfComprar['produto'].map(veg)
» dfComprar
↳ produto quantos vegano
0 leite 15 N
1 manteiga 40 N
2 laranja 50 S
3 arroz 30 S
» # o mesmo resultado seria obtido com a função lambda
» dfComprar['vegano']=dfComprar['produto'].map(lambda x: vegano[x])
Compartimentação e discretização

Compartimentação e discretização, (Binning e Discretization ) é o processo de particionamento de dados em faixas especificadas. Os compartimentos (faixas ou bins) são representados por variáveis categóricas, que são variáveis que podem assumir apenas um número discreto e limitado de valores, geralmente fixo. Elas estão associadas à propriedades qualitivas do sistema que se observa e podem satisfazer ou não algum critério de ordenamento.
Por ex., suponha que temos um estudo de qualquer natureza centrada sobre indivíduos onde o sexo e a faixa etária são relevantes para as conclusões que se procura obter. O sexo dos indivíduos (digamos que divididos em F = feminino, M = masculino, O = outros) não pode ser ordenado. Mas as faixas etárias são ordenáveis. Dividimos a população estudada em faixas ou bins. Sabendo que todos os participantes são maiores de idade e nenhum tem mais de 98 anos de idade usamos as faixas separadas pelas idades: 18, 34, 50, 66, 82, 98 anos.
» faixas = [18, 34, 50, 66, 82, 98] # definição dos intervalos de idade
» idades = [25, 18, 59, 39, 68, 26, 73, 63, 56, 84] # idade dos indivíduos no estudo
» categorias = pd.cut(idades, faixas)
» categorias
↳ [(18.0, 34.0], NaN, (50.0, 66.0], (34.0, 50.0], (66.0, 82.0], (18.0, 34.0],
(66.0, 82.0], (50.0, 66.0], (50.0, 66.0], (82.0, 98.0]]
Categories (5, interval[int64]): [(18, 34] < (34, 50] < (50, 66] < (66, 82] < (82, 98]]
» # o objeto categorias é do tipo Categorical
» type(categorias)
↳ pandas.core.arrays.categorical.Categorical
» categorias.categories
↳ IntervalIndex([(18, 34], (34, 50], (50, 66], (66, 82], (82, 98]],
closed='right', dtype='interval[int64]')
# O método pd.value_counts(categorias) fornece uma contagem para cada valor existente:
» pd.value_counts(categorias)
↳ (50, 66] 3
(18, 34] 2
(66, 82] 2
(34, 50] 1
(82, 98] 1
» # as colunas são formadas por
» pd.value_counts(categorias).index[0], pd.value_counts(categorias)[0]
↳ (Interval(50, 66, closed='right'), 3)
» nomes_faixas = ['garoto','adulto','semi-novo','vô','matusa']
» categorias = pd.cut(idades, faixas, labels=nomes_faixas)
» categorias
↳ ['garoto', NaN, 'semi-novo', 'adulto', 'vô', 'garoto', 'vô', 'semi-novo', 'semi-novo', 'matusa']
Categories (5, object): ['garoto' < 'adulto' < 'semi-novo' < 'vô' < 'matusa']
» pd.value_counts(categorias)
↳ semi-novo 3
garoto 2
vô 2
adulto 1
matusa 1
» # podemos transformar esse objeto em um dataframe
» dfCont = pd.DataFrame(pd.value_counts(categorias))
» # reordenar índices
» dfConf = dfCont.reindex(['garoto', 'adulto', 'semi-novo', 'vô', 'matusa'])
» dfConf
↳ 0
garoto 2
adulto 1
semi-novo 3
vô 2
matusa 1
As faixas numéricas são estabelecidas em intervalos do tipo (a, b] < (b, c] … representando intervalos abertos no limite inferior e fechados no superior. Isso significa que a não está no primeiro intervalo, mas b está. Para alterar esse comportamento usamos o parâmetro pandas.cut(...,right=False).
Podemos informar em quantas faixas queremos dividir os dados, ao invés de passar explicitamente essas faixas. Nesse caso o método pandas.cut(dados, n, precision=p) calculará n intervalos iguais baseados nos valores máximos e mínimos dos dados. precision=p determina a precisão decimal das faixas.
» # array com 20 numeros aleatórios » dados = np.random.rand(20)*10 » dados.min(), dados.max() # valores mínimo e máximo ↳ (1.0012658194039414, 9.799331139583924) » # 3 faixas (bins) » picado = pd.cut(dados, 3, precision=2) » pd.value_counts(picado) ↳ (6.87, 9.8] 10 (0.99, 3.93] 7 (3.93, 6.87] 3
Para distribuir dados em faixas baseadas em quantis usamos o método pandas.qcut(dados, n), onde n é o número de partes na partição. Intervalos de quantis customizados podem ser conseguidos passando-se uma lista em pandas.qcut(dados, lista).
» data = np.random.randn(1000) # 1000 números aleatórios » categorias = pd.qcut(data, 4) # distribui em quartis » pd.value_counts(categorias) ↳ (-3.0309999999999997, -0.683] 250 (-0.683, 0.0106] 250 (0.0106, 0.702] 250 (0.702, 3.196] 250 » # intervalos de quantis customizados » pd.value_counts(pd.qcut(data, [0, 0.1, 0.5, 0.9, 1.])) ↳ (-1.223, 0.0106] 400 (0.0106, 1.301] 400 (-3.0309999999999997, -1.223] 100 (1.301, 3.196] 100
Permutações aleatórias

Permutações entre as linhas (ou colunas) de um dataframe são obtidas com dataframe.take(arr), onde arr é um array com a ordem dos índices desejada. Se essa ordem for “sorteada” o dataframe fica com linhas em ordem “aleatoria”. Para reordenar colunas usamos axis=1. dataframe.sample(n) seleciona n linhas do dataframe, sem repetições (n < dataframe.shape[0]) e dataframe.sample(n, replace=True) retorna n linhas do dataframe que podem ser repetidas (como em um sorteio com reposição dos elementos sorteados).
» # dataframe de teste » df = pd.DataFrame(np.arange(16).reshape((4, 4))) » df ↳ 0 1 2 3 0 0 1 2 3 1 4 5 6 7 2 8 9 10 11 3 12 13 14 15 » sorteio = np.random.permutation(4) # permutação aleatória de 0, 1, 2 e 3 » sorteio ↳ array([3, 2, 0, 1]) » df.take(sorteio) # dataframe na ordem de linhas sorteadas ↳ 0 1 2 3 3 12 13 14 15 2 8 9 10 11 0 0 1 2 3 1 4 5 6 7 » df.take(sorteio, axis=1) # dataframe na ordem de colunas sorteadas ↳ 3 2 0 1 0 3 2 0 1 1 7 6 4 5 2 11 10 8 9 3 15 14 12 13 » df.sample(n=2) # 2 linhas selecionadas aleatoriamente ↳ 0 1 2 3 1 4 5 6 7 3 12 13 14 15 » df.sample(n=2, axis=1) # 2 colunas selecionadas aleatoriamente ↳ 3 1 0 3 1 1 7 5 2 11 9 3 15 13 » df.sample(n=4, replace=True) # 4 linhas selecionadas aleatoriamente, com reposição ↳ 0 1 2 3 0 0 1 2 3 0 0 1 2 3 1 4 5 6 7 0 0 1 2 3
O mesmo dataframe obtido com df.take(sorteio) poderia ser conseguido com df.iloc[sorteio].
Indicador de computação, variáveis fictícias
Na estatística, econometria e aprendizado de máquina uma variável fictícia (variável dummy ) é uma representação de um efeito categórigo assumindo apenas os valores 0 ou 1 para indicar presença ou ausência de alguma forma de caracterização. Elas podem ser consideradas como representações numéricas de aspectos qualitativos. Um exemplo simples seria a representação da classificação de uma conta bancária como poupança (0) ou conta corrente (1).
Uma variável categórica pode ser transformada em uma matriz dummy ou de indicadores. Se uma series (uma coluna de um dataframe) possui p valores distintos podemos obter um dataframe com o mesmo número de colunas, cada uma contendo apenas 0 ou 1. Para isso usamos o método pandas.get_dummies(Series) que retorna um dataframe marcando as posições onde cada um dos p valores ocorrem. Um prefixo pode ser acrescentado aos nomes das colunas com pandas.get_dummies(Series, prefix='p').
Por ex., em uma pesquisa foi marcado, para cada indivíduo participante, o campo sexo = F (feminino), M (masculino), O (outros).
» df = pd.DataFrame({'individuo': ['Fulano', 'Beltrano', 'Cicrano', 'Deltrano', 'Cruciano', 'Marciano'],
'sexo': ['H','H','H','F','O','F']})
» df
↳ individuo sexo
0 Fulano H
1 Beltrano H
2 Cicrano H
3 Deltrano F
4 Cruciano O
5 Marciano F
» # categorizando a coluna 'sexo'
» pd.get_dummies(df['sexo'])
↳ F H O
0 0 1 0
1 0 1 0
2 0 1 0
3 1 0 0
4 0 0 1
5 1 0 0
» # inserindo um prefixo (no nome das colunas)
» pd.get_dummies(df['sexo'], prefix='sexo').head(2)
↳ sexo_F sexo_H sexo_O
0 0 1 0
1 0 1 0
Muitas vezes os dados devem ser manipulados e preparados para uma devida categorização. Suponha que temos uma lista de autores, cada um associado a um ou mais gêneros literários separados por |. Queremos uma listagem de autores versus gêneros, marcando em qual gênero cada um escreve.
» # importamos de qualquer fonte o seguinte dataframe: » dfAutores ↳ autor genero 0 Antonio poesia|conto 1 José romance 2 Marco ficção|biografia 3 Pedro poesia|conto » # cada autor está associado a um ou mais gêneros » genero = dfAutores.genero » autores = dfAutores.autor » # as duas séries têm o mesmo comprimento (len(autores) = len(generos) = 4, 4
Criamos uma lista vazia e a preenchemos com todos os gêneros, quebrando os campos em |. Depois usamos pandas.unique(lista) para conseguir um array com os gêneros, sem repetições, como em um conjunto (set).
» lista = []
» for t in genero:
» lista.extend(t.split('|'))
» unicos = pd.unique(lista)
» unicos
↳ array(['poesia', 'conto', 'romance', 'ficção', 'biografia'], dtype=object)
Em seguida criamos um dataframe de zeros com os autores nas colunas e gêneros nas linhas.
» dfZero = pd.DataFrame(np.zeros((len(unicos),len(autores))), index=unicos, columns=autores).astype(int)
» dfZero # estado inicial de dfZero
↳ autor Antonio José Marco Pedro
poesia 0 0 0 0
conto 0 0 0 0
romance 0 0 0 0
ficção 0 0 0 0
biografia 0 0 0 0
# preenchemos esse dataframe
» for i in range(len(unicos)):
» for k in range(len(genero)):
» if unicos[i] in genero[k]:
» dfZero.iloc[i,k] = 1
» dfZero # estado final de dfZero
↳ autor Antonio José Marco Pedro
poesia 1 0 0 1
conto 1 0 0 1
romance 0 1 0 0
ficção 0 0 1 0
biografia 0 0 1 0
O duplo loop sobre a lista de gêneros únicos, unicos, e a lista original de gêneros genero faz a verificação se um dos generos está em genero1|genero2…. Por exemplo, na linha 3, coluna 2 temos:
» unicos[3], genero[2], unicos[3] in genero[2]
↳ ('ficção', 'ficção|biografia', True)
Se o resultado é verdadeiro o dataframe terá o campo correspondente trocado para 1. Os demais permanecem com o valor 0. O dataframe final é o resultado desejado.
Tratamento de campos de texto
Operações com strings são também vetorializadas no pandas. No ex. usamos os códigos telefones dos países: 55-Brasil, 47-Noruega, 52-México. Construímos duas séries e as concatenamos em um dataframe, df = pd.concat([serie, srPais], axis=1).
» lista = ['055-11-12345678', '047-21-87654321', '055-11-13579135', '052-78-45665412']
» serie = pd.Series(lista)
» serie
↳ 0 055-11-12345678
1 047-21-87654321
2 055-11-13579135
3 052-78-45665412
» # booleano, linhas que contém '-11-'
» serie.str.contains('-11-')
↳ 0 True
1 False
2 True
3 False
» # linhas que contém '-11-'
» serie[serie.str.contains('-11-')]
↳ 0 055-11-12345678
2 055-11-13579135
» # lista com os códigos dos países
» codigos = [x.split('-')[0] for x in lista]
» codigos
↳ ['055', '047', '055', '052']
» # dicionário para conversão código ⇒ país
» pais = {'055':'Brasil', '047':'Noruega', '052':'México'}
» srPais = pd.Series([pais[x] for x in codigos]) # veja comentário †
» srPais
↳ 0 Brasil
1 Noruega
2 Brasil
3 México
» # juntamos as duas series em um dataframe
» df = pd.concat([serie, srPais], axis=1)
» df = df.rename(columns = {0:'telefone', 1:'pais'})
» df
↳ telefone pais
0 055-11-12345678 Brasil
1 047-21-87654321 Noruega
2 055-11-13579135 Brasil
3 052-78-45665412 México
» # nome do país começado com 'No'
» df[df['pais'].str.startswith('No')]
↳ telefone pais
1 047-21-87654321 Noruega
» # acrescenta campo com 3 primeiras letras do nome
» df['abreviado'] = df['pais'].str[:3]
» df
↳ telefone pais abreviado
0 055-11-12345678 Brasil Bra
1 047-21-87654321 Noruega Nor
2 055-11-13579135 Brasil Bra
3 052-78-45665412 México Méx
(†): A linha srPais = pd.Series([pais[x] for x in codigos]) (uma compreensão de lista) percorre os valores em codigos e os usa como chaves no dicionário pais, retornando seus valores.
Bibliografia
- McKinney, Wes: Python for Data Analysis, Data Wrangling with Pandas, NumPy,and IPython
O’Reilly Media, 2018.
Consulte bibliografia completa em Pandas, Introdução neste site.
Nesse site:







 No caso de arrays bidimensionais os elementos do array são acessados pelos índices de suas linhas e colunas, sendo que
No caso de arrays bidimensionais os elementos do array são acessados pelos índices de suas linhas e colunas, sendo que