Vimos que uma base de um espaço vetorial \(V\) é um conjunto de vetores de \(V\) que são linearmente independentes que geram este espaço vetorial. Vimos ainda que, escolhida uma base \(\alpha = \{v_1, v_2, \ldots, v_n \}\) então todo vetor de \(V\) pode ser escrito de forma única como combinação linear dos vetores desta base, \(v = a_1 v_1 + a_2 v_2 + \ldots + a_n v_n\).

Em muitas situações pode ser interessante descrever um vetor, ou outro objeto formado por vetores, em mais de uma base, lembrando que, alterada a base alteram-se também os coeficientes do vetor naquela base. é possível, em muitos casos, que a descrição se torne muito simplificada com a escolha mais adequada da base a ser usada. Um exemplo ilustrará a importância desta operação de mudança de bases.

Exemplo: A relação \(x^2 + x y + y^2 – 3 = 0\) descreve uma elipse no plano, como está ilustrado na figura 1.

Em um novo sistema de coordenadas \((x’, y’)\) obtido por rotação dos eixos de coordenadas de um ângulo de \(45^0\) antihorário. Por meio de uma mudança adequada de base, que pode ser vista como a introdução de um novo sistema de coordenadas, a mesma elipse fica expressa como \(3 x^{\prime 2} + 2 y^{\prime 2}\) =6, onde os sistemas \((x, y)\) e \((x’, y’)\) se relacionam de uma forma que ficará clara em breve.

Considere que em um dado espaço vetorial \(V\) temos duas bases, \(\beta = \{u_1, \ldots, u_n \}\) e \(\beta’ = \{w_1, \ldots, w_n \}\). Então, se \(v\) é um vetor deste espaço, podemos escrevê-lo nas duas bases, respectivamente como
$$ v = x_1 u_1 + \ldots + x_n u_n, $$
$$ v = y_1 w_1 + \ldots + y_n w_n. $$

Queremos relacionar os dois grupos de coordenadas
$$
[v]_{\beta} = \left[ \begin{array}{r}
x_1\\
\ldots\\
x_n
\end{array} \right], [v]_{\beta’} = \left[ \begin{array}{r}
y_1\\
\ldots\\
y_n
\end{array} \right] .
$$

é importante observar que \(v\) é um objeto geométrico, independente do sistema de coordenadas usado ou, o que é equivalente, independente da base usada para este espaço vetorial. A transformação pode ser conseguida da seguinte forma: cada um dos vetores da base \(\beta’\) pode ser escrito como combinação dos vetores da base \(\beta\), uma vez que também são vetores de \(V\), portanto
$$
\begin{array}{lr}
w_1 = & a_{11} u_1 + \ldots + a_{n 1} u_n,\\
w_2 = & a_{12} u_1 + \ldots + a_{n 2} u_n,\\
\vdots & \vdots\\
w_n = & a_{1 n} u_1 + \ldots + a_{n n} u_n .
\end{array}
$$

A escolha de índices das constantes \(a_{i j}\) acima ficará clara a seguir. Substituindo os vetores acima em \(v = y_1 w_1 + \ldots + y_n w_n\) temos
$$
\begin{array}{rll}
v = & y_1 (a_{11} u_1 + \ldots + a_{n 1} u_n) + & \ldots & + y_n (a_{1n} u_1 + \ldots + a_{n n} u_n) = \\
& (a_{11} y_1 + \ldots + a_{1 n} y_n) u_1 + & \ldots & + (a_{n 1} y_1+ \ldots + a_{n n} y_n) u_n .
\end{array}
$$

Na última linha foram colocados em evidência os vetores \(u_k\). Como podemos escrever \(v = x_1 u_1 + \ldots + x_n u_n\) (usando a base \(\beta\) ) e, lembrando que existe uma única combinação linear para descrever um vetor em cada base, podemos identificar os termos
$$ \begin{array}{r}
x_1 = a_{11} y_1 + \ldots + a_{1 n} y_n, \\
\vdots \\
x_n = a_{n 1} y_1 + \ldots + a_{n n} y_n,
\end{array} $$
que é exatamente a regra de transformação entre as coordenadas \(\{y_k \}\) na base \(\beta’\) para as coordenadas \(\{x_k \}\) na base \(\beta\). Podemos escrever a mesma expressão acima em forma matricial como
$$
\left[ \begin{array}{r}
x_1\\
\vdots\\
x_n
\end{array} \right] = \left[ \begin{array}{lll}
a_{11} & \ldots & a_{1 n}\\
\vdots & & \vdots\\
a_{n 1} & \ldots & a_{n n}
\end{array} \right] \left[ \begin{array}{r}
y_1\\
\vdots\\
y_n
\end{array} \right],
$$
onde se observa que a escolha dos índices, citada acima, leva a uma disposição natural dos elementos formadores da matriz de transformação. Denotaremos por
$$
I^{\beta’}_{\beta} = \left[ \begin{array}{rrr}
a_{11} & \ldots & a_{1 n}\\
\vdots & & \vdots\\
a_{n 1} & \ldots & a_{n \, n}
\end{array} \right]
$$

esta matriz, a chamada matriz mudança de base de \(\beta’\) para \(\beta\), onde os coeficientes \(a_{i j}\) são as coordenadas dos vetores \(w_k\) (os elementos do base \(\beta’\) ) na base \(\beta\). Com esta notação a transformação entre uma base e outra fica descrita por
$$ [v]_{\beta} = I^{\beta’}_{\beta} [v]_{\beta’}, $$
lembrando que os coeficientes de \(I^{\beta’}_{\beta} = \{a_{i j} \} \) são as coordenadas dos vetores da base \(\beta’\) \((w_j)\) desenvolvidos na base \(\beta = \{u_j \}\).

Repetindo de forma compacta: Considere que em um dado espaço vetorial \(V\) temos duas bases, \(\beta = \{u_i \}\) e \(\beta’ = \{w_j \}\). Se \(v \in V\), podemos escrevê-lo nas duas bases, como
$$ v = \sum_{i = 1}^n x_i u_i, \;\; \text{e} \;\; v = \sum_{j = 1}^n y_j w_j.$$
Queremos relacionar os dois conjuntos de coordenadas \(\{x_i \}\) e \(\{y_j \}\). Lembrando que cada um dos \(w_j \in V\) temos que
$$ w_i = \sum_{k = 1}^n a_{k i} u_k, i = 1, \ldots, n.$$
Substituindo na expressão para \(v\)
$$ v = \sum_{i = 1}^n y_i w_i = \sum_{i = 1}^n y_i \left( \sum_{k = 1}^n a_{k i} u_k \right) = $$
$$ = \sum_{k = 1}^n \left( \sum_{i = 1}^n a_{k i} y_i \right) u_k = \sum_{k = 1}^n x_k u_k.$$
Como os dois termos na expressão acima correspondem à decomposição do vetor \(v\) na base \(\beta\), e esta decomposição é única, podemos identificar
$$ x_k = \sum_{i = 1}^n a_{k i} y_i $$
ou seja
$$ [v]_{\beta} = I^{\beta’}_{\beta} [v]_{\beta’}, $$
onde os coeficientes de \(I^{\beta’}_{\beta} = \{a_{i j} \} \) são as coordenadas dos vetores da base \(\beta’\) \((w_j)\) desenvolvidos na base \(\beta
= \{u_j \}\).

Exemplo: Dadas duas bases de \(\mathbb{R}^2,\;\; \beta = \{(2, – 1), (3, 4)\}\) e \(\beta’ = \{(1, 0) (0, 1)\}\) procuramos a matriz \(I_{\beta}^{\beta’}\), a matriz de mudança de base de \(\beta’\) para \(\beta\). Primeiro encontramos a decomposição dos vetores de \(\beta’\) na base \(\beta\) (dos vetores da base de partida descritos na base de chegada):
$$
(1, 0) = a_{11} (2, – 1) + a_{21} (0, 1),
$$

$$
(0, 1) = a_{12} (2, – 1) + a_{22} (0, 1),
$$

o que nos leva a dois sistemas, e suas respectivas soluções
$$
\left\{ \begin{array}{r}
2 a_{11} + 3 a_{21} = 1\\
– a_{11} + 4 a_{21} = 0
\end{array} \Rightarrow \left\{ \begin{array}{r}
a_{11} = 4 / 11,\\
a_{21} = 1 / 11,
\end{array} \right. \right.
$$

$$
\left\{ \begin{array}{r}
2 a_{12} + 3 a_{22} = 0\\
– a_{12} + 4 a_{22} = 1
\end{array} \Rightarrow \left\{ \begin{array}{r}
a_{12} = – 3 / 11,\\
a_{22} = 2 / 11.
\end{array} \right. \right.
$$

Portanto, a matriz mudança de base de \(\beta’\) para \(\beta\) é
$$
I_{\beta}^{\beta’} = \left[ \begin{array}{rr}
4 / 11 & – 3 / 11\\
1 / 11 & 2 / 11
\end{array} \right] = \frac{1}{11} \left[ \begin{array}{rr}
4 & – 3\\
1 & 2
\end{array} \right] .
$$

Vamos prosseguir um pouco mais com este mesmo exemplo para compreender como se dá esta mudança de base. Dado o vetor \(v = (5, – 8)\) ele pode ser imediatamente escrito na base \(\beta’\) (que é a base canônica) como
$$
[v]_{\beta’} = \left[ \begin{array}{r}
5\\
– 8
\end{array} \right] .
$$

As coordenadas deste vetor na base \(\beta’\) são
$$
[v]_{\beta} = \frac{1}{11} \left[ \begin{array}{rr}
4 & – 3\\
1 & 2
\end{array} \right] \left[ \begin{array}{r}
5\\
– 8
\end{array} \right] = \left[ \begin{array}{r}
4\\
– 1
\end{array} \right] .
$$
Podemos verificar diretamente que isto está correto pois \((5, – 8) = 4 (2, – 1) – 1 (3, 4)\).

Além de converter um vetor de uma base para outra, é interessante conhecer um procedimento para obter a operação inversa, ou seja, retornar da base nova para a base antiga. Isto nos leva a considerar a inversa da matriz mudança de base.

Vimos que a mudança de base de \(\beta’\) para \(\beta\) pode ser realizada por meio da operação
$$
[v]_{\beta} = I^{\beta’}_{\beta} [v]_{\beta’} .
$$

Denotamos por \( [I^{\beta’}_{\beta}]^{- 1}\) a inversa da matriz acima, e multiplicando à esquerda temos
$$ [I^{\beta’}_{\beta}]^{- 1} [v]_{\beta} = [I^{\beta’}_{\beta}]^{- 1} I^{\beta’}_{\beta} [v]_{\beta’} = [v]_{\beta’}. $$
Isto significa que
$$ [v]_{\beta’} = I^{\beta}_{\beta’} [v]_{\beta} = [I^{\beta’}_{\beta}]^{- 1} [v]_{\beta}, $$
ou seja, a matriz \(I_{\beta’}^{\beta}\) (a mudança de base de \(\beta\) para \( \beta’\) ) é a inversa de \(I_{\beta}^{\beta’}\),
$$ I^{\beta}_{\beta’} = [I^{\beta’}_{\beta}]^{- 1}. $$

Exemplo: No exemplo anterior, vamos procurar a matriz mudança de base de \(\beta\) para \(\beta’\), onde \(\beta = \{(2, – 1), (3, 4)\}\) e \(\beta’ = \{(1, 0) (0, 1)\}\). Os vetores de \(\beta\) na base \(\beta’\) tem coordenadas
$$ (2, – 1) = 2 (1, 0) – 1 (0, 1), $$
$$ (3, 4) = 3 (1, 0) + 4 (0, 1), $$

e, portanto
$$
I_{\beta’}^{\beta} = \left[ \begin{array}{rr}
2 & 3\\
– 1 & 4
\end{array} \right]
$$

Podemos verificar que esta é, de fato, a inversa de \(I_{\beta}^{\beta’}\) obtida acima, pois
$$
I_{\beta’}^{\beta} I_{\beta}^{\beta’} = \frac{1}{11} \left[
\begin{array}{rr}
2 & 3\\
– 1 & 4
\end{array} \right] \left[ \begin{array}{rr}
4 & – 3\\
1 & 2
\end{array} \right] = \left[ \begin{array}{rr}
1 & 0\\
0 & 1
\end{array} \right] .
$$

Exemplo: Uma mudança de base importante está associada a uma rotação dos eixos de coordenadas. Em \(\mathbb{R}^2\) considere que \(\beta = (\hat{e}_1, \hat{e}_2)\) é a base canônica e \(\beta’ = (\hat{f}_1, \hat{f}_2)\) a base obtida de \(\beta\) por meio de uma rotação antihorária de um ângulo \(\theta\), como indicado na figura 2.

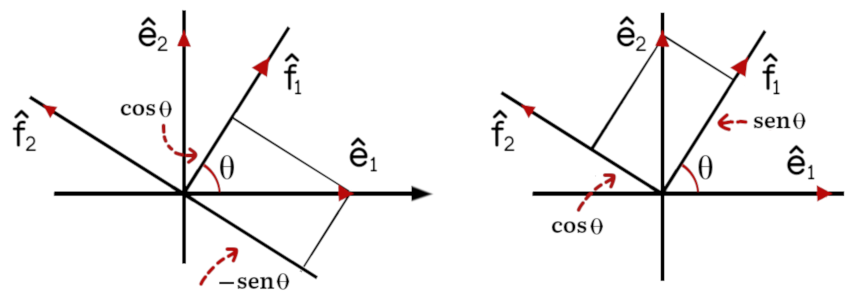
Analisando a figura podemos ver que
$$ \hat{e}_1 = \cos \theta \hat{f}_1 – \text{sen } \theta \hat{f}_2, $$

$$ \hat{e}_2 = \text{sen } \theta \hat{f}_1 + \cos \theta \hat{f}_2, $$

e, portanto, temos a matriz mudança de base,
$$
I_{\beta’}^{\beta} = \left[ \begin{array}{rr}
\cos \theta & \text{sen } \theta\\
– \text{sen } \theta & \cos \theta
\end{array} \right] .
$$

Se descrevermos um vetor (pode ser, por exemplo, uma posição) com relação ao sistema de eixos originais por meio de suas coordenadas usuais \((x, y)\) podemos obter as coordenadas \((x’, y’)\) no sistema após a rotação como
$$
\left[ \begin{array}{r}
x’\\
y’
\end{array} \right] = \left[ \begin{array}{rr}
\cos \theta & \text{sen } \theta\\
– \text{sen } \theta & \cos \theta
\end{array} \right] \left[ \begin{array}{r}
x\\
y
\end{array} \right] .
$$

Como um caso particular, se \(\theta = \pi / 3\) temos \(\text{sen } (\pi / 3) =\sqrt{3} / 2\) e \(\cos (\pi / 3) = 1 / 2\) e
$$
I_{\beta’}^{\beta} = \frac{1}{2} \left[ \begin{array}{rr}
1 & \sqrt{3}\\
– \sqrt{3} & 1
\end{array} \right] .
$$

Um vetor \(\vec{v} = (- 2, 3)\) tem coordenadas
$$
[\vec{v}]_{\beta’} = \frac{1}{2} \left[ \begin{array}{rr}
1 & \sqrt{3}\\
– \sqrt{3} & 1
\end{array} \right] \left[ \begin{array}{r}
– 2\\
3
\end{array} \right] = \frac{1}{2} \left[ \begin{array}{r}
– 2 + 3 \sqrt{3}\\
2 \sqrt{3} + 3
\end{array} \right],
$$

ou seja,
$$
\vec{v} = \left( \frac{- 2 + 3 \sqrt{3}}{2} \right) \widehat{f_1} + \left(
\frac{2 \sqrt{3} + 3}{2} \right) \widehat{f_2} .
$$

Por outro lado, escrevendo os vetores de \(\beta’\) na base \(\beta\) temos
$$
\hat{f}_1 = \cos \theta \hat{e}_1 + \text{sen } \theta \hat{e}_2,
$$

$$
\hat{f}_2 = – \text{sen } \theta \hat{e}_1 + \cos \theta \hat{e}_2,
$$

e a matriz mudança de base \(\beta’ \rightarrow \beta\) é
$$
I_{\beta}^{\beta’} = \left[ \begin{array}{rr}
\cos \theta & – \text{sen } \theta\\
\text{sen } \theta & \cos \theta
\end{array} \right],
$$

que consiste na matriz de rotação de um ângulo de \(– \theta\) (ou \(\theta\), no sentido horário). Se fizermos uma rotação de um ângulo \(\theta\), seguida de uma rotação de ângulo \(– \theta\), voltaremos à posição original, equivalente a fazer uma rotação de ângulo nulo ou deixar inalterado o vetor a ser girado,
$$
\left[ \begin{array}{rr}
\cos \theta & – \text{sen } \theta \\
\text{sen } \theta & \cos \theta
\end{array} \right]
\left[ \begin{array}{rr}
\cos \theta & \text{sen } \theta\\
– \text{sen } \theta & \cos \theta
\end{array}\right] = \left[ \begin{array}{rr}
1 & 0\\
0 & 1
\end{array} \right].
$$