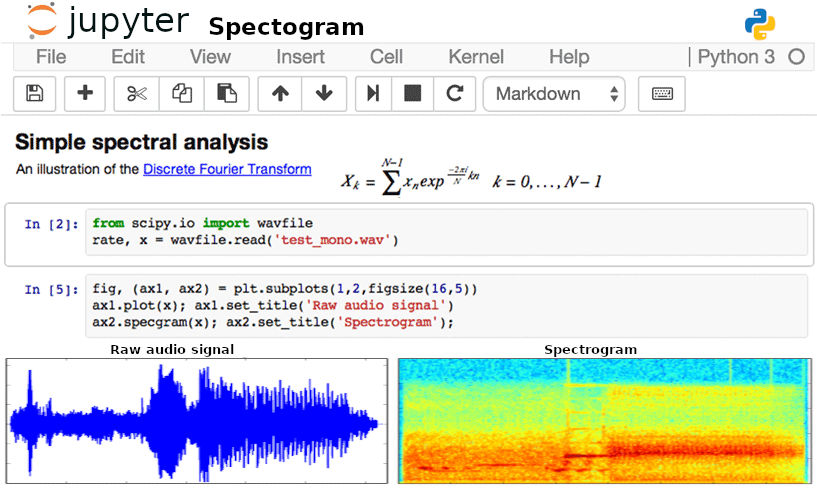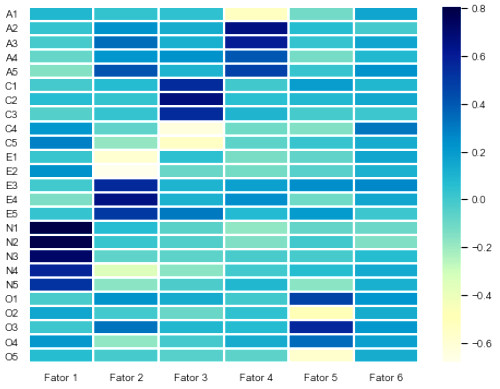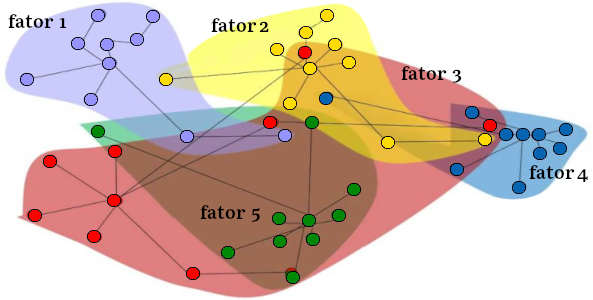
FactorAnalyzer é um módulo Python para realizar análise fatorial exploratórias (AFE) e confirmatória (AFC). Na análise exploratória se pode usar várias técnicas de estimativa. É possível executar AFE usando (1) solução residual mínima (MINRES), (2) uma solução de máxima verossimilhança ou (3) uma solução de fator principal. A análise confirmatória só pode ser executada usando uma solução de máxima verossimilhança.
As classes da biblioteca são compatíveis com scikit-learn. Partes do código são portadas da biblioteca psych do R, e a classe AFC foi baseada na biblioteca sem. A classe factor_analyzer.factor_analyzer.FactorAnalyzer se utiliza de sklearn.base.BaseEstimator e sklearn.base.TransformerMixin.
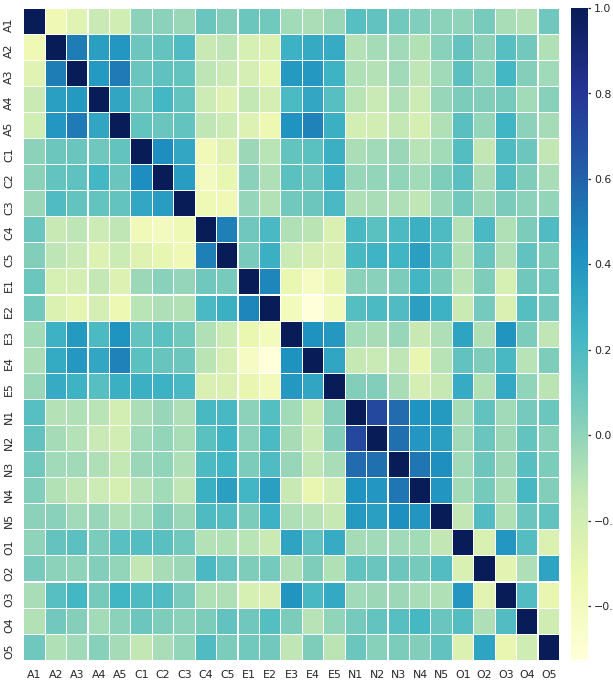
Na AFE as matrizes de carga fatorial são geralmente submetidas a rotações após o modelo de análise fatorial ser estimado, buscando-se produzir uma estrutura mais simples e de fácil interpretação na identificação das variáveis que estão carregando em um determinado fator.
Os dois tipos mais comuns de rotações são:
- Rotação ortogonal varimax, que gira a matriz de cargas fatoriais de forma a maximizar a soma da variância das cargas quadradas, preservando a ortogonalidade da matriz de carga.
- A rotação oblíqua promax, baseada na rotação varimax, mas buscando maior correlaçãp dos fatores.
Essa biblioteca inclui o módulo analisador de fatores com a classe FactorAnalyzer. Essa classe inclui os métodos fit() e transform() para realizar a análise e pontuar novos dados usando o modelo de fatores ajustados. Rotações opcionais podem ser realizadas sobre a matriz de cargas fatoriais com a classe Rotator.
Os seguintes métodos de rotação estão disponíveis tanto para FactorAnalyzer quanto para Rotator:
- varimax (rotação ortogonal),
- promax (oblíqua),
- oblimin (oblíqua),
- oblimax (ortogonal),
- quartimin (oblíqua),
- quartimax (ortogonal),
- equamax (ortogonal),
- geomin_obl (oblíqua),
- geomin_ort (ortogonal).
A biblioteca também inclui o módulo confirmatory_factor_analyzer com a classe ConfirmatoryFactorAnalyzer. A classe contém os métodos fit() e transform() que realizam análises fatoriais confirmatórias e pontuam novos dados usando o modelo ajustado. A execução do CFA requer que os usuários especifiquem previamente o modelo com as relações de carga fatorial esperadas, o que pode ser feito usando a classe ModelSpecificationParser.
# A biblioteca pode ser instalada usando pip: $ pip install factor_analyzer # ou conda: $ conda install -c ets factor_analyzer
Ele depende de Python 3.4 (ou superior), numpy, pandas, scipy, scikit-learn.
A classe factor_analyzer possui um método para ajustar um modelo de análise e fazer a análise fatorial usando solução residual mínima (MINRES), solução de máxima verossimilhança ou (3) solução de fator principal. Retorna a matriz de cargas fatoriais. Por default não realiza nenhuma rotação. Opcionalmente pode realizar uma rotação usando os métodos citados abaixo.
Análise Fatorial Exploratória
Módulo factor_analyzer.factor_analyzer
class
factor_analyzer.factor_analyzer.FactorAnalyzer(n_factors=3, rotation='promax', method='minres',
use_smc=True, is_corr_matrix=False, bounds=(0.005, 1),
impute='median', rotation_kwargs=None)
- n_factors
- (int, opcional) – Número de fatores a ajustar. Default: 3.
- rotation
- (str, opcional) – Default: None.
Define o tipo de rotação a realizar após o ajuste do modelo. Nenhuma rotação será realizada se rotation = None e nenhuma normalização de Kaiser será aplicada. Os seguintes métodos de rotação estão disponíveis:- varimax (rotação ortogonal),
- promax (oblíqua),
- oblimin (oblíqua),
- oblimax (ortogonal),
- quartimin (oblíqua),
- quartimax (ortogonal),
- equamax (ortogonal),
sendo rotation = ‘promax’ o default.
- method
- ({‘minres’, ‘ml’, ‘principal’}, opcional) – Método de ajuste a ser usado: solução residual mínima (MINRES), uma solução de máxima verossimilhança ou de fator principal. Default: minres.
- use_smc
- (bool, opcional) – Uso de correlação multipla quadrada (SMC, square multiple correlation) como ponto de partida para a análise. Default: True.
- bounds
- (tuple, opcional) – Limites inferior e superior das variáveis para a otimização “L-BFGS-B”. Default: (0.005, 1).
- impute
- ({‘drop’, ‘mean’, ‘median’}, opcional) – Se existem valores faltantes nos dados usar apagamento na lista inteira (‘drop’) ou substituir valores usando a mediana (‘median’) ou a média (‘mean’) da coluna.
- use_corr_matrix
- (bool, opcional) – Ajuste para Verdadeiro se os dados de entrada já são a matriz de correlação. Default: False.
- rotation_kwargs
- (opcional) – argumentos adicionais passados para o método de rotação.
- loadings
- A matriz de cargas fatoriais. Default: None se o método
fit()não foi chamado.
Tipo: numpy array - corr
- A matriz original de correlação. Default: None se o método
fit()não foi chamado.
Tipo: numpy array - rotation_matrix
- A matriz de rotação, se uma rotação não foi executada.
Tipo: numpy array - structure
- A estrutura da matriz de cargas fatoriais. (Só existe se rotação for promax).
Tipo: numpy array ou None - psi
- A matriz de fatores de correlação. (Só existe se rotação for oblíqua).
Tipo: numpy array ou None - fit(X, y=None)
- Faz a análise fatorial sobre os dados de X usando ‘minres’, ‘ml’, ou ‘principal solutions’. Default: SMC (correlação múltipla quadrada)
Parâmetros:
X (variável tipo array) – Dados originais a serem analisados.
y (não é utilizado). - get_communalities()
- Calcula as comunalidades, dada uma matriz de cargas fatoriais.
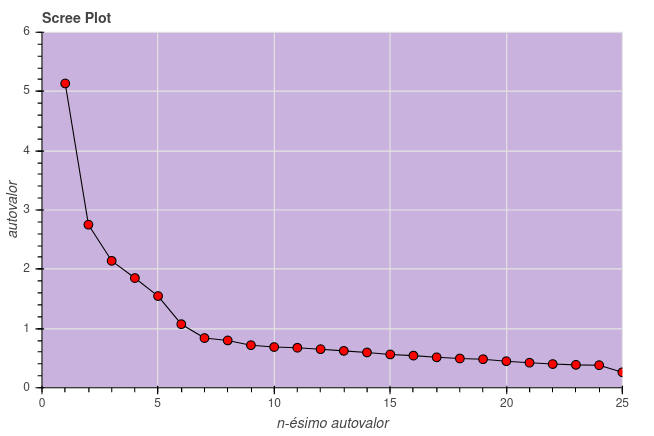
Retorna:communalities(numpy array), as comunalidades. - get_eigenvalues()
- Calcula os autovalores, dada uma matriz de correlações fatoriais.
Retorna:original_eigen_values(numpy array), os autovalores originais.
common_factor_eigen_values(numpy array), os autovalores dos fatores comuns. - get_factor_variance()
- Calcula informações de variância, inclusive a variância, variância proporcional e cumulativa para cada fator.
Retorna:variance(numpy array) – A variância dos fatores.
proportional_variance(numpy array) – A variância proporcional dos fatores.
cumulative_variances(numpy array) – A variância cumulativa dos fatores. - get_uniquenesses()
- Calcula a unicidade, dada uma matriz de cargas fatoriais.
Retorna:uniquenesses(numpy array) – A unicidade da matriz de cargas fatoriais. - transform(X)
- Retorna a pontuação de fatores para um novo conjunto de dados.
Parâmetros: X (variável de array, shape (n_amostras, n_características)) – Os dados a pontuar usando o modelo de fatores ajustado.
Retorna: X_new – As variáveis latentes de X. (um numpy array, shape (n_amostras, n_componentes)) - Parâmetro
- X (variável de array) – Dados sobre os quais calcular a esfericidade.
- Retorna:
- statistic (float) – O valor de chi-quadrado, \chi^2.
p_value (float) – O valor de p-value associado ao teste. - Parâmetros:
- x (variável de array) – Dados sobre os quais calcular coeficientes KMOs.
- Retorna:
- kmo_per_variable (array numpy) – O KMO para cada item.
kmo_total (float) – A pontuação KMO geral. - specification
- (ModelSpecification object ou None, opcional) – Um modelo de especificação ModelSpecification ou None. Se None for fornecido o ModelSpecification será gerado supondo que o número de fatores n_factors é o mesmo que o número de variáveis, n_variables, e que todas as variáveis carregam em todos os fatores. Note que isso pode significa que o modelo não foi identificado e a otimização poderá falhar. Default: None.
- n_obs
- (int ou None, opcional) – Número de observações no conjunto original de dados. Se não for passado e is_cov_matrix=True um erro será lançado. Default: None.
- is_cov_matrix
- (bool, opcional) – Informa se a matriz de entrada X é a matriz de covariância. Se False o conjunto completo de dados é considerado. Default: False.
- bounds
- (lista de tuplas ou None, opcional) – Uma lista de limites mínimos e máximos para cada elemento do array de entrada. Deve ser igual a x0 que é o array de entrada do modelo de especificação.
O comprimento é: ((n_factors * n_variables) + n_variables + n_factors + (((n_factors * n_factors) – n_factors) // 2)
Se bounds=None nenhum limite será tomado. Default: None.
- max_iter
- (int, opcional) – Número máximo de iterações na rotina de otimização. Default: 200.
- tol
- (float ou None, opcional) – Tolerância para a convergência. Default: None.
- disp
- (bool, opcional) – Se a mensagem da otimização do scipy fmin é enviado para o standard output. Default: True.
- Exceção levantada
- ValueError – Se is_cov_matrix = True e n_obs não é fornecido.
- model
- Objeto modelo de especificação.
Tipo: ModelSpecification. - loadings_
- A Matriz da Cargas fatoriais.
Tipo: numpy array - error_vars_
- A matriz de variância de erros (Tipo: numpy array).
- factor_varcovs_
- A Matriz de covariância. (Tipo: numpy array).
- log_likelihood_
- O log de verossimilhança da rotina de otimização. (Tipo: float).
- aic_
- O critério de informação de Akaike. (Tipo: float).
- bic_
- O critério de informação Bayesiano. (Tipo: float).
- fit(X, y=None)
- realiza a análise fatorial confirmatória sobre os dados de X usando máxima verossimilhança.
Parâmetros:
X (variável tipo array) – Dados originais a serem analisados. Se X for a matriz de covariância é necessário marcar is_cov_matrix = True.
y (não é utilizado) - Exceção levantada:
- ValueError – Se a especificação não é um objeto ModelSpecification nem None.
AssertionError – Se is_cov_matrix = True e a matriz fornecida não é quadrada.
AssertionError – If len(bounds) != len(x0) - get_model_implied_cov()
- Retorna a matriz de covariância implícita no modelo, se o modelo foi estimado. (numpy array)
- get_standard_errors()
- Lê os erros padrão da matriz de covariância implícita e das médias implícitas.
Retorna:
loadings_se (numpy array) – Os erros padrões para os cargas fatoriais.
error_vars_se (numpy array) – Os erros padrões para as variâncias de erros. - transform(X)
- Lê as pontuações para os fatores do novo conjunto de dados.
Parâmetros: X (tipo array, shape (n_amostras, n_características)) – Os dados a serem pontuados usando o modelo fatorial ajustado.
Retorna: pontuações – As variáveis latentes de X (um numpy array, shape (n_amostras, n_componentes)) - loadings
- (tipo array) – Especificação de cargas fatoriais.
error_vars (array-like) – Especificação de variância do erro
factor_covs (tipo array) – Especificação da covariância do fator.
factor_names (lista de str ou None) – uma lista de nomes de fatores, se disponível. Default: None.
variable_names (lista de str ou None) – Uma lista de nomes de variáveis, se disponível. Default: None. - loadings
- Especificação das cargas fatoriais. (Tipo: numpy array)
- error_vars
- Especificação da variância de erros. (Tipo: numpy array)
- factor_covs
- Especificação do fator de covariância. (Tipo: numpy array)
- n_factors
- Número de fatores. (Tipo: int).
- n_variables
- Número de variáveis. (Tipo: int).
- n_lower_diag
- Número de elementos no array factor_covs, igual à diagonal inferior da matriz de covariância fatorial. (Tipo: int).
- loadings_free
- Índices dos parâmetros de cargas fatoriais “livres”. (Tipo: numpy array)
- error_vars_free
- Índices dos parâmetros de variância de erros “livres”. (Tipo: numpy array)
- factor_covs_free
- Índices dos parâmetros de covariância de fator “livre”. (Tipo: numpy array)
- factor_names
- Lista dos nomes dos fatores, se disponível. (Tipo: lista de str ou None).
- variable_names
- Lista dos nomes das variáveis, se disponível. (Tipo: lista de str ou None).
- error_vars
- error_vars_free
- factor_covs
- factor_covs_free
- factor_names
- get_model_specification_as_dict()
- Retorna model_specification – O modelo de especificações, chaves e valores, como um dicionario (dict).
- copy()
- Retorna uma “deep copy” do objeto.
- loadings
- loadings_free
- n_factors
- n_lower_diag
- n_dtiables
- dtiable_names
- Parâmetros:
- X (tipo array) – O conjunto de dados será usado para a AFC.
specification (tipo array or None) – Array com os detalhes das cargas.
Se specification = None a matriz será criada supondo-se que todas as variáveis carregam em todos os fatores. Default: None. - Retorna:
- Objeto modelo de especificação, ModelSpecification.
- Exceção levantada:
- ValueError se especificação não está no formato esperado.
- Parâmetros:
- X (tipo array) – O conjunto de dados será usado para a AFC.
specification (tipo array or None) – Dicionário com os detalhes das cargas. Se None a matriz será criada supondo-se que todas as variáveis carregam em todos os fatores. Defaults = None. - Retorna: Objeto modelo de especificação, ModelSpecification.
- Exceção levantada: ValueError se especificação não está no formato esperado.
- method
- (str, opcional). Métodos de rotação disponíveis: Default: ‘varimax’.
- varimax (rotação ortogonal),
- promax (oblíqua),
- oblimin (oblíqua),
- oblimax (ortogonal),
- quartimin (oblíqua),
- quartimax (ortogonal),
- equamax (ortogonal),
- geomin_obl (oblíqua),
- geomin_ort (ortogonal).
- normalize
- (bool ou None, opcional) – Informa se uma normalização de Kaiser e de-normalização devem ser efetuadas antes e após a rotação. Usada para as rotações varimax e promax. Se None o default para promax é False, default para varimax é True. Default: None.
- power
- (int, opcional) – Potência das gargas de promax (menos 1). Geralmente na faixa entre 2 e 4. Default: 4.
- kappa
- (int, opcional) – Valor kappa para o objetivo equamax. Ignorado se método não for ‘equamax’. Default: 0.
- gamma
- (int, opcional) – Nível gamma para o objetivo ‘oblimin’. Ignorado se método não for ‘oblimin’. Default: 0.
- delta
- (float, opcional) – Nível delta level para o objetivo ‘geomin’. Ignorado se método não for ‘geomin_*’. Default: 0.01.
- max_iter
- (int, opcional) – Número máximo de iterações. Usado para método ‘varimax’ e rotações oblíquas. Default: 1000.
- tol
- (float, opcional) – Limite (threshold) de convergência. Usado para método ‘varimax’ e rotações oblíquas. Default: 1e-5.
- loadings_
- A matriz de carregamentos. (Tipo: numpy array, shape (n_características, n_fatores)
- rotation_
- psi_
- fit(X, y=None)
- Computa o fator de rotação model_specification – O modelo de especificações, chaves e valores, como um dicionario (dict).
- Parâmetros
- X (tipo array) – A matriz (n_características, n_fatores) de cargas fatoriais
y (não utilizado) - Retorna
- self
- fit_transform(X, y=None)
- Computa o fator de rotação e retorna a nova matriz de cargas fatoriais.
- Parâmetros
- X (tipo array) – A matriz (n_características, n_fatores) de cargas fatoriais
y (não utilizado) - Retorna
- loadings_, a matriz (n_características, n_fatores) de cargas fatoriais (numpy array)
- Erro levantado
- ValueError – se o método não está na lista de métodos aceitáveis.
- Biggs, Jeremy: Factor Analyser Documentation, acessado em dezembro de 2020.
Testes de Bartlett e KMO
factor_analyzer.factor_analyzer.calculate_bartlett_sphericity(x)
Testa a hipótese de que a matriz de correlação é igual à matriz identidade (o que significa que não há correlação entre as variáveis).
factor_analyzer.factor_analyzer.calculate_kmo(x)
Calcula o critério de Kaiser-Meyer-Olkin para cada fator individual e para o conjunto fatores. Essa estatística representa o grau com que cada variável observada pode ser predita, sem erro, pelas demais variáveis. Na maior parte dos casos KMO < 0.6 é considerado inadequado.
Análise Fatorial Confirmatória
Módulo factor_analyzer.confirmatory_factor_analyzer
class
factor_analyzer.confirmatory_factor_analyzer.ConfirmatoryFactorAnalyzer(specification=None,
n_obs=None, is_cov_matrix=False, bounds=None, max_iter=200,
tol=None, impute='median', disp=True)
A classe ConfirmatoryFactorAnalyzer ajusta um modelo de análise fatorial confirmatória usando o modelo de máxima verosimelhança (maximum likelihood).
class
factor_analyzer.confirmatory_factor_analyzer.ModelSpecification(loadings, n_factors, n_variables,
factor_names=None, variable_names=None)
Uma classe para encapsular a especificação do modelo para a análise confirmatória. Esta classe contém várias propriedades de especificação que são usadas no procedimento AFC.
Analisador de especificação de modelo
class factor_analyzer.confirmatory_factor_analyzer.ModelSpecificationParser
Uma classe para gerar a especificação do modelo para Análise Fatorial Confirmatória. Inclui dois métodos estáticos para gerar o objeto ModelSpecification a partir de um dicionário ou de um array numpy.
static parse_model_specification_from_array(X, specification=None)
Gera a especificação do modelo a partir de um array. As colunas devem corresponder aos fatores e as linhas às variáveis. Se este método for usado para criar a ModelSpecification nenhum nome de fator ou nome de variável serão adicionadoa como propriedades desse objeto.
static parse_model_specification_from_dict(X, specification=None)
Gere a especificação do modelo a partir de um dicionário. As chaves no dicionário devem ser os nomes dos fatores e os valores devem ser os nomes das características (features). Se esse método for usado para criar uma ModelSpecification os nomes dos fatores e das variáveis serão adicionados como propriedades a esse objeto.
Módulo factor_analyzer.rotator
Classe para executar diversas rotações nas matrizes de cargas fatoriais. Os métodos de rotação listados abaixo estão disponíveis tanto para FactorAnalyzer quanto para Rotator.
class
factor_analyzer.rotator.Rotator(method='varimax', normalize=True, power=4,
kappa=0, gamma=0, delta=0.01, max_iter=500, tol=1e-05)
Matriz de rotação. (Tipo: numpy array, shape (n_fatores, n_fatores))
Matriz de correlações fatoriais. Existe apenas se a rotação é oblíqua. (Tipo: numpy array ou None)