SQL (Structured Query Language) é uma linguagem de programação de uso específico utilizada para consultar, extrair e gerenciar bancos de dados relacionais. Pandas é uma biblioteca do Python especializada para o tratamento e análise de dados estruturados, incluindo uma gama de formas de extrair dados.
Esse artigo faz uma comparação entre as consultas feitas a dataframes do pandas e as consultas SQL, explorando similaridades e diferenças entre os dois sistemas. Ele serve para descrever as funcionalidades de busca e edição do pandas e pode ser particularmente útil para aqueles que conhecem SQL e pretendem usar o pandas (ou vice-versa).
Para realizar os experimentos abaixo usamos o Jupyter Notebook, um aplicativo que roda dentro de um navegador, que pode ser facilmente instalado e permite a reprodução se todo o código aqui descrito. Você pode ler mais sobre Jupyter Notebook e Linguagem de Consultas SQL nesse site.
Esse texto é baseado em parte do manual do pandas e expandido. Ele usa um conjunto de dados baixados do github renomeado aqui para dfGorjeta. Nomes e valores dos campos foram traduzidos para o português.
# importar as bibliotecas necessárias import pandas as pd import numpy as np url = "https://raw.github.com/pandas-dev/pandas/master/pandas/tests/io/data/csv/tips.csv" dfGorjeta = pd.read_csv(url) dfGorjeta.head()
| total_bill | tip | sex | smoker | day | time | size | |
|---|---|---|---|---|---|---|---|
| 0 | 16.99 | 1.01 | Female | No | Sun | Dinner | 2 |
| 1 | 10.34 | 1.66 | Male | No | Sun | Dinner | 3 |
| 2 | 21.01 | 3.50 | Male | No | Sun | Dinner | 3 |
| 3 | 23.68 | 3.31 | Male | No | Sun | Dinner | 2 |
| 4 | 24.59 | 3.61 | Female | No | Sun | Dinner | 4 |
Para efeito de testar os comandos do dataframe vamos alterar os nomes dos campos e traduzir os conteúdos dos dados. Para descobrir quais são os valores dos campos, sem repetições, transformamos as séries em sets, uma vez que valores de um set (conjunto) não se repetem.
print(set(dfGorjeta["sexo"])) print(set(dfGorjeta["fumante"])) print(set(dfGorjeta["dia"])) print(set(dfGorjeta["hora"]))
{‘No’, ‘Yes’}
{‘Sat’, ‘Sun’, ‘Fri’, ‘Thur’}
{‘Lunch’, ‘Dinner’}

No código seguinte alteramos os nomes de campos e traduzimos o conteúdo. A sintaxe da operação de edição do dataframe será discutida mais tarde no artigo:
# muda os nomes dos campos
dfGorjeta.rename(columns={"total_bill":"valor_conta", "tip":"gorjeta",
"smoker":"fumante", "sex":"sexo","day":"dia",
"time":"hora","size":"pessoas"}, inplace=True)
# traduzindo os valores dos campos:
dfGorjeta.loc[dfGorjeta["fumante"] == "No", "fumante"] = "não"
dfGorjeta.loc[dfGorjeta["fumante"] == "Yes", "fumante"] = "sim"
dfGorjeta.loc[dfGorjeta["sexo"] == "Female", "sexo"] = "mulher"
dfGorjeta.loc[dfGorjeta["sexo"] == "Male", "sexo"] = "homem"
dfGorjeta.loc[dfGorjeta["hora"] == "Dinner", "hora"] = "jantar"
dfGorjeta.loc[dfGorjeta["hora"] == "Lunch", "hora"] = "almoço"
dfGorjeta.loc[dfGorjeta["dia"] == "Fri", "dia"] = "sex"
dfGorjeta.loc[dfGorjeta["dia"] == "Sat", "dia"] = "sab"
dfGorjeta.loc[dfGorjeta["dia"] == "Sun", "dia"] = "dom"
dfGorjeta.loc[dfGorjeta["dia"] == "Thur", "dia"] = "qui"
# Temos agora o seguinte dataframe
dfGorjeta
| valor_conta | gorjeta | sexo | fumante | dia | hora | pessoas | |
|---|---|---|---|---|---|---|---|
| 0 | 16.99 | 1.01 | mulher | não | dom | jantar | 2 |
| 1 | 10.34 | 1.66 | homem | não | dom | jantar | 3 |
| 2 | 21.01 | 3.50 | homem | não | dom | jantar | 3 |
| 3 | 23.68 | 3.31 | homem | não | dom | jantar | 2 |
| 4 | 24.59 | 3.61 | mulher | não | dom | jantar | 4 |
| … | … | … | … | … | … | … | … |
| 239 | 29.03 | 5.92 | homem | não | sab | jantar | 3 |
| 240 | 27.18 | 2.00 | mulher | sim | sab | jantar | 2 |
| 241 | 22.67 | 2.00 | homem | sim | sab | jantar | 2 |
| 242 | 17.82 | 1.75 | homem | não | sab | jantar | 2 |
| 243 | 18.78 | 3.00 | mulher | não | qui | jantar | 2 |
As consultas SQL realizadas a seguir pressupõe a existência de um banco de dados com o mesmo nome, a mesma estrutura e dados que o dataframe dfGorjetas.
SELECT
 Nas consultas
Nas consultas SQL as seleções são feitas com uma lista de nomes de campos que se deseja retornar, separados por vírgula, ou através do atalho * (asterisco) para selecionar todas as colunas. No pandas a seleção de colunas é feita passando-se uma lista de nomes de campos para o DataFrame. Uma chamada ao dataframe sem uma lista de nomes de colunas resulta no retorno de todas as colunas, da mesma forma que usar * no SQL.
–– sql: consulta (query) usando select SELECT valor_conta, gorjeta, fumante, hora FROM dfGorjeta LIMIT 5;
# pandas: dfGorjeta[["valor_conta", "gorjeta", "hora"]].head()
| valor_conta | gorjeta | hora | |
|---|---|---|---|
| 0 | 16.99 | 1.01 | jantar |
| 1 | 10.34 | 1.66 | jantar |
| 2 | 21.01 | 3.50 | jantar |
| 3 | 23.68 | 3.31 | jantar |
| 4 | 24.59 | 3.61 | jantar |
O método head(n) limita o retorno do dataframe às n primeiras linhas. n = 5 é o default. Para listar as últimas linhas usamos tail(n). Linhas também podem ser selecionadas por chamadas ao sei indice.
# Para acessar as últimas linhas do dataframe podemos usar # dfGorjeta[["valor_conta", "gorjeta", "hora"]].tail() # selecionando linhas por meio de seu índice. dfGorjeta.iloc[[1,239,243]]
| valor_conta | gorjeta | sexo | fumante | dia | hora | pessoas | |
|---|---|---|---|---|---|---|---|
| 1 | 10.34 | 1.66 | homem | não | dom | jantar | 3 |
| 239 | 29.03 | 5.92 | homem | não | sab | jantar | 3 |
| 243 | 18.78 | 3.00 | mulher | não | qui | jantar | 2 |
Os dataframes possuem a propriedade shape que contém sua dimensionalidade. No nosso caso temos
dfGorjeta.shape
o que significa que são 244 linhas em 7 campos.
No SQL você pode retornar uma coluna resultado de um cálculo usando elementos de outras colunas. No pandas podemos usar o método assign() para inserir uma coluna calculada:
–– sql: SELECT *, gorjeta/valor_conta*100 as percentual FROM dfGorjeta LIMIT 4;
# pandas: método assign() dfGorjeta.assign(percentual = dfGorjeta["gorjeta"] / dfGorjeta["valor_conta" *100]).head(4)
| valor_conta | gorjeta | sexo | fumante | dia | hora | pessoas | percentual | |
|---|---|---|---|---|---|---|---|---|
| 0 | 16.99 | 1.01 | mulher | não | dom | jantar | 2 | 5.944673 |
| 1 | 10.34 | 1.66 | homem | não | dom | jantar | 3 | 16.054159 |
| 2 | 21.01 | 3.50 | homem | não | dom | jantar | 3 | 16.658734 |
| 3 | 23.68 | 3.31 | homem | não | dom | jantar | 2 | 13.978041 |
Essa coluna é retornada mas não fica anexada ao dataframe. Para anexar uma coluna ao dataframe podemos atribuir o resultado do cálculo a uma nova coluna:
dfGorjeta["percentual"] = dfGorjeta["gorjeta"] / dfGorjeta["valor_conta"] * 100
print("Nessa estapa temos as colunas:\n", dfGorjeta.columns)
# Vamos apagar a coluna recém criada para manter a simplicidade da tabela
dfGorjeta.drop(["percentual"], axis=1, inplace=True)
Index([‘valor_conta’, ‘gorjeta’, ‘sexo’, ‘fumante’, ‘dia’, ‘hora’, ‘pessoas’, ‘percentual’],
dtype=’object’)
WHERE

Filtragem de dados em consultas SQL são feitas através da cláusula WHERE. DataFrames podem ser filtrados de várias formas diferentes. O indexamento com valores booleanos é provavelmente o mais simples:
–– cláusula WHERE do sql SELECT * FROM dfGorjeta WHERE hora = "jantar" LIMIT 5;
# filtragem por indexamento no pandas dfGorjeta[dfGorjeta["hora"] == "jantar"].head(5)
| valor_conta | gorjeta | sexo | fumante | dia | hora | pessoas | |
|---|---|---|---|---|---|---|---|
| 0 | 16.99 | 1.01 | mulher | não | dom | jantar | 2 |
| 1 | 10.34 | 1.66 | homem | não | dom | jantar | 3 |
| 2 | 21.01 | 3.50 | homem | não | dom | jantar | 3 |
| 3 | 23.68 | 3.31 | homem | não | dom | jantar | 2 |
| 4 | 24.59 | 3.61 | mulher | não | dom | jantar | 4 |
A consulta acima funciona da seguinte forma:
# is_jantar é uma série contendo True e False (True para jantares, False para almoços)
is_jantar = dfGorjeta["hora"] == "jantar"
# usamos display para exibir a contagem de falsos/verdadeiros
display("Quantos jantares/almoços:", is_jantar.value_counts())
# para negar a série inteira, invertendo True ↔ False usamos ~ (til)
# a linha abaixo imprime o número de almoços na tabela
print("A lista contém %d almoços" % dfGorjeta[~is_jantar]["hora"].count())
# também podemos obter a lista das entradas que não correspondem a "jantar" usando
# dfGorjeta[dfGorjeta["hora"] != "jantar"]
True 176
False 68
Name: hora, dtype: int64A lista contém 68 almoços
Quando essa série é passada para o dataframe apenas as linhas correspondentes à True são retornados. A última consulta é equivalente à dfGorjeta[~is_jantar].head().
No SQL podemos procurar por partes de uma string com a cláusula LIKE. No pandas transformamos o campo dfGorjeta["sexo"]em uma string que possui o método startswith("string").
–– sql: SELECT TOP 2 sexo, valor_conta FROM dfGorjeta WHERE sexo LIKE 'ho%';
dfGorjeta.loc[dfGorjeta['sexo'].str.startswith('ho'),['sexo','valor_conta']].head(2)
que retorna as 2 primeiras linhas em que o campo sexo começa com o texto “ho”.
Também podemos procurar por campos que estão incluidos em um conjunto de valores:
–– sql:
SELECT * FROM dfGorjeta WHERE dia IN ('sab', 'dom');
dfGorjeta.loc[dfGorjeta['dia'].isin(["dom", "sab"])]
que retorna todas as linhas em que o campo dia é “dom” ou “sab”.
Assim como se pode usar operadores lógicos AND e OR nas consultas SQL para inserir múltiplas condições, o mesmo pode ser feito com dataframes usando | (OR) e & (AND). Por ex., para listar as gorjetas com valor superior à $5.00 dadas em jantares:
–– SQL: múltiplas condições em WHERE SELECT * FROM dfGorjeta WHERE hora = 'jantar' AND gorjeta > 6.00;
# no pandas dfGorjeta[(dfGorjeta["hora"] == "jantar") & (dfGorjeta["gorjeta"] > 6.00)]
| valor_conta | gorjeta | sexo | fumante | dia | hora | pessoas | |
|---|---|---|---|---|---|---|---|
| 23 | 39.42 | 7.58 | homem | não | sab | jantar | 4 |
| 59 | 48.27 | 6.73 | homem | não | sab | jantar | 4 |
| 170 | 50.81 | 10.00 | homem | sim | sab | jantar | 3 |
| 183 | 23.17 | 6.50 | homem | sim | dom | jantar | 4 |
| 212 | 48.33 | 9.00 | homem | não | sab | jantar | 4 |
| 214 | 28.17 | 6.50 | mulher | sim | sab | jantar | 3 |
Podemos obter uma lista dos dados correspondentes a gorjetas dadas por grupos com 5 ou mais pessoas ou com contas de valor acima de $45.00, limitada aos 4 primeiros registros:
–– SQL: SELECT * FROM dfGorjeta WHERE pessoas >= 5 OR valor_conta > 45 LIMIT 4;
# pandas dfGorjeta[(dfGorjeta["pessoas"] >= 5) | (dfGorjeta["valor_conta"] > 45)].head(4)
| valor_conta | gorjeta | sexo | fumante | dia | hora | pessoas | |
|---|---|---|---|---|---|---|---|
| 59 | 48.27 | 6.73 | homem | não | sab | jantar | 4 |
| 125 | 29.80 | 4.20 | mulher | não | qui | almoço | 6 |
| 141 | 34.30 | 6.70 | homem | não | qui | almoço | 6 |
| 142 | 41.19 | 5.00 | homem | não | qui | almoço | 5 |
 Dados ausentes são representados por
Dados ausentes são representados por NULL no, uma marca especial para indicar que um valor não existe no banco de dados. Nos dataframes do pandas o mesmo papel é desempenhado por NaN (Not a Number). Esses marcadores podem surgir, por ex., na leitura de um arquivo csv (valores separados por vírgulas) quando um valor está ausente ou não é um valor numérico em uma coluna de números. Para verificar o comportamento do pandas com NaN criamos um dataframe com valores ausentes. Verificações de nulos é feita com os métodos notna() e isna().
frame = pd.DataFrame({"col1": ["A", "B", np.NaN, "C", "D"], "col2": ["F", np.NaN, "G", "H", "I"]})
frame
| col1 | col2 | |
|---|---|---|
| 0 | A | F |
| 1 | B | NaN |
| 2 | NaN | G |
| 3 | C | H |
| 4 | D | I |
Se temos um banco de dados SQLcom essa estrutura e conteúdo podemos extrair as linhas onde col2 é NULL usando a consulta:
–– sql SELECT * FROM frame WHERE col2 IS NULL;
# no case do pandas usamos frame[frame["col2"].isna()]
| col1 | col2 | |
|---|---|---|
| 1 | B | NaN |
De forma análoga, podemos extrair as linhas para as quais col1 não é NULL. No pandas usamos notna().
–– sql SELECT * FROM frame WHERE col1 IS NOT NULL;
# pandas: linhas em que col1 não é nula frame[frame["col1"].notna()]
| col1 | col2 | |
|---|---|---|
| 0 | A | F |
| 1 | B | NaN |
| 3 | C | H |
| 4 | D | I |
GROUP BY

No SQL consultas com agrupamentos são feitas usando-se as operações GROUP BY. No pandas existe o método groupby() que tipicamente particiona o conjunto de dados em grupos e aplica alguma função (em geral de agregamento), combinando depois os grupos resultantes.
Um exemplo comum é o de particionar os dados em grupos menores e contar os elementos desses grupos. Voltando ao nosso dataframe dfGorjeta podemos consultar quantas gorjetas foram dadas por grupos de cada sexo:
–– sql SELECT sexo, count(*) FROM dfGorjeta GROUP BY sexo;
# o equivalente em pandas seria
dfGorjeta.groupby("sexo").size()
mulher 87
homem 157
dtype: int64
O resultado é uma series cujos valores podem ser retornados por seu nome de index ou pelo número desse indice.
print("A lista contém %d homens" % dfGorjeta.groupby("sexo").size()[0])
print("\t\t e %d mulheres" % dfGorjeta.groupby("sexo").size()["mulher"])
e 87 mulheres
É possível aplicar o método count() para cada coluna, individualmente:
dfGorjeta.groupby("sexo").count()
| valor_conta | gorjeta | fumante | almoço | hora | pessoas | |
|---|---|---|---|---|---|---|
| sexo | ||||||
| mulher | 87 | 87 | 87 | 87 | 87 | 87 |
| homem | 157 | 157 | 157 | 157 | 157 | 157 |
Observe que no código do pandas usamos size() e não count(). Isso foi feito porque o método count() é aplicado sobre cada coluna e retorna tantos valores quantas colunas existem, com valores não null.
Também se pode aplicar o método count() para uma coluna específica:
# para contar valores em uma única coluna primeiro ela é selecionada, depois contada
dfGorjeta.groupby("sexo")["valor_conta"].count()
mulher 87
homem 157
Name: valor_conta, dtype: int64
Existem diversas funções de agregamento. São elas:

| função | descrição |
|---|---|
| mean() | calcula médias para cada grupo |
| sum() | soma dos valores do grupo |
| size() | *tamanhos dos grupos |
| count() | número de registros no grupo |
| std() | desvio padrão dos grupos |
| var() | variância dos grupos |
| sem() | erro padrão da média dos grupos |
| describe() | gera estatísticas descritivas |
| first() | primeiro valor no grupo |
| last() | último valor no grupo |
| nth() | n-ésimo valor (ou subconjunto se n for uma lista) |
| min() | valor mínimo no grupo |
| max() | valor máximo no grupo |
* A função size() retorna o número de linhas em uma serie e o número de linhas × colunas em dataframes.
Para obter um resumo estatístico relativo ao campo gorjeta, agrupado pelo campo sexo podemos usar:
dfGorjeta.groupby("sexo")["gorjeta"].describe()
| count | mean | std | min | 25% | 50% | 75% | max | |
|---|---|---|---|---|---|---|---|---|
| sexo | ||||||||
| homem | 157.0 | 3.089618 | 1.489102 | 1.0 | 2.0 | 3.00 | 3.76 | 10.0 |
| mulher | 87.0 | 2.833448 | 1.159495 | 1.0 | 2.0 | 2.75 | 3.50 | 6.5 |
Múltiplas funções podem ser aplicadas de uma vez. Suponha que queremos determinar como os valores das gorjetas variam por dia da semana. O método agg() (de agregar) permite que se passe um dicionário para o dataframe agrupado, indicando que função deve ser aplicada a cada coluna.
–– sql (agrupe os dados por dia, calcule a média para cada dia e o número de entradas contadas) SELECT dia, AVG(gorjeta), COUNT(*) FROM dfGorjeta GROUP BY dia;
# na pandas, use mean no campo gorjeta, size no campo dia
dfGorjeta.groupby("dia").agg({"gorjeta": np.mean, "dia": np.size})
| gorjeta | dia | |
|---|---|---|
| dia | ||
| dom | 3.255132 | 76 |
| qui | 2.771452 | 62 |
| sab | 2.993103 | 87 |
| sex | 2.734737 | 19 |
Também é possível realizar o agrupamento por mais de uma coluna. Para fazer isso passamos uma lista de colunas para o método groupby().
–– agrupe primeiro por "fumante", depois por "dia" –– realize a contagem dos registros e a média das gorjetas SELECT fumante, dia, COUNT(*), AVG(gorjeta) FROM dfGorjeta GROUP BY fumante, dia;
# no pandas
dfGorjeta.groupby(["fumante", "dia"]).agg({"gorjeta": [np.size, np.mean]})
| gorjeta | |||
|---|---|---|---|
| size | mean | ||
| fumante | dia | ||
| não | dom | 57.0 | 3.167895 |
| qui | 45.0 | 2.673778 | |
| sab | 45.0 | 3.102889 | |
| sex | 4.0 | 2.812500 | |
| sim | dom | 19.0 | 3.516842 |
| qui | 17.0 | 3.030000 | |
| sab | 42.0 | 2.875476 | |
| sex | 15.0 | 2.714000 | |
JOIN
 No SQL tabelas podem ser juntadas ou agrupadas através da cláusula
No SQL tabelas podem ser juntadas ou agrupadas através da cláusula JOIN. Junções podem ser LEFT, RIGHT, INNER, FULL. No pandas se usa os métodos join() ou merge(). Por defaultjoin() juntará os DataFrames por seus índices. Cada método tem parâmetros que permitem escolher o tipo da junção (LEFT, RIGHT, INNER, FULL), ou as colunas que devem ser juntadas (por nome das colunas ou índices). [Linguagem de Consultas SQL]
# para os exercícios que se seguem criamos os dataframes
df1 = pd.DataFrame({"key": ["A", "B", "C", "D"], "value": [11, 12, 13, 14]})
df2 = pd.DataFrame({"key": ["B", "D", "D", "E"], "value": [21, 22, 23, 24]})
# para exibir esses dataframes com formatação usamos display()
display(df1)
display(df2)
| key | value | |
|---|---|---|
| 0 | A | 11 |
| 1 | B | 12 |
| 2 | C | 13 |
| 3 | D | 14 |
| key | value | |
|---|---|---|
| 0 | B | 21 |
| 1 | D | 22 |
| 2 | D | 23 |
| 3 | E | 24 |
Como antes supomos a existência de duas tabelas de dados sql como as mesmas estruturas e dados para considerarmos as várias formas de JOINs.
INNER JOIN
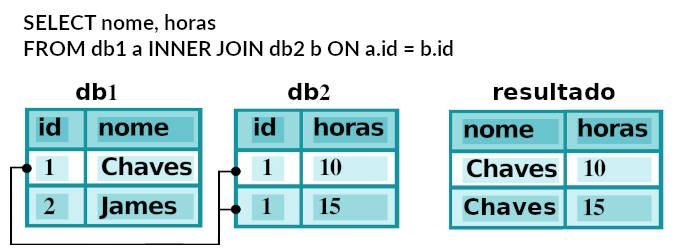
–– junção das duas tabelas ligadas por suas chaves - key SELECT * FROM df1 INNER JOIN df2 ON df1.key = df2.key;
# por default merge() faz um INNER JOIN pd.merge(df1, df2, on="key")
| key | value_x | value_y | |
|---|---|---|---|
| 0 | B | 12 | 21 |
| 1 | D | 14 | 22 |
| 2 | D | 14 | 23 |
O método merge() também oferece parâmetros para que sejam feitas junções de uma coluna de um dataframe com o índice de outro dataframe. Para ver isso vamos criar outro dataframe a partir de df2, usando o campo key como índice.
# novo dataframe tem campo "key" como índice
df2_indice = df2.set_index("key")
display(df2_indice)
pd.merge(df1, df2_indice, left_on="key", right_index=True)
| value | |
|---|---|
| key | |
| B | 21 |
| D | 22 |
| D | 23 |
| E | 24 |
| key | value_x | value_y | |
|---|---|---|---|
| 1 | B | 12 | 21 |
| 3 | D | 14 | 22 |
| 3 | D | 14 | 23 |
LEFT OUTER JOIN
A junção LEFT OUTER JOIN recupera todos as campos à esquerda, existindo ou não uma linha correspondente à direita. O parâmetro how="left" é o equivalente no pandas.
–– sql: recupera todos os valores de df1 existindo ou não correspondente em df2 SELECT * FROM df1 LEFT OUTER JOIN df2 ON df1.key = df2.key;
# pandas: how="left" equivale a LEFT OUTER JOIN pd.merge(df1, df2, on="key", how="left")
| key | value_x | value_y | |
|---|---|---|---|
| 0 | A | 11 | NaN |
| 1 | B | 12 | 21 |
| 2 | C | 13 | NaN |
| 3 | D | 14 | 22 |
| 4 | D | 14 | 23 |
Observe que df2 não possui campos com key = "A" ou key = "C" e, por isso o dataframe resultante tem NaN nessas entradas. key = "A". Como df2 tem 2 linhas para key = "D" a linha aparece duplicada para essa key em df1.
RIGHT JOIN
A junção RIGH OUTER JOIN recupera todos as campos à direita, existindo ou não uma linha correspondente à esquerda. O parâmetro how="right" é o equivalente no pandas.
–– sql: recupera todos os registros em df2 SELECT * FROM df1 RIGHT OUTER JOIN df2 ON df1.key = df2.key;
# pandas: how="right" equivale a RIGHT OUTER JOIN pd.merge(df1, df2, on="key", how="right")
| key | value_x | value_y | |
|---|---|---|---|
| 0 | B | 12 | 21 |
| 1 | D | 14 | 22 |
| 2 | D | 14 | 23 |
| 3 | E | NaN | 24 |
FULL JOIN
A junção FULL OUTER JOIN recupera todos as campos à direita ou à esquerda, representando como NaN os valores ausentes em uma ou outra. Todos as linhas das duas tabelas são retornadas com junção onde a campo key existe em ambas. O parâmetro how="outer" é o equivalente no pandas. Observe que nem todos os gerenciadores de bancos de dados permitem essa operação.
–– sql: retorna todos os registros em ambas as tabelas SELECT * FROM df1 FULL OUTER JOIN df2 ON df1.key = df2.key;
# pandas: how="outer" é o equivalente em dataframes pd.merge(df1, df2, on="key", how="outer")
| key | value_x | value_y | |
|---|---|---|---|
| 0 | A | 11 | NaN |
| 1 | B | 12 | 21 |
| 2 | C | 13 | NaN |
| 3 | D | 14 | 22 |
| 4 | D | 14 | 23 |
| 5 | E | NaN | 24 |

UNION
Para os exemplos seguintes definimos mais 2 dataframes:
df3 = pd.DataFrame({"cidade": ["Rio de Janeiro", "São Paulo", "Belo Horizonte"], "nota": [1, 2, 3]})
df4 = pd.DataFrame({"cidade": ["Rio de Janeiro", "Curitiba", "Brasília"], "nota": [1, 4, 5]})
No SQL a clásula UNION ALL é usada para juntar as linhas retornadas em dois (ou mais) instruções de SELECT. Linhas duplicadas são mantidas. O mesmo efeito pode ser conseguido no pandas usando-se o método concat().
–– sql: UNION ALL SELECT city, rank FROM df3 UNION ALL SELECT cidade, nota FROM df4;
# pandas: concat pd.concat([df3, df4])
| cidade | nota | |
|---|---|---|
| 0 | Rio de Janeiro | 1 |
| 1 | São Paulo | 2 |
| 2 | Belo Horizonte | 3 |
| 0 | Rio de Janeiro | 1 |
| 1 | Curitiba | 14 |
| 2 | Brasília | 5 |
No SQL a cláusula UNION tem o mesmo efeito que UNION ALL mas remove as linhas duplicadas. No pandas isso pode ser conseguido se fazendo a conactenação concat() seguida de drop_duplicates().
–– SQL UNION SELECT city, rank FROM df1 UNION SELECT city, rank FROM df2; –– o registro duplicado no Rio de Janeiro fica excluído
# pandas: concat() seguido de drop_duplicates() pd.concat([df1, df2]).drop_duplicates()
| cidade | nota | |
|---|---|---|
| 0 | Rio de Janeiro | 1 |
| 1 | São Paulo | 2 |
| 2 | Belo Horizonte | 3 |
| 1 | Curitiba | 14 |
| 2 | Brasília | 5 |
Outras funções analíticas e de agregamento
Para os próximos exemplos vamos retornar ao nosso dataframe dfGorjeta: para listar as 5 gorjetas mais altas, no MySQL (a sintaxe varia de um para outro gerenciador).
–– MySQL: retorna todos os campos em ordem decrescente, 5 linhas SELECT * FROM dfGorjeta ORDER BY gorjeta DESC LIMIT 10 OFFSET 5;
# pandas: seleciona 15 maiores e exibe as 10 de menor valor dfGorjeta.nlargest(15, columns="gorjeta").tail(10)
| valor_conta | gorjeta | sexo | fumante | dia | hora | pessoas | |
|---|---|---|---|---|---|---|---|
| 183 | 23.17 | 6.50 | homem | sim | Dom | jantar | 4 |
| 214 | 28.17 | 6.50 | mulher | sim | sab | jantar | 3 |
| 47 | 32.40 | 6.00 | homem | não | Dom | jantar | 4 |
| 239 | 29.03 | 5.92 | homem | não | sab | jantar | 3 |
| 88 | 24.71 | 5.85 | homem | não | Thur | almoço | 2 |
| 181 | 23.33 | 5.65 | homem | sim | Dom | jantar | 2 |
| 44 | 30.40 | 5.60 | homem | não | Dom | jantar | 4 |
| 52 | 34.81 | 5.20 | mulher | não | Dom | jantar | 4 |
| 85 | 34.83 | 5.17 | mulher | não | Thur | almoço | 4 |
| 211 | 25.89 | 5.16 | homem | sim | sab | jantar | 4 |
UPDATE
Há muitas formas de alterar um valor em um campo de um dataframe. Por exemplo, abaixo realizamos uma alteração em todos os valores de gorjeta sempre que gorjeta < 2.
–– sql: em todas as linhas duplique a gorjeta se gorjeta for menor que 1.1 UPDATE dfGorjeta SET gorjeta = gorjeta*2 WHERE gorjeta < 1.1;
# pandas: o mesmo resultado pode ser obtido da aseguinte forma # dfGorjeta.loc[dfGorjeta["gorjeta"] < 1.1, "gorjeta"] *= 2
Para explicar com mais detalhes o funcionamento deste código, armazenamos abaixo a lista dos índices das linhas de gorjetas mais baixas e exibimos essas linhas. Em seguida multiplicamos apenas as gorjetas dessas linhas por 2 e examinamos o resultado:
indices = dfGorjeta[dfGorjeta["gorjeta"] < 1.1].index
print("Índices de gorjetas < 1.1:", indices)
display("Lista de gorjetas < 1.1", dfGorjeta.iloc[indices])
# multiplica essas gorjetas por 2
dfGorjeta.loc[dfGorjeta["gorjeta"] < 1.1, "gorjeta"] *= 2
# lista as mesmas linhas após a operação
display("Gorjetas após a operação:", dfGorjeta.iloc[indices])
Index([0, 67, 92, 111, 236], dtype=’int64′)
‘Lista de gorjetas < 1.1’
| valor_conta | gorjeta | sexo | fumante | dia | hora | pessoas | |
|---|---|---|---|---|---|---|---|
| 0 | 16.99 | 1.01 | mulher | não | dom | jantar | 2 |
| 67 | 3.07 | 1.00 | mulher | sim | sab | jantar | 1 |
| 92 | 5.75 | 1.00 | mulher | sim | sex | jantar | 2 |
| 111 | 7.25 | 1.00 | mulher | não | sab | jantar | 1 |
| 236 | 12.60 | 1.00 | homem | sim | sab | jantar | 2 |
‘Gorjetas após a operação:’
| valor_conta | gorjeta | sexo | fumante | dia | hora | pessoas | |
|---|---|---|---|---|---|---|---|
| 0 | 16.99 | 2.02 | mulher | não | dom | jantar | 2 |
| 67 | 3.07 | 2.00 | mulher | sim | sab | jantar | 1 |
| 92 | 5.75 | 2.00 | mulher | sim | sex | jantar | 2 |
| 111 | 7.25 | 2.00 | mulher | não | sab | jantar | 1 |
| 236 | 12.60 | 2.00 | homem | sim | sab | jantar | 2 |
–– sql: alterar um campo de uma linha específica (supondo a existência de um campo id) UPDATE dfGorjeta SET sexo = 'NI' WHERE id = 239
# para alterar o campo sexo para 'NI' (não informado) dfGorjeta.loc[239, 'sexo'] ='NI'
DELETE
 Existem muitas formas de se excluir linhas de um dataframe mas é comum a prática de selecionar as linhas que devem ser mantidas e copiar para um novo dataframe.
Existem muitas formas de se excluir linhas de um dataframe mas é comum a prática de selecionar as linhas que devem ser mantidas e copiar para um novo dataframe.
DELETE FROM dfGorjeta WHERE gorjeta > 9;
# pandas: como novo dataframe tem o mesmo nome do original, o antigo é sobrescrito e perdido dfTop = dfGorjeta.loc[dfGorjeta["gorjeta"] > 9] dfTop
| valor_conta | gorjeta | sexo | fumante | dia | hora | pessoas | |
|---|---|---|---|---|---|---|---|
| 170 | 50.81 | 10.0 | homem | sim | sab | jantar | 3 |
Também é possível apagar linhas usando seu índice:
# apagar linha com index = 4, inplace para substituir o dataframe dfGorjeta.drop(index=4, inplace=True) # apagar linhas com index = 0 até 3 dfGorjeta.drop(index=[0, 1, 2, 3], inplace=True) dfGorjeta.head()
| valor_conta | gorjeta | sexo | fumante | dia | hora | pessoas | |
|---|---|---|---|---|---|---|---|
| 5 | 25.29 | 4.71 | homem | não | dom | jantar | 4 |
| 6 | 8.77 | 12.00 | homem | não | dom | jantar | 2 |
| 7 | 26.88 | 3.12 | homem | não | dom | jantar | 4 |
| 8 | 15.04 | 1.96 | homem | não | dom | jantar | 2 |
| 9 | 14.78 | 3.23 | homem | não | dom | jantar | 2 |
Bibliografia
- McKinney, Wes: Python for Data Analysis, Data Wrangling with Pandas, NumPy,and IPython
O’Reilly Media, 2018. - Pandas: página oficial, acessada em janeiro de 2021.